微積分
外觀
歡迎來到華夏公益教科書的
微積分
| 一位華夏公益教科書使用者建議將 微積分課程 合併到本書中。 在 討論頁面 上討論是否應該進行此合併。 |
本華夏公益教科書旨在成為一本高質量的 微積分 教科書,使用者可以透過它掌握這門學科。涵蓋了極限、微分和積分等標準主題,以及其他幾個主題。請在您認為有必要的地方進行 貢獻。您只需透過對您認為評分不當的書籍的各個部分進行評分來幫助我們!


積分
[edit | edit source]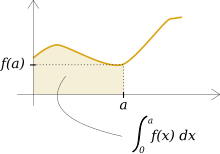
積分基礎
[edit | edit source]積分技巧
[edit | edit source]
- 加速度函式 a(t);
- 加速度的積分是速度函式 v(t);
- 速度的積分是距離函式 s(t)。
積分應用
[edit | edit source]
引數方程
[edit | edit source]極座標方程
[edit | edit source]數列和級數
[edit | edit source]數列
[edit | edit source]級數和檢驗方法
[edit | edit source]

7.11 反函式定理,隱函式定理 (可選)
- 舊: 二重積分
- Lester R. Ford, Sr. & Jr. (1963) 微積分, McGraw-Hill via HathiTrust
- w:Mellen W. Haskell (1895) 關於引入雙曲函式的概念 美國數學會通報 1(6):155–9.
