微積分/面積

介紹

在微積分中，求兩條曲線（通常由兩個顯式函式給出）之間的面積通常很有用。

一般來說，求兩條曲線之間面積的規則是

$A=A_{\rm {top}}-A_{\rm {bottom}}$ 或

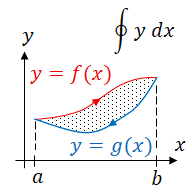
如果 f(x) 是上方的函式，g(x) 是下方的函式

$A=\int \limits _{a}^{b}{\bigl (}f(x)-g(x){\bigr )}dx$

無論函式是在第一象限還是不在第一象限，這都是正確的。

兩條曲線之間的面積

假設我們有兩個函式 $y_{1}=f(x)$ 和 $y_{2}=g(x)$，我們想找到它們在區間 $[a,b]$ 上的面積。還需要假設對於區間 $[a,b]$ 上的所有 $x$，有 $f(x)\geq g(x)$。首先，我們將區間 $[a,b]$ 分割成 $n$ 個等長的子區間，每個子區間的長度為 $\Delta x={\frac {b-a}{n}}$。接下來，在每個子區間中選擇一個點，記為 $x_{i}^{*}$。現在，我們可以為每個區間‘建立’一個矩形。在點 $x_{i}*$處，每個矩形的高度為 $f(x_{i}^{*})-g(x_{i}^{*})$，寬度為 $\Delta x$。因此，每個矩形的面積為 ${\bigl [}f(x_{i}^{*})-g(x_{i}^{*}){\bigr ]}\Delta x$。兩個曲線之間的面積 $A$ 的一個近似值為：

$A:=\sum _{i=1}^{n}{\Big [}f(x_{i}^{*})-g(x_{i}^{*}){\Big ]}\Delta x$ .

現在，我們取 $n$ 趨於無窮大的極限，得到：

$A=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big [}f(x_{i}^{*})-g(x_{i}^{*}){\Big ]}\Delta x$

這給出了精確的面積。回顧定積分的定義，我們注意到

$A=\int \limits _{a}^{b}{\bigl (}f(x)-g(x){\bigr )}dx$ .

求兩條曲線之間面積的公式有時被稱為關於 *x* 軸的積分，因為用於逼近面積的矩形的底邊平行於 *x* 軸。當兩個函式的形式為 $y_{1}=f(x)$ 和 $y_{2}=g(x)$ 時，該公式最為有用。然而，有時人們會發現相對於 *y* 軸積分更簡單。當相對於 *x* 軸積分會導致需要計算多個積分時，就會出現這種情況。這些函式的形式為 $x_{1}=f(y)$ 和 $x_{2}=g(y)$ 在區間 $[c,d]$ 上。注意 $[c,d]$ 是 $y$ 的值。這種情況的推導完全相同。與之前類似，我們將假設 $f(y)\geq g(y)$ 對於 $[c,d]$ 上的所有 $y$ 成立。現在，如前所述，我們可以將區間分成 $n$ 個子區間，並建立矩形來逼近 $f(y)$ 和 $g(y)$ 之間的面積。可能需要想象每個矩形的“寬度”， $\Delta y$ ，平行於 *y* 軸，而“高度”， $f(y_{i}^{*})-g(y_{i}^{*})$ 在點 $y_{i}^{*}$ 處，平行於 *x* 軸。從上面的工作中我們可以推斷出，面積的 *近似值*， $A$ ，在兩條曲線之間是

$A:=\sum _{i=1}^{n}{\Big [}f(y_{i}^{*})-g(y_{i}^{*}){\Big ]}\Delta y$ .

如同之前，我們將$n$視為趨近於無窮大，得到

$A=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big [}f(y_{i}^{*})-g(y_{i}^{*}){\Big ]}\Delta y$ ,

這不過是一個定積分，因此

$A=\int \limits _{c}^{d}{\bigl (}f(y)-g(y){\bigr )}dy$ .

無論函式的形式如何，我們都使用相同的公式。