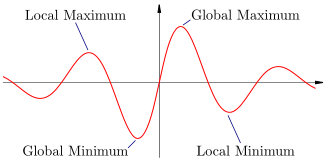
 四種類型的極值。
四種類型的極值。
最大值和最小值分別是函式達到最高值或最低值的點。 極值(表示最大值或最小值)有兩種型別:全域性和區域性,有時分別稱為“絕對”和“相對”。 全域性最大值是指在函式的整個範圍內取最大值的點,而全域性最小值是指在函式的整個範圍內取最小值的點。 另一方面,區域性極值是指函式在緊鄰區域內的最大值或最小值。
在許多情況下,極值看起來像函式圖形上的山峰或碗底。 全域性極值也總是區域性極值,因為它是在函式的整個範圍內取得最大值或最小值,因此也是其鄰近範圍內的最大值或最小值。 函式也可以沒有極值,無論是全域性還是區域性:  就是一個簡單的例子。
就是一個簡單的例子。
在任何極值處,圖形的斜率必然為 0(或未定義,例如  ),因為圖形必須在極值處停止上升或下降,並開始向相反方向移動。 因此,極值也常稱為駐點或拐點。 因此,函式的一階導數在極值處等於 0。 如果圖形有一個或多個這些駐點,可以透過將一階導數設為 0 並求解所得方程的根來找到這些點。
),因為圖形必須在極值處停止上升或下降,並開始向相反方向移動。 因此,極值也常稱為駐點或拐點。 因此,函式的一階導數在極值處等於 0。 如果圖形有一個或多個這些駐點,可以透過將一階導數設為 0 並求解所得方程的根來找到這些點。
 函式
函式  ,它在點
,它在點  處包含一個鞍點。
處包含一個鞍點。
但是,斜率為零並不保證是最大值或最小值:還存在第三類稱為鞍點的駐點。 考慮函式

導數為

在  處的斜率為 0。 我們有一個斜率為 0 的點,但雖然這使其成為一個駐點,但這並不意味著它是最大值或最小值。 檢視函式圖形你會發現
處的斜率為 0。 我們有一個斜率為 0 的點,但雖然這使其成為一個駐點,但這並不意味著它是最大值或最小值。 檢視函式圖形你會發現  既不是最大值也不是最小值,它只是一個函式變平的點。 真正的極值要求一階導數的符號發生變化。 這很有道理 - 你必須上升(正斜率)到最大值並下降(負斜率)從最大值。 在上升和下降之間,在光滑的曲線上,會出現一個斜率為零的點 - 最大值。 最小值將表現出類似的性質,只是順序相反。
既不是最大值也不是最小值,它只是一個函式變平的點。 真正的極值要求一階導數的符號發生變化。 這很有道理 - 你必須上升(正斜率)到最大值並下降(負斜率)從最大值。 在上升和下降之間,在光滑的曲線上,會出現一個斜率為零的點 - 最大值。 最小值將表現出類似的性質,只是順序相反。
 好的(B 和 C,綠色)和不好的(D 和 E,藍色)點,用於檢查以對極值(A,黑色)進行分類。 不好的點會導致對 A 作為最小值的錯誤分類。
好的(B 和 C,綠色)和不好的(D 和 E,藍色)點,用於檢查以對極值(A,黑色)進行分類。 不好的點會導致對 A 作為最小值的錯誤分類。
這導致了一個對駐點進行分類的簡單方法 - 將 x 值稍微左移和右移代入函式的導數。 如果結果的符號相反,那麼它就是一個真正的最大值/最小值。 你也可以使用這些斜率來確定它是最大值還是最小值:左邊的斜率對於最大值是正的,對於最小值是負的。 但是,你必須謹慎使用這種方法,因為如果你選擇的點離極值太遠,你可能會在另一個極值的另一側取點,從而錯誤地對該點進行分類。
對駐點進行分類的一種更嚴格的方法稱為極值測試或二階導數測試。 如前所述,一階導數的符號必須發生變化,駐點才能成為真正的極值。 現在,函式的二階導數告訴我們一階導數的變化率。 因此,如果二階導數在駐點處為正,則梯度正在增加。 事實上,它是一個駐點本身意味著這隻能是一個最小值。 相反,如果二階導數在該點處為負,則它是一個最大值。
現在,如果二階導數為 0,我們遇到了問題。 它可能是一個拐點,也可能仍然是一個極值。 下面的例子說明了這兩種情況 - 所有這些情況在所討論的駐點處都有二階導數等於 0
 在
在  處有一個拐點
處有一個拐點 在
在  處有一個最小值
處有一個最小值 在
在  處取得最大值。
處取得最大值。
然而,這不是一個無法解決的問題。我們需要做的是繼續求導,直到在第  次導數處,在駐點獲得非零結果。
次導數處,在駐點獲得非零結果。

如果  為奇數,則駐點為真正的極值點。如果第
為奇數,則駐點為真正的極值點。如果第  次導數為正,則為最小值;如果第
次導數為正,則為最小值;如果第  次導數為負,則為最大值。如果
次導數為負,則為最大值。如果  為偶數,則駐點為拐點。
為偶數,則駐點為拐點。
例如,讓我們考慮函式

現在我們求導,直到在駐點  處獲得非零結果(假設我們已經像往常一樣找到了這個點)。
處獲得非零結果(假設我們已經像往常一樣找到了這個點)。




因此, 為 4,所以
為 4,所以  為 3。這是一個奇數,四階導數為負,因此我們有一個最大值。請注意,所給出的方法都不能告訴您這是一個全域性極值還是區域性極值。為此,您需要將函式設定為極值的高度,然後尋找其他根。
為 3。這是一個奇數,四階導數為負,因此我們有一個最大值。請注意,所給出的方法都不能告訴您這是一個全域性極值還是區域性極值。為此,您需要將函式設定為極值的高度,然後尋找其他根。
臨界點 是函式導數為 0 或未定義的點。假設我們想要在一個閉區間上找到一個連續函式的最大值或最小值。該函式在該區間上的極值將出現在一個或多個臨界點和/或一個或兩個端點處。我們可以用反證法證明這一點。假設函式  在區間
在區間  的點
的點  處取得最大值,其中函式的導數已定義且不為
處取得最大值,其中函式的導數已定義且不為  。如果導數為正,則比
。如果導數為正,則比  略大的
略大的  值將導致函式增加。由於
值將導致函式增加。由於  不是端點,其中至少一些值在
不是端點,其中至少一些值在 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 中。但這與
中。但這與  是
是  在
在 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上的最大值的假設相矛盾。類似地,如果導數為負,則比
上的最大值的假設相矛盾。類似地,如果導數為負,則比  略小的
略小的  值將導致函式增加。由於
值將導致函式增加。由於  不是端點,其中至少一些值在
不是端點,其中至少一些值在 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 中。這與
中。這與  是
是  在
在 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 上的最大值的假設相矛盾。對於最小值也可以進行類似的論證。
上的最大值的假設相矛盾。對於最小值也可以進行類似的論證。
考慮區間 ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) 上的函式
上的函式  。不受限制的函式
。不受限制的函式  沒有最大值或最小值。然而,在區間
沒有最大值或最小值。然而,在區間 ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) 上,很明顯最小值將是
上,很明顯最小值將是  ,出現在
,出現在  處,最大值將是
處,最大值將是  ,出現在
,出現在  處。由於不存在臨界點(
處。由於不存在臨界點( 存在且處處等於
存在且處處等於  ),極值必須出現在端點處。
),極值必須出現在端點處。
找到區間 ![{\displaystyle [-3,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a869f6f7ff84a95f888c6b8705e2465ba21960e) 上的函式
上的函式  的最大值和最小值。
的最大值和最小值。
首先找到函式導數的根


- 現在在所有臨界點和端點處評估函式,以找到極值。




- 由此可見,區間上的最小值為 -24,當
 時;區間上的最大值為
時;區間上的最大值為  ,當
,當  時。
時。
請參閱 "最佳化",瞭解這些原理的常見應用。




























![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)






![{\displaystyle [-3,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a869f6f7ff84a95f888c6b8705e2465ba21960e)









