微積分/最佳化

簡介

最佳化是微積分在現實世界中的應用之一。也許我們是一家比薩店，希望最大化利潤。也許我們有一塊平坦的硬紙板，我們需要用它製作體積最大的盒子。如何才能實現這個目標呢？

這需要用到最大值和最小值。我們知道，我們可以透過導數來找到最大值和最小值。因此，我們可以得出結論，微積分將成為最大化或最小化（統稱為“最佳化”）某個情況的有用工具。

通常，最佳化問題有一個約束條件，它會改變我們看待問題的方式。問題的措辭（無論多麼微妙）也會極大地改變我們看待問題的方式。約束條件是我們絕對不會改變的東西（例如，一般形狀，或者我們願意為整個操作支付的金額等等）。如果我們能夠識別出我們將要改變什麼以及我們將要求保持不變的東西，那麼我們就將開始解決問題。

如何解決

為了完成最佳化問題，應該按照以下步驟進行。

1. 寫出問題中給出的必要公式和其他資訊。
   • 問題應該有一個你可以控制的變數和一個你想要最大化/最小化的變數。
   • 你找到的公式可能包含額外的變數。根據問題的解決方式，這些變數可能會被替換掉，或者可以忽略（稍後將進行解釋）。
2. 將公式組合起來，使你想要最大化/最小化的變數位於等式的左側，所有其他變數位於右側。
3. 對公式求導。如果你的方程包含多個變數，可以選擇任何變數進行求導，只要它不是你控制的變數（即，選擇你無法從公式中消除的變數）。
   • 請注意，在求導過程中，如果你遇到一個你沒有選擇的變數，將其視為一個數字並應用必要的求導規則。在這種情況下，不要將其視為變數。
4. 將求導後的公式設為 0，並求解你控制的變數。
5. 你在這裡得到的值就是你的答案。如果你得到另一個公式，這意味著你的答案取決於其他變數，這通常是你最初遇到這種情況時，問題所要求的。

這種演算法之所以有效，是因為幾個數學定理，而這些定理你可能在解決這些問題時並不需要知道。通常給出的問題在數學上都很簡單（換句話說，沒有很多情況需要測試）。但是，如果你想了解，它們是這樣的

• 導數為 0 的點，要麼是全域性最大值或最小值，要麼是區域性最大值或最小值。通常問題會傾向於在沒有太多困難的情況下回答這個問題（例如，總是正數）。

示例

體積示例

一個盒子製造商想要製作一個表面積為 100 平方英寸的封閉盒子，該盒子具有正方形底座，但側面為矩形。將這種材料彎成盒子後，可以形成的最大體積是多少？

• 寫出已知的公式和資訊

$A_{base}=x^{2}$

$A_{side}=x\cdot h$

$A_{total}=2x^{2}+4x\cdot h=100$

$V=l\cdot w\cdot h=x^{2}\cdot h$

• 將變數 $h$ 寫成體積方程中 $x$ 的表示式。

$2x^{2}+4xh=100$

$x^{2}+2xh=50$

$2xh=50-x^{2}$

$h={\frac {50-x^{2}}{2x}}$

${\begin{aligned}V&=\left(x^{2}\right)\left({\frac {50-x^{2}}{2x}}\right)\\&={\frac {50x-x^{3}}{2}}\end{aligned}}$

• 為了最大化體積，求體積方程的導數

${\frac {dV}{dx}}={\frac {50-3x^{2}}{2}}$

• 令${\frac {dV}{dx}}=0$，並解出$x$

${\frac {50-3x^{2}}{2}}=0$

$50-3x^{2}=0$

$3x^{2}=50$

$x=\pm {\frac {\sqrt {50}}{\sqrt {3}}}$

• 將$x$值代入體積方程並化簡

${\begin{aligned}V&={\frac {1}{2}}\left[50{\sqrt {\frac {50}{3}}}-\left({\sqrt {\frac {50}{3}}}\right)^{3}\right]\\&=68.04138174...\end{aligned}}$

答案：$V_{max}=68.04138174...$

體積示例二

想要用一塊邊長為$\alpha$的正方形錫片製作一個最大容積的無蓋箱子，方法是在角上剪去相同的正方形，然後折起錫片形成箱子的側面。剪去的正方形的邊長應該為多少？

如果我們將切口正方形的邊長稱為$x$，那麼摺疊盒底部的每條邊都是$\alpha -2x$，高度是$x$。因此，體積函式是$V(x)=x(\alpha -2x)^{2}=x(\alpha ^{2}-4\alpha x+4x^{2})=\alpha ^{2}x-4\alpha x^{2}+4x^{3}$。我們必須透過對體積函式求導並將其設定為0來最佳化體積。由於它不改變，$\alpha$被視為常數，而不是變數。

$V(x)=\alpha ^{2}x-4\alpha x^{2}+4x^{3}$

${\begin{aligned}0&=V'(x)=\alpha ^{2}-8\alpha x+12x^{2}\\&=12x^{2}-8\alpha x+\alpha ^{2}\end{aligned}}$

現在我們可以使用二次公式來求解$x$

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

${\begin{aligned}x&={\frac {-(-8\alpha )\pm {\sqrt {(-8\alpha )^{2}-4(12)(\alpha ^{2})}}}{2(12)}}\\&={\frac {8\alpha \pm {\sqrt {64\alpha ^{2}-48\alpha ^{2}}}}{24}}\\&={\frac {8\alpha \pm {\sqrt {16\alpha ^{2}}}}{24}}\\&={\frac {8\alpha \pm 4\alpha }{24}}\end{aligned}}$

$x={\frac {\alpha }{6}},{\frac {\alpha }{2}}$

我們拒絕$x={\frac {\alpha }{2}}$，因為它是最小值（它會導致底邊長度$\alpha -2x$為0，使體積為0）。

因此，答案是$x={\frac {\alpha }{6}}$。

體積示例 III

需要一個圓柱形罐子來盛放$1.024{\text{ L}}$ 的液體。確定能使製造指定體積罐子所需的材料量最小的尺寸。

這是一個經典的最佳化問題。問題是我們沒有任何指定的尺寸。幸運的是，我們給出了國際單位制，因此我們可以相應地寫出我們給出的內容。

• 轉換因子：$1{\text{ L}}=1000{\text{ cm}}^{3}$。這意味著透過量綱分析（或基本代數）：$1.024{\text{ L}}=1024{\text{ cm}}^{3}$。請記住，這是體積！
• 圓柱體積：$V=\pi r^{2}h$
• 圓柱表面積：$S=2\pi rh+2\pi r^{2}$

請記住我們要最小化什麼：“製造指定體積罐子所需的材料量”。這意味著表面積需要最小化！不幸的是，我們有兩個變數（它不是常數）。幸運的是，我們可以使用體積來寫$h$ 關於$r$ 的表示式。

$1024{\text{ cm}}^{3}=\pi r^{2}h$

$\Rightarrow {\frac {1024{\text{ cm}}^{3}}{\pi {r{\text{ cm}}}^{2}}}={\frac {1024}{\pi r^{2}}}{\text{ cm}}=h$

我們可以將此資訊代入表面積公式並最小化（將一階導數設為零）

$S(r)=2\pi r\left({\frac {1024}{\pi r^{2}}}\right)+2\pi r^{2}$。消除$\pi$ 和$r$。

$\Rightarrow S(r)=2\cdot {\frac {1024}{r}}+2\pi r^{2}$ 將一階導數設為零。

${\begin{aligned}\Rightarrow 0=S'(r)&={\frac {d}{dr}}\left({\frac {2048}{r}}+2\pi r^{2}\right)\\&={\frac {d}{dr}}\left({\frac {2048}{r}}\right)+{\frac {d}{dr}}\left(2\pi r^{2}\right)\\&={\frac {d}{dr}}\left(2048\cdot {r}^{-1}\right)+2\pi {\frac {d}{dr}}\left(r^{2}\right)\\&=2048\cdot {\frac {d}{dr}}\left({r}^{-1}\right)+2\pi \left(2r\right)\\&=2048\cdot (-1){r}^{-2}+4\pi r\\&=-{\frac {2048}{{r}^{2}}}+4\pi r\\&={\frac {4\pi r^{3}-2048}{{r}^{2}}}\end{aligned}}$

接下來要做的就是找到操作的臨界值。 這最終意味著讓分子等於零，並找到什麼值 $r$ 使分母等於零。 這是分子運算

$4\pi r^{3}-2048=0$

$\Leftrightarrow 4\pi r^{3}=2048$

$\Leftrightarrow r^{3}={\frac {2048}{4\pi }}={\frac {512}{\pi }}$

$\Leftrightarrow r={\sqrt[{3}]{\frac {512}{\pi }}}={\frac {8}{\sqrt[{3}]{\pi }}}\approx 5.4623$

這是分母的運算

${r}^{2}=0$

$r=\pm 0$

需要注意的是，我們並不關心其中一個臨界值是否等於零。這個問題要求我們找到使條件成立且最小化的值。雖然零確實最小化了建造罐頭所需的材料量，但如果我們不顯示一個罐頭，我們就無法建造罐頭。然而，如果我們被問及 $S(r)$ 的圖形，這個解就會很有趣。儘管如此，我們的最終答案不一定就是 $r\approx 5.4623{\text{ cm}}$ 和 $h\approx 10.9245{\text{ cm}}$。我們需要驗證我們找到的臨界值是否為正確答案。這時，我們需要將 $r\in \left(0,\,{\frac {8}{\sqrt[{3}]{\pi }}}\right)$ 和 $r\in \left({\frac {8}{\sqrt[{3}]{\pi }}},\,\infty \right)$ 的值代入一階導數。

對於 $r\in \left(0,\,{\frac {8}{\sqrt[{3}]{\pi }}}\right)$，令 $r=5$：$S'(5)={\frac {4\pi (5)^{3}-2048}{(5)^{2}}}<0$。對於 $r\in \left({\frac {8}{\sqrt[{3}]{\pi }}},\,\infty \right)$，令 $r=6$：$S'(6)={\frac {4\pi (6)^{3}-2048}{(6)^{2}}}>0$。

根據以上結果，很明顯 $r={\frac {8}{\sqrt[{3}]{\pi }}}$ 是一個最小化函式的值，同時允許我們建造罐頭。請記住，如果你沒有證明我們找到的值是極小值，那麼這個值也可能是極大值。想象一下，如果情況是這樣的，我們建議公司生產一個最大化材料用量的罐頭。潛在的數百萬美元的材料成本將抵消最佳利潤。無論哪種情況，我們都找到了答案。

答案：半徑為 $5.4623{\text{ cm}}$，高度為 $10.9245{\text{ cm}}$。

銷售示例

一家小型零售商可以以 $n$ 的數量售出一件產品，其收入為 $r(n)=8.1n$，成本為 $c(n)=n^{3}-7n^{2}+18n$，所有金額均以千計。它需要售出多少單位才能使其利潤最大化？

零售商的利潤由等式 $p(n)=r(n)-c(n)$ 定義，它表示產生的淨收入。問題要求利潤最大化，或者上述等式的最大值。如前所述，圖形的最大值和最小值是在圖形的斜率等於零時找到的。要找到斜率，需要找到感興趣的函式的導數——這裡，$p(n)$。利用減法法則 $p'(n)=r'(n)-c'(n)$

$p(n)=r(n)-c(n)$

$p'(n)={\frac {d}{dn}}[8.1n]-{\frac {d}{dn}}\left[n^{3}-7n^{2}+18n\right]=-3n^{2}+14n-9.9$

因此，當 $-3n^{2}+14n-9.9=0$ 時，利潤將被最大化或最小化。使用 二次公式 求解根，得到 $n=0.869,3.798$。要找到這兩個中的哪一個是最大值和最小值，可以對函式進行測試

$p(0.869)=-3.97321,p(3.798)=8.58802$

因為我們只考慮所有 $n\geq 0$ 的函式（即，你不可能有 $n=-5$ 個單位），唯一可能成為最小值或最大值的點是上面列出的這兩個點。為了證明 $3.798$ 實際上是一個最大值（以及該函式在這一點之後不保持恆定），檢查 $p'(n)$ 的符號在這一點上是否發生變化。

在這裡，它確實如此，並且對於大於$3.798$的$n$，$P'(n)$ 將繼續下降。這表明公司將在$n=3.798$ 處實現利潤最大化。銷售$3.798$ 個單位的零售商將獲得 $$8,588.02$ 的利潤。

然而，答案是$n=3.798$.

收入示例

最大化收入

一家小部件公司具有線性需求函式 $D(q)=-{\frac {1}{5}}q+10$，其中 $q$ 是運送給客戶的小部件（以百計）的公斤數。小部件應該以什麼價格出售才能使收入最大化？

公司的收入是透過將銷售數量乘以價格來計算的。由於$D(q)$ 是價格，而 $q$ 是銷售數量，$R(q)=q\cdot D(q)$。問題要求我們找到將數量最大化的價格。這意味著找到數量是第一個目標。最終目標是找到的價格。

我們的第一個目標是找到使收入最大化的數量。如果切線的斜率在某一點為零，並且該點周圍斜率的符號從正變為負，則收入函式將被最大化。這是透過求導數並應用一階導數檢驗來實現的。當收入函式分配$q$ 時，這將更容易

${\begin{aligned}R(q)&=q\cdot D(q)\\&=q\cdot \left(-{\frac {1}{5}}q+10\right)\\&=-{\frac {1}{5}}q^{2}+10q\end{aligned}}$

現在讓我們求一階導數

${\frac {d}{dq}}\left[R(q)\right]={\frac {d}{dq}}\left[-{\frac {1}{5}}q^{2}+10q\right]$

${\begin{aligned}R'(q)&={\frac {d}{dq}}\left[-{\frac {1}{5}}q^{2}\right]+{\frac {d}{dq}}\left[10q\right]\\&=-{\frac {1}{5}}{\frac {d}{dq}}\left[q^{2}\right]+10{\frac {d}{dq}}\left[q\right]\\&=-{\frac {1}{5}}\left[2q\right]+10\left[1\right]\\&=-{\frac {2}{5}}q+10\end{aligned}}$

將一階導數設為零以找到臨界值

$R'(q)=0=-{\frac {2}{5}}q+10$

$\Leftrightarrow -10=-{\frac {2}{5}}q$

$\Leftrightarrow 25=q$

請注意原始的收入函式。因為收入函式是一個二次函式，其 $q^{2}$ 項乘以小於 0 的因子，因此保證只有一個臨界值，並且它必須是最大值。基於微積分的方法只是證實了這一事實（使用一階導數檢驗）

對於任何 $q<25$，$R'(q)>0$。對於任何 $q>25$，$R'(q)<0$。因此，臨界值 $q=25$ 必須是最大值。

剩下的就是將這個域輸入到需求函式中，以找到小部件的售價。這是一個簡單的替換練習

${\begin{aligned}D(25)&=-{\frac {1}{5}}(25)+10\\&=-5+10\\&=5\end{aligned}}$

小部件應該以 $$5$ 的價格出售以使收入最大化。

函式到原點的距離

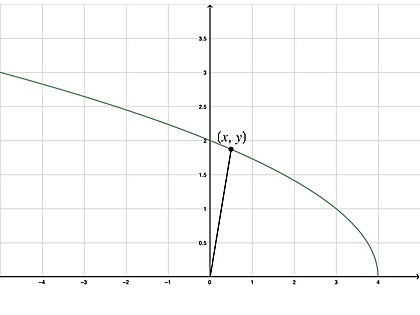
一個典型的最佳化問題，儘管有點抽象。

函式 $f(x)={\sqrt {4-x}}$ 在 $xy$ 平面上繪製。函式上的一個粒子應該停在函式的哪個點，使得該點到原點的直線距離最小化？

讓我們寫下所有可能需要記住的相關方程

• $D={\sqrt {\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}}$
• $y=f(x)$

最佳化問題的一個難點在於，大多數情況下我們處理的是兩個變數而不是一個變數。然而，主要思路和重點是將二元方程轉化為一元方程。這裡需要將變數聯絡起來。最好的方法是利用問題的設定來發揮優勢。

我們希望將函式保留在 $(x,y)$，並最小化到達原點的距離。這意味著我們設 $\left(x_{2},y_{2}\right)=(x,y)$。回顧一下，原點位於 $(0,0)$，所以 $\left(x_{1},y_{1}\right)=(0,0)$。有了這裡的所有資訊，讓我們用單變數 $x$ 來寫出距離函式。因為 $y=f(x)$

${\begin{aligned}D(x)&={\sqrt {\left(x-0\right)^{2}+\left(f(x)-0\right)^{2}}}\\&={\sqrt {x^{2}+\left({\sqrt {4-x}}\right)^{2}}}\\&={\sqrt {x^{2}+4-x}}\\&={\sqrt {x^{2}-x+4}}\end{aligned}}$

我們將展示兩種求導方法：標準方法和非標準方法。標準方法需要使用鏈式法則，讓我們演示一下這個過程。

標準方法

$D(x)={\sqrt {x^{2}-x+4}}$

$\Rightarrow {\frac {d}{dx}}\left[D(x)\right]={\frac {d}{dx}}\left({\sqrt {x^{2}-x+4}}\right)$

${\begin{aligned}\Rightarrow D'(x)&={\frac {d}{dx}}\left({\sqrt {x^{2}-x+4}}\right)&\left({\text{Recall the chain rule: }}{\frac {d}{dx}}\left[f\left(g(x)\right)\right]={\frac {df}{dg}}\cdot {\frac {dg}{dx}}\right)\\&={\frac {d}{dx}}\left(x^{2}-x+4\right)\cdot {\frac {df}{dg}}\left({\sqrt {x^{2}-x+4}}\right)\\&=\left(2x-1\right)\cdot {\frac {1}{2{\sqrt {x^{2}-x+4}}}}\\&={\frac {2x-1}{2{\sqrt {x^{2}-x+4}}}}\end{aligned}}$

現在我們有了距離公式的一階導數。為了最小化 $(x,y)$ 與原點之間的距離，我們將一階導數設為零。到目前為止，你應該知道為什麼要這樣做。

令 $D'(x)=0$.

${\frac {2x-1}{2{\sqrt {x^{2}-x+4}}}}=0$ 意味著分子為零。因此

令 $2x-1=0$.

$2x-1=0$

$\Leftrightarrow 2x=1$

$\Leftrightarrow x={\frac {1}{2}}$

回想一下，如果分母可以被設為零，那麼使之成立的 $x$ 值是一個臨界值。因此，令 $2{\sqrt {x^{2}-x+4}}=0$

$2{\sqrt {x^{2}-x+4}}=0$

$\Rightarrow {\sqrt {x^{2}-x+4}}=0$

$\Rightarrow x^{2}-x+4=0$

對於 $x$，不存在任何使上述方程成立的實際值。這可以透過行列式小於零來證明：$b^{2}-4ac<0$。因此，

唯一的臨界值為 $x={\frac {1}{2}}$。現在，你應該會想到我們需要使用一階導數測試

對於任何 $x<{\frac {1}{2}}$，$D'(x)<0$。對於任何 $x>{\frac {1}{2}}$，$D'(x)>0$。這意味著臨界值之前的函式在遞減，臨界值之後的函式在遞增。這說明臨界值處的函式為區域性最小值。

因此，$x$的值將使 $(x,y)$ 與原點之間的距離最小，值為 $x={\frac {1}{2}}$。

然而，你還沒有完成這個問題。你還需要找到粒子需要停止的函式點。這只是將 $x$ 代入函式 $f(x)$ 的問題。

${\begin{aligned}f\left({\frac {1}{2}}\right)&={\sqrt {4-\left({\frac {1}{2}}\right)}}\\&={\sqrt {{\frac {8}{2}}-{\frac {1}{2}}}}\\&={\sqrt {\frac {7}{2}}}\end{aligned}}$

大多數微積分課程的老師並不介意你將答案保留為 $\left({\frac {1}{2}},{\sqrt {\frac {7}{2}}}\right)$。然而，對於少數關心分母有理化的老師或考試機構，${\sqrt {\frac {7}{2}}}$ 的工作如下

${\begin{aligned}{\sqrt {\frac {7}{2}}}&={\frac {\sqrt {7}}{\sqrt {2}}}\\&={\frac {\sqrt {7}}{\sqrt {2}}}\cdot {\frac {\sqrt {2}}{\sqrt {2}}}\\&={\frac {{\sqrt {7}}\cdot {\sqrt {2}}}{2}}\\&={\frac {\sqrt {14}}{2}}\\\end{aligned}}$

這就是為什麼大多數老師不介意分母保留為平方根的原因；它會分散對微積分的注意力（雖然只是略微分散）。這讓我們得到了最終答案

為了使粒子到達原點的距離最小，粒子必須在 $\left({\frac {1}{2}},{\frac {\sqrt {14}}{2}}\right)$ 離開函式。 $\blacksquare$

非標準方法：隱式微分

由於除了隱式微分之外的任何計算都會導致與之前概述的相同過程，因此這裡只展示隱式微分。回想一下 $D(x)={\sqrt {x^{2}-x+4}}$。將兩邊平方得到以下函式

$\left[D(x)\right]^{2}=x^{2}-x+4$

對上述函式關於 $x$ 求導需要我們進行隱式微分（儘管這種微分被巧妙地掩蓋了）。下面的計算展示了這一過程

${\frac {d}{dx}}\left[\left(D(x)\right)^{2}\right]={\frac {d}{dx}}\left(x^{2}-x+4\right)$

${\begin{aligned}\Rightarrow 2D(x){\frac {dD}{dx}}&={\frac {d}{dx}}\left(x^{2}\right)-{\frac {d}{dx}}\left(x\right)+{\frac {d}{dx}}\left(4\right)\\&=2x-1+0\\\end{aligned}}$

$2D(x){\frac {dD}{dx}}=2x-1$

${\begin{aligned}\Leftrightarrow {\frac {dD}{dx}}&={\frac {2x-1}{2D(x)}}\\&={\frac {2x-1}{2{\sqrt {x^{2}-x+4}}}}\end{aligned}}$

請注意，上面的計算得出的結果與用標準方法求出的第一個導數相同，這意味著從這裡開始的計算將是相同的。有了這個，讓我們進入下一個問題。

最大化彎曲架子形成的矩形區域

這裡的問題是另一個問題的偽裝變體。

假設有一個函式 $f(x)=15\log(x)$ 描述了一個風格化貨架一部分的曲線。這條曲線在距離垂直牆壁水平方向 $100$ 釐米處結束。製造商希望這部分貨架的前表面有一個大的矩形凹槽，凹槽的左上角形成一個與貨架底部平行的水平部分。為了滿足製造商的要求，這個凹槽所形成的垂直牆壁距離貨架左側多遠？可以使用計算器進行計算。

這個問題看起來很奇怪。但實際上，這是一個經過偽裝的常見最佳化問題變種，即函式問題中形成的最大矩形區域。如果用這種思路來考慮問題，問題會變得更容易處理。畢竟，製造商想要的是最大化凹槽尺寸。他沒有詢問尺寸的體積，只是詢問在哪裡可以找到滿足要求的部分。

右側所示的影像實際上就是所形成的最大區域。然而，如果問題沒有提供影像（以及軸上的數字），那麼就無法進行近似。

令 $x$ 表示距離貨架左側的距離，令所形成的矩形的高度為 $y=f(x)$。這種構造意味著 $(100-x)$ 是矩形的長度，而高度是 $15\log(x)$。因此，面積函式為

$A(x)=15(100-x)\log(x)$

我們要找到該函式的最大值。讓我們求出面積函式的導數並令其等於零

$A(x)=15(100-x)\log(x)$

$\Rightarrow {\frac {d}{dx}}\left[A(x)\right]={\frac {d}{dx}}\left[15(100-x)\log(x)\right]$

${\begin{aligned}\Rightarrow A'(x)&=15{\frac {d}{dx}}\left((100-x)\log(x)\right)&\left({\text{Recall the product rule: }}{\frac {d}{dx}}\left[f(x)\cdot g(x)\right]=f\cdot {\frac {dg}{dx}}+g\cdot {\frac {df}{dx}}\right)\\&=15\left[(100-x)\cdot {\frac {d}{dx}}\left(\log(x)\right)+\log(x)\cdot {\frac {d}{dx}}\left(100-x\right)\right]\\&=15\left[{\frac {100-x}{x\ln(10)}}-\log(x)\right]\\&=15\left[{\frac {100-x}{x\ln(10)}}-{\frac {\ln(x)}{\ln(10)}}\right]&\left({\text{Multiply by }}{\frac {x}{x}}{\text{ to the right fraction.}}\right)\\&=15\left[{\frac {100-x}{x\ln(10)}}-{\frac {x\ln(x)}{x\ln(10)}}\right]\\&=15\left[{\frac {100-x-x\ln(x)}{x\ln(10)}}\right]=0\\\end{aligned}}$

然而，在找到一階導數後，很明顯，我們目前還不知道在這種特定情況下如何求解 $x$ 的值，因為我們還不知道 Lambert-W 函式。因此，現在可以使用圖形計算器（通常，許多老師希望在允許你使用計算器求解之前看到儘可能多的步驟）。如果沒有圖形計算器，可以使用 Desmos 或 Geogebra 或其他許多線上圖形計算器。

這些網站獲得的答案是 $x\approx 23.94721$ 或精確解 $x=e^{W(100e)-1}$。我們知道這也是我們正在尋找的最大值，因為導數函式在 $x<23.94721$ 時為正，但在之後變為負。對於那些好奇的人來說，最大面積是 $1573.44277$ 平方釐米。

答案：$x\approx 23.94721$

不同區域的速度

我們試圖找到的示意圖：到達目的地所需的最短距離 $\Lambda$。

根據費馬最小時間原理，光線以最短時間跨越最短距離（即，光線以最少浪費時間的方式傳播）。光波的速度定義為光速除以傳播介質的折射率，即 $v={\frac {c}{n}}$。假設一束光波穿過兩種材料，從 $n_{1}$ 開始，在 $n_{2}$ 結束，其中 $n_{1}<n_{2}$。入射角和折射角在右邊的圖中給出。光線穿過兩種不同材料之間的關係是什麼？

這看起來不像一個最佳化問題。實際上，看起來嘗試將其變成一個最佳化問題會不合常理。然而，這個物理學中的漂亮結果僅僅是透過將其變成一個最佳化問題而發現的巧妙發現。

讓我們寫下我們所知道的

• 入射點和材料變化之間的距離是 $\Upsilon$（圖中使用的是斜體大寫的upsilon）。
• 使傳播時間最短的距離是 $\Lambda$（圖中使用的是斜體大寫的lambda）。這意味著根據圖示，剩餘的水平距離是 $d-\Lambda$。
• 材料變化和折射材料末端之間的距離是 $\Gamma$（圖中使用的是斜體大寫的gamma）。

剩下的就是把所有東西拼湊起來了。我們想要找到光線傳播的距離。

• 入射光線傳播的距離是 ${\sqrt {(\Lambda )^{2}+(\Upsilon )^{2}}}$.
• 折射光線傳播的距離是 ${\sqrt {(d-\Lambda )^{2}+(\Gamma )^{2}}}$.

讓我們回顧一下我們所知道的。我們試圖操作 $\Lambda$ 使得傳播時間儘可能短，從而反映和模擬光線穿過兩種不同材料的方式。除 $\Lambda$ 以外的所有其他非函式項都是常數。由於我們試圖模擬光線穿過兩種不同材料所需的時間，因此我們應該操作距離使其模擬時間。

回想一下，速度是距離和時間的比值 $\left(v={\frac {D}{\Delta t}}\right)$，因此使用給定距離模擬光線傳播所需的時間，只需要進行一些重新排列即可。由於光線穿過兩種不同的材料，速度不同。設 $v_{1}>v_{2}$，其中 $v_{1}$ 是光線在折射率為 $n_{1}$ 的第一種材料中傳播的速度（$v_{2}$ 也是如此）。

• $t_{1}={\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}$
• $t_{2}={\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}$

光線穿過這兩種材料所需的時間以 $\Lambda$ 的函式形式給出，因此

• $T(\Lambda )=t_{1}+t_{2}={\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}+{\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}$

現在我們終於有了最佳化問題。我們想要最小化傳播時間。將 $T(\Lambda )$ 的一階導數設為零。記住，除了 $\Lambda$ 以外的所有其他項都是常數。

$T(\Lambda )={\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}+{\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}$

${\frac {d}{d\Lambda }}\left[T(\Lambda )\right]={\frac {d}{d\Lambda }}\left({\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}+{\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}\right)$

回顧我們想要解決的問題。我們不是要解出$\Lambda$；我們試圖對情況進行建模。如果我們確實需要解出$\Lambda$，那將是一場噩夢（我們甚至可以將其留作讀者的一個非平凡練習），但無論如何，我們可以開始對情況進行建模。首先，將負項移到另一邊

${\frac {1}{v_{1}}}\cdot \left({\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}\right)-{\frac {1}{v_{2}}}\cdot \left({\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}\right)=0$

${\frac {1}{v_{1}}}\cdot \left({\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}\right)={\frac {1}{v_{2}}}\cdot \left({\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}\right)$

該圖顯示了應用不同幾何特性後涉及的角度之間的關係。

接下來我們應該嘗試重寫表示式，以便清理那些分數（畢竟它們很嚇人，而且建模也不實用）。

我們可以在這裡使用三角函式來幫助我們。因為三角函式只是直角三角形比率的關係，所以這將是一個非常好的解決方案。

法線被定義為垂直於給定“表面”的線。由於距離$\Upsilon$平行於法線，因此它所產生的角度也是$90^{\circ }$。由於光傳播的水平距離$d$平行於“表面”，因此光線的入射角$\theta _{1}$，是距離$\Upsilon$和入射光向量$\mathbf {I}$之間的角度，並且光向量$\mathbf {I}$是橫截線，根據同位角定理，距離$\Upsilon$和入射光向量$\mathbf {I}$之間的角度也是$\theta _{1}$（參見圖的左上角以供參考）。

這種幾何推導的結果很簡單：我們找到了直角三角形的一部分的角度。因此，我們可以將距離寫成三角函式的等價形式

• $\sin(\theta _{1})={\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}$

我們可以用類似的邏輯來證明

• $\sin(\theta _{2})={\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}$

因此，我們可以將相關的方程式改寫成更易於管理和計算的形式，而無需測量比率。

${\frac {1}{v_{1}}}\cdot \left({\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}\right)={\frac {1}{v_{2}}}\cdot \left({\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}\right)$

$\Leftrightarrow {\frac {1}{v_{1}}}\cdot \sin(\theta _{1})={\frac {1}{v_{2}}}\sin(\theta _{2})$

我們實際上還沒有解決這個問題。儘管我們可能已經將兩個不同的光向量聯絡起來，但我們並沒有根據折射率對這種情況進行建模。這留下了最後兩個步驟。回顧一下，光線穿過折射率為 $n$ 的特定材料的速度為 $v={\frac {c}{n}}$。這等同於說 ${\frac {1}{v}}={\frac {n}{c}}$。由於速度與折射率有關，我們可以將上面的方程式改寫為

${\frac {n_{1}\cdot \sin(\theta _{1})}{c}}={\frac {n_{2}\cdot \sin(\theta _{2})}{c}}$

兩邊都乘以 $c$，我們終於找到了 *斯涅爾定律*

答案：$n_{1}\sin(\theta _{1})=n_{2}\sin(\theta _{2})$

請記住，這個結果仍然是一個導數。但是，我們允許根據微分方程對現實生活中的場景進行建模。有時，可能無法在沒有微分方程的情況下對情況進行建模。我們允許這樣寫我們的方程（物理學當然不在乎這裡）。最後，雖然這不是嚴格意義上的最佳化問題，但從這個角度思考使我們能夠獲得一個關於世界的良好規則（科學中的 *定律*）。我們證明了這種行為，所以光似乎將根據這個方程保持一致。實際上，這使我們能夠在 2003 年確認負折射率的存在（即使透過實驗觀察），並使我們能夠發現自旋波的性質。