微積分/一些重要定理

本節涵蓋了微分學中三個基本重要的定理：極值定理、羅爾定理和中值定理。它還討論了可導性和連續性之間的關係。

極值定理

極值的分類

我們從一些定義開始。

全域性最大值

函式$f$在閉區間$[a,b]$上的全域性最大值（也稱為絕對最大值）是某個值$f(c)$，使得對於所有$x\in [a,b]$，都有$f(c)\geq f(x)$。

全域性最小值

函式$f$在閉區間$[a,b]$上的全域性最小值（也稱為絕對最小值）是某個值$f(c)$，使得對於所有$x\in [a,b]$，都有$f(c)\leq f(x)$。

最大值和最小值統稱為極值。

極值定理

極值定理

如果$f$是在閉區間$[a,b]$上連續的函式，那麼$f$在$[a,b]$上既有全域性最小值，也有全域性最大值。假設$a,b$都是有限的。

極值定理是實分析中的一個基本結果，其證明超出了本文的範圍。但是，該定理的正確性使我們能夠討論閉區間上連續函式的最大值和最小值，而無需考慮它們是否存在。當處理不滿足定理前提的函式時，我們需要考慮這些問題。例如，無界函式$f(x)=x$根本沒有任何極值。如果$f(x)$被限制在半閉區間$[0,1)$上，則$f$在$x=0$處具有最小值0，但它沒有最大值，因為對於任何給定的值$c\in [0,1)$，總能找到$f(x)$更大的值，其中$x\in [0,1)$，例如透過形成$f(d)$，其中$d$是$c$與1的平均值。函式$g(x)={\frac {1}{x}}$在$x=0$處不連續。$g(x)$在圍繞$x=0$的任何閉區間內都沒有任何極值，因為當從左側接近0時函式是無界下降的，而當從右側接近0時函式是無界上升的。（事實上，函式在$x=0$處未定義。但是，如果將$g(0)$賦值為任意值，則該示例不受影響。)

極值定理是一個存在定理。它告訴我們，如果滿足某些條件，則全域性極值存在，但它沒有告訴我們如何找到它們。我們將在標題為極值和拐點的部分中討論如何確定連續函式的極值。

羅爾定理

羅爾定理

如果函式$f(x)$

• 在閉區間$[a,b]$上連續
• 在開區間$(a,b)$上可導
• $f(a)=f(b)$

那麼至少存在一個數$c\in (a,b)$，使得

$f'(c)=0$

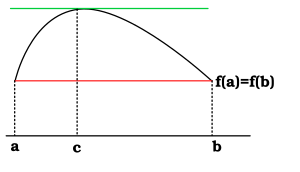
羅爾定理在證明均值定理中非常重要。直觀地說，它表示如果有一個函式在區間內處處連續，並且該區間的邊界點處的函式值相同，並且如果該函式在區間內處處可導（除了可能在端點處），那麼該函式在區間內部至少存在一個地方斜率為零。

羅爾定理的證明

如果$f$在$[a,b]$上是常數，則對於每個$x\in [a,b]$，$f'(x)=0$，因此定理成立。因此，在接下來的討論中，我們假設$f$在$[a,b]$上不是常數。

由於$f$滿足極值定理的條件，$f$必須在$[a,b]$上取得其最大值和最小值。由於$f$在$[a,b]$上不是常數，端點不可能同時是最大值和最小值。因此，至少存在一個極值在$(a,b)$內。我們可以假設，不失一般性，這個極值是一個最大值，因為如果它是一個最小值，我們可以考慮函式$-f$。令$f(c)$，其中$c\in (a,b)$為最大值。剩下的需要證明的是$f'(c)=0$。

根據導數的定義，$f'(c)=\lim _{h\to 0}{\frac {f(c+h)-f(c)}{h}}$。將$h=x-c$代入，這等價於$\lim _{x\to c}{\frac {f(x)-f(c)}{x-c}}$。注意，對於所有$x\in [a,b]$，$f(x)-f(c)\leq 0$，因為$f(c)$是$[a,b]$上的最大值。

$\lim _{x\to c^{-}}{\frac {f(x)-f(c)}{x-c}}\geq 0$，因為分子非正，分母為負。

$\lim _{x\to c^{+}}{\frac {f(x)-f(c)}{x-c}}\leq 0$，因為分子非正，分母為正。

由於函式在$c$處可導，因此左右極限必須相等，所以$\lim _{x\to c}{\frac {f(x)-f(c)}{x-c}}=0=f'(c)$。

練習

1. 證明羅爾定理適用於函式$f(x)=x^{2}-3x$的x截距之間。

均值定理

均值定理

如果函式$f(x)$

• 在閉區間$[a,b]$上連續
• 在開區間$(a,b)$上可導

則存在至少一個$c\in (a,b)$ 使得

$f'(c)={\frac {f(b)-f(a)}{b-a}}$

均值定理是微積分中的一個重要定理。它基本上說，對於定義在區間上的可微函式，區間上存在某個點的瞬時斜率等於該區間的平均斜率。請注意，當$f(a)=f(b)$ 時，羅爾定理是均值定理的特例。

為了證明均值定理，我們將證明一個更一般的陳述，均值定理是其特例。該陳述是柯西均值定理，也稱為擴充套件均值定理。

柯西均值定理

柯西均值定理

如果$f(x),g(x)$ 是

• 在閉區間$[a,b]$上連續
• 在開區間$(a,b)$上可導

則存在一個數$c\in (a,b)$ 使得

$f'(c)(g(b)-g(a))=g'(c)(f(b)-f(a))$

如果$g(b)\neq g(a)$ 且$g'(c)\neq 0$ ，則這等價於

${\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}$

為了證明柯西中值定理，考慮函式

$h(x)=f(x)(g(b)-g(a))-g(x)(f(b)-f(a))-f(a)g(b)+f(b)g(a)$

由於 $f$ 和 $g$ 在 $[a,b]$ 上連續並在 $(a,b)$ 上可微，因此 $h$ 也是如此。

$h'(x)=f'(x)(g(b)-g(a))-g'(x)(f(b)-f(a))$

由於 $h(a)=h(b)$（參見練習），羅爾定理告訴我們存在某個數 $c\in (a,b)$ 使得 $h'(c)=0$。這意味著

$f'(c)(g(b)-g(a))=g'(c)(f(b)-f(a))$

這就是需要證明的。

練習

2. 證明 $h(a)=h(b)$，其中 $h(x)$ 是在柯西中值定理證明中定義的函式。

3. 證明均值定理可由柯西均值定理推導得出。

4. 求滿足函式$f(x)=x^{3}$在端點$x=0$和$x=2$的區間上的平均值定理的$x=c$。

5. 求滿足函式$f(x)=\sin(x)$以及區間$[0,\pi ]$上的平均值定理的點。

可導蘊含連續

如果$f'(x_{0})$存在，則$f$在$x_{0}$處連續。要看到這一點，請注意$\lim _{x\to x_{0}}(x-x_{0})f'(x_{0})=0$。但是

${\begin{aligned}\lim _{x\to x_{0}}(x-x_{0})f'(x_{0})&=\lim _{x\to x_{0}}(x-x_{0}){\frac {f(x)-f(x_{0})}{x-x_{0}}}\\&=\lim _{x\to x_{0}}(f(x)-f(x_{0}))\\&=\lim _{x\to x_{0}}f(x)-f(x_{0})\end{aligned}}$

這意味著$\lim _{x\to x_{0}}f(x)-f(x_{0})=0$ 或 $\lim _{x\to x_{0}}f(x)=f(x_{0})$，這表明$f$ 在 $x=x_{0}$ 處是連續的。

然而，反之則不成立。例如，取 $f(x)=|x|$。 $f$ 在 0 處是連續的，因為 $\lim _{x\to 0^{-}}|x|=\lim _{x\to 0^{-}}-x=0$ 且 $\lim _{x\to 0^{+}}|x|=\lim _{x\to 0^{+}}x=0$，且 $|0|=0$，但它在 0 處不可導，因為 $\lim _{h\to 0^{-}}{\frac {|0+h|-|0|}{h}}=\lim _{h\to 0^{-}}{\frac {-h}{h}}=-1$，但 $\lim _{h\to 0^{+}}{\frac {|0+h|-|0|}{h}}=\lim _{h\to 0^{+}}{\frac {h}{h}}=1$。