微積分/積分技巧/三角代換
三角代換背後的想法很簡單:用涉及標準三角函式的表示式替換涉及平方根的表示式,但不涉及平方根。涉及三角函式的積分通常比涉及平方根的積分更容易求解。
讓我們在實踐中演示這個想法。考慮表示式 。可能最基本的三角恆等式是 對於任意角度 。如果我們用 替換此表示式中的 ,藉助這個三角恆等式,我們看到
注意我們可以寫 因為我們用 替換了 。
需要指出的是,從技術角度而言,應該寫出 的絕對值,換句話說,就是 作為最終答案,因為對於所有可能的 都有 。但是,只要我們對所有可能的 的定義域以及 在最終計算中的使用方式保持謹慎,省略絕對值符號並不會構成問題。但是,我們不能直接將簡單的表示式 與複雜的 在任何地方互換,我們必須記住,在用換元法積分時,需要考慮導數。也就是說,我們需要記住 ,為了得到只包含 的積分,我們還需要用 來替換 。因此,如果我們看到一個形如
的積分,我們可以將其改寫為
請注意左側表示式中第一個 來自於替換 ,而 來自於用 替換。
由於 ,我們最初的積分簡化為
- .
最後這兩個積分很容易處理。對於第一個積分,我們得到
對於第二個積分,我們做一個替換,即 ,得到
最後我們看到
然而,這是以 為變數,而不是 ,所以我們必須代回去,才能用 重寫答案。
也就是說,我們算出了
因此我們得到了最終答案
正如你所見,即使對於一個看起來相當簡單的積分,這種方法也可能涉及到大量的計算。通常在使用三角代換之前,先看看是否可以用更簡單的方法來求解是很有幫助的。另一方面,在涉及平方根的被積函式中,這通常是最有效的方法。首先,我們將給出一些經驗規則來幫助你決定哪些三角代換可能會有所幫助。
如果被積函式包含以下形式的單個因子之一: 我們可以嘗試三角代換。
- 如果被積函式包含 ,令 ,並使用恆等式 。
- 如果被積函式包含 ,令 ,並使用恆等式 。
- 如果被積函式包含 ,令 ,並使用恆等式 。


正弦代換
[edit | edit source]
如果被積函式包含形式為 的部分,我們使用以下代換
這將把被積函式轉換為三角函式。如果新的被積函式無法直接積分,那麼下面描述的半形正切代換通常會將它轉換為一個更容易處理的代數被積函式。
例如,如果被積函式是,
如果被積函式是,我們可以將其改寫為
然後我們可以進行以下替換
正切替換
[edit | edit source]
當被積函式包含形式的部分時,我們使用以下替換
例如,如果被積函式是 ,那麼在進行這種代換後,我們發現
如果積分是
那麼在進行這種代換後,我們發現
經過分部積分和使用三角恆等式後,我們得到了一個包含原始積分的表示式。在這種情況下,我們現在必須重新排列方程,以便原始積分僅出現在一邊
正如我們從被積函式中預期的那樣,當 很大時,它近似於 。
在某些情況下,即使積分中沒有出現 ,也可以進行三角代換。
例如
該函式的分母等於 。這表明我們可以嘗試用 代換,並使用恆等式 。用這種代換,我們得到 ,因此
使用初始替換 得到
正割代換
[edit | edit source]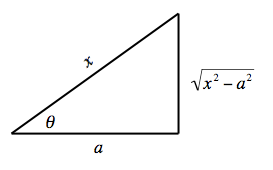
如果被積函式包含 形式的因子,我們使用以下替換
示例 1
[edit | edit source]求 。
求 .
現在我們可以用分部積分法
使用適當的三角代換求解以下積分。










































![{\displaystyle {\begin{aligned}\int \limits _{0}^{a}{\frac {1+x}{\sqrt {1-x^{2}}}}dx&=\int \limits _{0}^{\alpha }{\frac {1+\sin(\theta )}{\cos(\theta )}}\cos(\theta )d\theta &0<a<1\\&=\int \limits _{0}^{\alpha }{\bigl (}1+\sin(\theta ){\bigr )}d\theta &\alpha =\arcsin(a)\\&=\alpha +{\Big [}-\cos(\theta ){\Big ]}_{0}^{\alpha }\\&=\alpha +1-\cos(\alpha )\\&=1+\arcsin(a)-{\sqrt {1-a^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34bea926b8fc779d112222829c812acd2aa7561a)


![{\displaystyle {\begin{aligned}\int \limits _{0}^{z}(x^{2}+a^{2})^{-{\frac {3}{2}}}dx&=a^{-2}\int \limits _{0}^{\alpha }\cos(\theta )d\theta &z>0\\&=a^{-2}{\Big [}\sin(\theta ){\Big ]}_{0}^{\alpha }&\alpha =\arctan \left({\tfrac {z}{a}}\right)\\&=a^{-2}\sin(\alpha )\\&=a^{-2}{\frac {\frac {z}{a}}{\sqrt {1+{\frac {z^{2}}{a^{2}}}}}}\\&={\frac {z}{a^{2}{\sqrt {a^{2}+z^{2}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4664e0be89a175f0c7b393341bd8ad28bbeb24c)

![{\displaystyle {\begin{matrix}I&=&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &&&\alpha =\tan ^{-1}(z/a)\\&=&a^{2}\int _{0}^{\alpha }\sec \theta \,d\tan \theta &&&\\&=&a^{2}[\sec \theta \tan \theta ]_{0}^{\alpha }&-&a^{2}\int _{0}^{\alpha }\sec \theta \tan ^{2}\theta \,d\theta &\\&=&a^{2}\sec \alpha \tan \alpha &-&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\&=&a^{2}\sec \alpha \tan \alpha &-&I&+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313f2a452d4c096c9221cc6445317c894bb7eec0)


![{\displaystyle ={\tfrac {a^{2}}{2}}{\Bigg (}\sec(\alpha )\tan(\alpha )+{\bigg [}\ln {\Big (}\sec(\theta )+\tan(\theta ){\Big )}{\bigg ]}_{0}^{\alpha }{\Bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ca73ab74b8a68988b561b211957b826c9bcc9f)






















![{\displaystyle ={\bigg [}\tan(\theta )-\theta {\bigg ]}_{0}^{\alpha }\qquad \qquad \qquad \tan(\alpha )={\sqrt {\sec ^{2}(\alpha )-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf30ca894dfeaff2a765bb3ddb822a60753c656)





![{\displaystyle =-{\bigg [}\tan(\theta )\cos(\theta ){\bigg ]}_{0}^{\alpha }+\int \limits _{0}^{\alpha }\sec(\theta )d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abddc762382184a13946dc8522620aa0ad23dff4)
![{\displaystyle =-\sin(\alpha )+{\bigg [}\ln {\bigl (}\sec(\theta )+\tan(\theta ){\bigr )}{\bigg ]}_{0}^{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b45d861d862f65be50d6cf40c62770494cfa763)



