微積分/定積分

假設我們給定一個函式，想要確定其圖形在一個區間上的面積。我們可以猜想，但如何計算出確切的面積呢？下面，透過一些巧妙的思路，我們實際上 *定義* 這種面積，並表明透過使用所謂的 **定積分**，我們可以確切地確定曲線下的面積。

定積分的定義

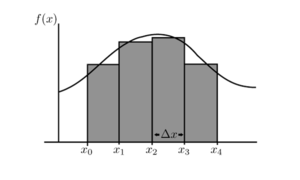圖 1: $f(x)$ 從 $x=x_{0}$ 到 $x=x_{4}$ 下的曲線面積的近似值。

圖 2: 從 $x_{2}$ 到 $x_{3}$ 下的曲線面積的近似矩形，取樣點為 $x_{3}^{*}$ 。

定義 $f$ 圖形下的面積的粗略思路是用有限個矩形來近似這個面積。由於我們可以很容易地計算出矩形的面積，因此我們得到了圖形下面積的估計。如果我們使用更多更小的矩形，我們預計圖形下曲線的面積會更精確，從而得到更好的近似值。在某種程度上，似乎我們可以使用我們從微分中熟悉的極限，並使用 “無限個” 矩形來得到確切的面積。讓我們更詳細地研究一下這樣的想法。

假設我們有一個在區間 $[a,b]$ 上為正的函式 $f$，我們想找到 $f$ 在 $a$ 和 $b$ 之間的面積 $S$。讓我們選擇一個整數 $n$，並將區間分成 $n$ 個寬度相等的子區間（參見圖 1）。由於區間 $[a,b]$ 的寬度為 $b-a$，每個子區間的寬度為 $\Delta x={\frac {b-a}{n}}$。我們用 $x_{0},x_{1},\ldots ,x_{n}$ 表示子區間的端點。這給了我們

$x_{i}=a+i\Delta x{\text{ for }}i=0,1,\dots ,n$

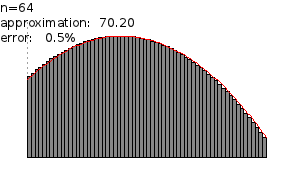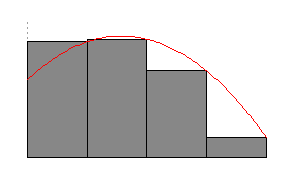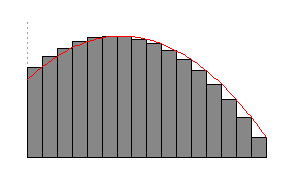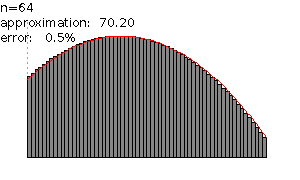圖 3：黎曼和隨著細分的增加，產生了更好的近似值。

現在，對於每個 $i=1,\ldots ,n$，選擇區間 $[x_{i-1},x_{i}]$ 內的一個 *取樣點* $x_{i}^{*}$，並考慮以 $f(x_{i}^{*})$ 為高，$\Delta x$ 為寬的矩形（參見 圖 2）。這個矩形的面積是 $f(x_{i}^{*})\Delta x$。透過將所有 $i=1,\ldots ,n$ 的矩形面積加起來，我們得到面積 $S$ 的近似值。

$A_{n}=f(x_{1}^{*})\Delta x+\dots +f(x_{n}^{*})\Delta x$

使用 求和符號 來表達會更加方便。

$A_{n}=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$

對於每個數 $n$，我們得到一個不同的近似值。當 $n$ 越來越大時，矩形的寬度越來越小，從而產生更好的近似值（參見 圖 3）。當 $A_{n}$ 隨著 $n$ 趨於無窮大時，我們得到面積 $S$。

定積分的定義
假設$f$ 是$[a,b]$ 上的連續函式，並且$\Delta x={\frac {b-a}{n}}$ 。那麼$f$ 在$a$ 和$b$ 之間的**定積分**是

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$

其中$x_{i}^{*}$ 是區間$[x_{i-1},x_{i}]$ 中的任意取樣點，並且$x_{k}=a+k\cdot \Delta x$ 對於$k=0,\dots ,n$ 。

事實上，如果$f$ 在$[a,b]$ 上是連續的，那麼這個極限總是存在的，並且不依賴於點$x_{i}^{*}\in [x_{i-1},x_{i}]$ 的選擇。例如，它們可以均勻分佈，也可以在區間內以任意方式分佈。這個證明是技術性的，超出了本節的範圍。

符號
在考慮表示式 $\int \limits _{a}^{b}f(x)dx$（讀作“從 $a$ 到 $b$ 的 $f$ 關於 $x$ 的積分 $dx$）時，函式 $f$ 被稱為被積函式，區間 $[a,b]$ 為積分割槽間。同時 $a$ 稱為積分下限，$b$ 稱為積分上限。

圖 4：積分表示圖形下的有符號面積。

這個定義的一個重要特徵是，我們也允許函式取負值。如果對於所有 $x$，有 $f(x)<0$，則 $f(x_{i}^{*})<0$，因此 $f(x_{i}^{*})\Delta x<0$。因此，$f$ 的定積分將是嚴格負數。更一般地，如果 $f$ 同時取正值和負值，那麼 $\int \limits _{a}^{b}f(x)dx$ 將是 $f$ 圖形正部分下的面積 **減去** 圖形負部分之上的面積（參見 圖 4）。因此，我們稱 $\int \limits _{a}^{b}f(x)dx$ 是圖形下的 **有符號面積**。

變數的獨立性

需要注意的是，變數 $x$ 在積分定義中並沒有扮演重要的角色。事實上，我們可以用任何其他字母來代替它，所以以下都是相等的

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{b}f(t)dt=\int \limits _{a}^{b}f(u)du=\int \limits _{a}^{b}f(w)dw$

每一個都是 $f$ 影像在 $a$ 和 $b$ 之間的有符號面積。這種變數通常被稱為 啞變數 或 約束變數。

左和右黎曼和

圖 5：右黎曼和

圖 6：左黎曼和

以下方法有時被稱為 L-RAM 和 R-RAM，RAM 代表“矩形逼近法”。

我們本可以決定選擇所有的樣本點 $x_{i}^{*}$ 在區間 $[x_{i-1},x_{i}]$ 的右側（見 圖 5）。然後 $x_{i}^{*}=x_{i}$ 對於所有的 $i$，我們稱之為 $A_{n}$ 的面積逼近就變成了

$A_{n}=\sum _{i=1}^{n}f(x_{i})\Delta x$

這被稱為 右黎曼和，而積分就是它的極限

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i})\Delta x$

或者，我們可以把每個樣本點都放在區間的左側。在這種情況下 $x_{i}^{*}=x_{i-1}$（見 圖 6），逼近就變成了

$A_{n}=\sum _{i=1}^{n}f(x_{i-1})\Delta x$

那麼 $f$ 的積分是

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i-1})\Delta x$

關鍵是，只要 $f$ 是連續的，這兩個定義得到的積分結果相同。

例子

例子 1
在這個例子中，我們將計算由 $f(x)=x$ 影像所確定的曲線在 $x$ 為 0 到 1 之間的曲線下的面積。首先，我們固定一個整數 $n$ ，並將區間 $[0,1]$ 分成 $n$ 個寬度相等的子區間。因此，每個子區間的寬度為

$\Delta x={\frac {1}{n}}$

為了計算積分，我們將使用右端黎曼和。（我們也可以使用左端和，最終結果相同）。對於右端和，樣本點為

$x_{i}^{*}=0+i\Delta x={\frac {i}{n}}\quad i=1,\ldots ,n$

請注意 $f(x_{i}^{*})=x_{i}^{*}={\frac {i}{n}}$ 。將此代入近似公式，得到

$A_{n}=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x=\sum _{i=1}^{n}f\left({\frac {i}{n}}\right)\Delta x=\sum _{i=1}^{n}{\frac {i}{n}}\cdot {\frac {1}{n}}={\frac {1}{n^{2}}}\sum _{i=1}^{n}i$

現在我們使用 公式

$\sum _{i=1}^{n}i={\frac {n(n+1)}{2}}$

得到

$A_{n}={\frac {1}{n^{2}}}\cdot {\frac {n(n+1)}{2}}={\frac {n+1}{2n}}$

為了計算$f$ 在$0$ 和$1$ 之間的積分，我們取$n$ 趨於無窮大的極限，

$\int \limits _{0}^{1}f(x)dx=\lim _{n\to \infty }{\frac {n+1}{2n}}={\frac {1}{2}}$

例2
接下來我們將展示如何找到函式$f(x)=x^{2}$ 在$x=a$ 和$x=b$ 之間的積分。這次區間$[a,b]$ 的寬度為$b-a$，所以

$\Delta x={\frac {b-a}{n}}$

我們再次使用右黎曼和。所以我們選擇的樣本點是

$x_{i}^{*}=a+i\Delta x=a+{\frac {i(b-a)}{n}}$

因此

$A_{n}$	$=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$
	$=\sum _{i=1}^{n}f\left(a+{\frac {(b-a)i}{n}}\right)\Delta x$
	$={\frac {b-a}{n}}\sum _{i=1}^{n}\left(a+{\frac {(b-a)i}{n}}\right)^{2}$
	$={\frac {b-a}{n}}\sum _{i=1}^{n}\left(a^{2}+{\frac {2a(b-a)i}{n}}+{\frac {(b-a)^{2}i^{2}}{n^{2}}}\right)$

我們需要計算這個等式右邊每一部分的值。對於前兩部分，

$\sum _{i=1}^{n}a^{2}=a^{2}\sum _{i=1}^{n}1=na^{2}$

$\sum _{i=1}^{n}{\frac {2a(b-a)i}{n}}={\frac {2a(b-a)}{n}}\sum _{i=1}^{n}i={\frac {2a(b-a)}{n}}\cdot {\frac {n(n+1)}{2}}$

對於第三個求和，我們需要使用一個公式

$\sum _{i=1}^{n}i^{2}={\frac {n(n+1)(2n+1)}{6}}$

得到

$\sum _{i=1}^{n}{\frac {(b-a)^{2}i^{2}}{n^{2}}}={\frac {(b-a)^{2}}{n^{2}}}{\frac {n(n+1)(2n+1)}{6}}$

將它們組合起來

$A_{n}={\frac {b-a}{n}}\left(na^{2}+{\frac {2a(b-a)}{n}}\cdot {\frac {n(n+1)}{2}}+{\frac {(b-a)^{2}}{n^{2}}}{\frac {n(n+1)(2n+1)}{6}}\right)$

當 $n$ 趨於無窮大時，極限為

$\int \limits _{a}^{b}x^{2}dx$	$=(b-a)\left(a^{2}+a(b-a)+{\frac {1}{3}}(b-a)^{2}\right)$
	$=(b-a)\left(a^{2}+ab-a^{2}+{\frac {1}{3}}(b^{2}-2ab+a^{2})\right)$
	$={\frac {1}{3}}(b-a)(b^{2}+ab+a^{2})$
	$={\frac {1}{3}}(b^{3}-a^{3})$

練習

1. 使用 5 個子區間上的左、右手黎曼和，求函式 $f(x)=x^{6}$ 從 $x=0$ 到 $x=1$ 區域的上下界。

2. 使用 5 個子區間上的左、右手黎曼和，求函式 $f(x)=x^{6}$ 從 $x=1$ 到 $x=2$ 區域的上下界。

積分的基本性質

從積分的定義中，我們可以推匯出一些基本性質。對於所有以下規則，假設 $f$ 和 $g$ 在 $[a,b]$ 上是連續的。

常數規則

常數規則 $\int \limits _{a}^{b}c\cdot f(x)dx=c\int \limits _{a}^{b}f(x)dx$

當 $f$ 為正數時，函式 $c\cdot f$ 在點 $x$ 處的函式高度是函式 $f$ 處的函式高度的 $c$ 倍。因此，$c\cdot f$ 在 $a$ 和 $b$ 之間的面積是 $f$ 之間面積的 $c$ 倍。我們也可以使用積分的定義，利用極限的常數規則來證明，

$\int \limits _{a}^{b}c\cdot f(x)dx=\lim _{n\to \infty }\sum _{i=1}^{n}c\cdot f(x_{i}^{*})=c\cdot \lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})=c\int \limits _{a}^{b}f(x)dx$

示例

我們在上一節中看到了

$\int \limits _{0}^{1}xdx={\frac {1}{2}}$

使用常數規則，我們可以用它來計算

$\int \limits _{0}^{1}3xdx=3\int \limits _{0}^{1}xdx=3\cdot {\frac {1}{2}}=1.5$ ,

$\int \limits _{0}^{1}-7xdx=-7\int \limits _{0}^{1}xdx=(-7)\cdot {\frac {1}{2}}=-3.5$ .

示例

我們在上一節中看到了

$\int \limits _{a}^{b}x^{2}dx={\frac {b^{3}-a^{3}}{3}}$

我們可以使用這個和常數規則來計算

$\int \limits _{1}^{3}2x^{2}dx=2\int \limits _{1}^{3}x^{2}dx=2\cdot {\frac {1}{3}}\cdot (3^{3}-1^{3})={\frac {2}{3}}(27-1)={\frac {52}{3}}$

該規則有一個用於積分常數的特殊情況。

積分常數
如果 $c$ 是常數，則 $\int \limits _{a}^{b}c\ dx=c(b-a)$

當 $c>0$ 且 $a<b$ 時，該積分是一個高度為 $c$，寬度為 $b-a$ 的矩形的面積，等於 $c(b-a)$。

示例

$\int \limits _{1}^{3}9dx=9(3-1)=9\cdot 2=18$

$\int \limits _{-2}^{6}11dx=11(6-(-2))=11\cdot 8=88$

$\int \limits _{2}^{17}0dx=0\cdot (17-2)=0$

加減法規則

積分的加減法規則
$\int \limits _{a}^{b}{\bigl (}f(x)+g(x){\bigr )}dx=\int \limits _{a}^{b}f(x)dx+\int \limits _{a}^{b}g(x)dx$

$\int \limits _{a}^{b}{\bigl (}f(x)-g(x){\bigr )}dx=\int \limits _{a}^{b}f(x)dx-\int \limits _{a}^{b}g(x)dx$

與常數規則一樣，加法規則遵循極限的加法規則。

$\int \limits _{a}^{b}{\bigl (}f(x)+g(x){\bigr )}dx$	$=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big (}f(x_{i}^{*})+g(x_{i}^{*}){\Big )}$
	$=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})+\lim _{n\to \infty }\sum _{i=1}^{n}g(x_{i}^{*})$
	$=\int \limits _{a}^{b}f(x)dx+\int \limits _{a}^{b}g(x)dx$

減法規則可以用類似的方法證明。

示例

從上面的例子中可以看出，$\int \limits _{1}^{3}9dx=18$ 以及 $\int \limits _{1}^{3}2x^{2}dx={\frac {52}{3}}$ 所以

$\int \limits _{1}^{3}(2x^{2}+9)dx=\int \limits _{1}^{3}2x^{2}dx+\int \limits _{1}^{3}9dx={\frac {52}{3}}+18={\frac {106}{3}}$

$\int \limits _{1}^{3}(2x^{2}-9)dx=\int \limits _{1}^{3}2x^{2}dx-\int \limits _{1}^{3}9dx={\frac {52}{3}}-18=-{\frac {2}{3}}$

示例

$\int \limits _{0}^{2}(4x^{2}+14)dx=4\int \limits _{0}^{2}x^{2}dx+\int \limits _{0}^{2}14dx=4\cdot {\frac {1}{3}}(2^{3}-0^{3})+2\cdot 14={\frac {32}{3}}+28={\frac {116}{3}}$

練習

3. 利用減法規則求出 $f(x)=x$ 和 $g(x)=x^{2}$ 在 $x=0$ 和 $x=1$ 之間的圖形面積。

比較規則

圖 7: 對 $f(x)$ 在 $[a,b]$ 上的面積進行邊界劃分

比較規則

• 假設對所有 $x\in [a,b]$，$f(x)\geq 0$。那麼

$\int \limits _{a}^{b}f(x)dx\geq 0$

• 假設對所有 $x\in [a,b]$，$f(x)\geq g(x)$。那麼

$\int \limits _{a}^{b}f(x)dx\geq \int \limits _{a}^{b}g(x)dx$

• 假設對所有 $x\in [a,b]$，$M\geq f(x)\geq m$。那麼

$M(b-a)\geq \int \limits _{a}^{b}f(x)dx\geq m(b-a)$

如果 $f(x)\geq 0$，則計算 $f$ 積分的黎曼和中的每個矩形都將在 $y$ 軸上方，因此面積將是非負的。如果 $f(x)\geq g(x)$，則 $f(x)-g(x)\geq 0$，根據第一個性質，我們得到第二個性質。最後，如果 $M\geq f(x)\geq m$，則 $f$ 影像下的面積將大於高度為 $m$ 的矩形的面積，小於高度為 $M$ 的矩形的面積（參見 圖 7）。所以

$M(b-a)=\int \limits _{a}^{b}M\geq \int \limits _{a}^{b}f(x)dx\geq \int \limits _{a}^{b}m=m(b-a)$

關於端點的線性

關於端點的可加性 假設 $a<c<b$。則

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx$

再次假設 $f$ 為正。那麼這個性質應該被理解為：$f$ 影像在 $a$ 和 $b$ 之間的面積等於 $a$ 和 $c$ 之間的面積加上 $c$ 和 $b$ 之間的面積（參見 圖 8）。

圖 8：關於端點的可加性性質的說明

關於積分限的可加性的擴充套件
當 $a=b$ 時，我們有 $\Delta x={\frac {b-a}{n}}=0$ 所以

$\int \limits _{a}^{a}f(x)dx=0$

此外，在定義積分時，我們假設了 $a<b$。但是，這個定義在 $b<a$ 時也有意義，在這種情況下， $\Delta x={\frac {b-a}{n}}$ 的符號發生了變化。這使得

$\int \limits _{b}^{a}f(x)dx=-\int \limits _{a}^{b}f(x)dx$

有了這些定義，

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx$

無論 $a,b,c$ 的順序如何。

練習

4. 使用練習 1 和 2 的結果以及關於端點的線性性質來確定 $\int \limits _{0}^{2}x^{6}dx$ 的上限和下限。

偶函式和奇函式

回想一下，如果函式 $f$ 滿足 $f(-x)=-f(x)$，則稱其為奇函式；如果滿足 $f(-x)=f(x)$，則稱其為偶函式。

假設 $f$ 是一個連續的奇函式，那麼對於任意 $a$，

$\int \limits _{-a}^{a}f(x)dx=0$

如果 $f$ 是一個連續的偶函式，那麼對於任意 $a$，

$\int \limits _{-a}^{a}f(x)dx=2\int \limits _{0}^{a}f(x)dx$

假設 $f$ 是一個奇函式，首先考慮從 $-a$ 到 $0$ 的積分。我們進行替換 $u=-x$，因此 $du=-dx$。請注意，如果 $x=-a$，那麼 $u=a$；如果 $x=0$，那麼 $u=0$。因此

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{a}^{0}f(-u)du=\int \limits _{0}^{a}f(-u)du$ .

由於 $f$ 是奇函式，$f(-u)=-f(u)$，因此積分變為

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{0}^{a}f(u)du$ .

現在我們可以用任何其他變數替換啞變數 $u$。因此，我們可以用字母 $x$ 替換它，得到

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{0}^{a}f(u)du=-\int \limits _{0}^{a}f(x)dx$ .

現在我們將積分分成兩部分

$\int \limits _{-a}^{a}f(x)dx=\int \limits _{-a}^{0}f(x)dx+\int \limits _{0}^{a}f(x)dx=-\int \limits _{0}^{a}f(x)dx+\int \limits _{0}^{a}f(x)dx=0$ .

偶函式公式的證明類似。

5. 證明如果 $f$ 是一個連續的偶函式，那麼對於任何 $a$，

$\int \limits _{-a}^{a}f(x)dx=2\int \limits _{0}^{a}f(x)dx$ .