微分是一個找到函式的過程,該函式輸出一個變數相對於另一個變數的變化率。
非正式地,我們可以假設我們正在跟蹤一輛汽車在一個沒有超車道的雙車道道路上的位置。假設汽車永遠不會駛離道路,我們可以抽象地研究汽車的位置,透過給它分配一個變數, 。由於汽車的位置隨著時間的推移而變化,我們說
。由於汽車的位置隨著時間的推移而變化,我們說 取決於時間,或者
取決於時間,或者 。這告訴我們汽車在每個特定時間的位置。微分給我們一個函式
。這告訴我們汽車在每個特定時間的位置。微分給我們一個函式 ,它表示汽車的速度,即其位置相對於時間的變化率。
,它表示汽車的速度,即其位置相對於時間的變化率。
等效地,微分給我們一個函式,它表示非線性函式圖在任何一點的斜率。對於線性函式,形式為 ,
, 是斜率。對於非線性函式,例如
是斜率。對於非線性函式,例如 ,斜率可能取決於
,斜率可能取決於 ;微分給我們一個函式,它表示這個斜率。
;微分給我們一個函式,它表示這個斜率。
歷史上,對微分的研究的主要動機是切線問題:對於給定的曲線,找到在給定點與曲線相切的直線的斜率。單詞tangent來自拉丁詞tangens,意思是接觸。因此,為了解決切線問題,我們需要找到與給定曲線在給定點“接觸”的直線的斜率,或者用現代語言來說,具有相同的斜率。但對於曲線來說,“斜率”到底是什麼意思呢?
在某些情況下,解決方案是顯而易見的:例如,直線 是它自己的切線;任何一點的斜率都是
是它自己的切線;任何一點的斜率都是 。對於拋物線
。對於拋物線 ,在點
,在點 的斜率是
的斜率是 ;切線是水平的。
;切線是水平的。
但如何找到,比如, 在
在  處的斜率? 這通常是一個非平凡的問題,但首先我們將仔細處理直線的斜率。
處的斜率? 這通常是一個非平凡的問題,但首先我們將仔細處理直線的斜率。
 三條斜率不同的直線
三條斜率不同的直線
直線的斜率,也稱為直線的梯度,是其傾斜程度的度量。水平的直線斜率為 0,從左下到右上的直線斜率為正,從左上到右下的直線斜率為負。
斜率可以用兩種(等效的)方式定義。第一種方式是將斜率表示為直線在水平方向上移動一定距離時上升的距離。我們使用符號  (讀作“delta”)來表示一個量的變化。因此,
(讀作“delta”)來表示一個量的變化。因此, 的變化寫成
的變化寫成  。因此,我們可以將這個斜率定義寫成
。因此,我們可以將這個斜率定義寫成

一個例子可以使這個定義更清晰。如果我們在一條直線上有兩個點, 和
和  ,從
,從  到
到  的
的  的變化由下式給出
的變化由下式給出

同樣,從  到
到  的
的  的變化由下式給出
的變化由下式給出

這導致了以下非常重要的結果。
或者,我們可以使用正切函式按三角函式的方式定義斜率

其中  是從指向右邊的水平線到直線的角度,以逆時針方向測量。如果你記得角度的正切是單位圓上 y 座標與 x 座標的比率,你應該能夠在這裡發現等價性。
是從指向右邊的水平線到直線的角度,以逆時針方向測量。如果你記得角度的正切是單位圓上 y 座標與 x 座標的比率,你應該能夠在這裡發現等價性。
我們感興趣的大多數函式的圖形都不是直線(儘管它們可以是),而是曲線。我們不能像定義直線斜率那樣定義曲線的斜率。為了理解如何在某一點上求曲線的斜率,我們首先需要了解 **切線** 的概念。直觀地說,**切線** 是一條在某一點 **恰好** 與曲線相切的直線,使得它們在該點的夾角為 0。考慮以下四條曲線和直線
- 直線
 穿過曲線
穿過曲線  在
在  點,但不是切線。
點,但不是切線。
- 直線
 穿過曲線
穿過曲線  在
在  點,並且是切線。
點,並且是切線。
- 直線
 穿過曲線
穿過曲線  在兩點,但只在
在兩點,但只在  點是切線。
點是切線。
- 有許多直線穿過曲線
 在
在  點,但沒有一條是切線。事實上,這條曲線在
點,但沒有一條是切線。事實上,這條曲線在  點沒有切線。
點沒有切線。
**割線** 是一條穿過曲線上兩點的直線。我們可以將切線定義為曲線割線在兩點間距離趨於零時的極限。考慮下圖。
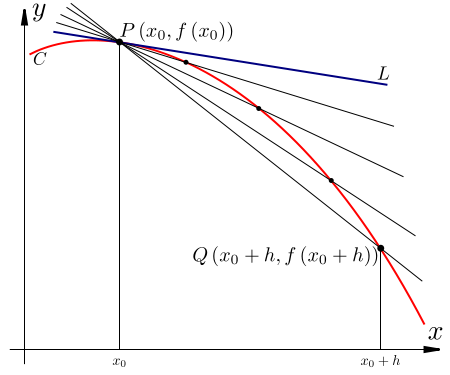
當距離  趨於 0 時,割線變為在
趨於 0 時,割線變為在  點的切線。我們繪製直線所經過的兩點是
點的切線。我們繪製直線所經過的兩點是

以及

割線只是一條直線,我們知道它上面的兩個點,所以我們可以找到它的斜率, ,使用之前公式。
,使用之前公式。

(我們將斜率稱為 ,因為它可能,而且通常會,取決於
,因為它可能,而且通常會,取決於 。)將直線上的點代入,
。)將直線上的點代入,

化簡得

這個表示式被稱為差商。注意 可以是正的或負的——穿過曲線上的任意兩點的割線都是完全有效的——但不能是
可以是正的或負的——穿過曲線上的任意兩點的割線都是完全有效的——但不能是 。
。
我們給出的切線定義並不嚴格,因為我們只定義了數字的極限——更確切地說,是輸出數字的函式的極限——而不是直線的極限。但我們可以嚴格地定義一個點處切線的斜率,方法是取上一段中割線的斜率的極限。這樣做了之後,我們就可以然後定義切線了。注意,我們不能簡單地將 設定為 0,因為這將意味著 0 除以 0,這將導致一個未定義的結果。相反,我們必須找到上面表示式的極限,當
設定為 0,因為這將意味著 0 除以 0,這將導致一個未定義的結果。相反,我們必須找到上面表示式的極限,當 趨於 0 時。
趨於 0 時。
最後一個等式只是經過 且斜率為
且斜率為  的直線的點斜式。
的直線的點斜式。
1. 求曲線

在點

處的切線的斜率。


解答
考慮  方向上的平均速度公式,
方向上的平均速度公式, ,其中
,其中 是時間間隔
是時間間隔  內
內  的變化量。這個公式給出了時間段內的平均速度,但假設我們想定義瞬時速度。為此,我們觀察了 **時間變化趨近於 0 時的位置變化**。用數學公式表示為:
的變化量。這個公式給出了時間段內的平均速度,但假設我們想定義瞬時速度。為此,我們觀察了 **時間變化趨近於 0 時的位置變化**。用數學公式表示為: ,我們用符號
,我們用符號  來簡寫。(這個符號的含義是字母
來簡寫。(這個符號的含義是字母  表示變化。)將符號
表示變化。)將符號  與
與  進行比較。兩者都表示兩個數字之間的差異,但
進行比較。兩者都表示兩個數字之間的差異,但  表示有限差異,而
表示有限差異,而  表示無窮小差異。請注意,符號
表示無窮小差異。請注意,符號  和
和  本身沒有嚴格的意義,因為
本身沒有嚴格的意義,因為  ,我們不能除以 0。
,我們不能除以 0。
(注意字母  通常用來表示距離,這將得出
通常用來表示距離,這將得出  。字母
。字母  通常在表示距離時避免使用,因為表示式
通常在表示距離時避免使用,因為表示式  會造成潛在的混淆。)
會造成潛在的混淆。)
你可能已經注意到,我們討論過的兩個操作——計算函式圖象切線的斜率和計算函式的瞬時變化率——涉及到完全相同的極限。也就是說, 圖象切線的斜率為
圖象切線的斜率為  。當然,
。當然, 可以,而且通常情況下,會取決於
可以,而且通常情況下,會取決於  ,所以我們應該把它看作是
,所以我們應該把它看作是  的一個函式。我們稱這個過程(計算
的一個函式。我們稱這個過程(計算  )為微分。微分得到另一個函式,該函式在任何值
)為微分。微分得到另一個函式,該函式在任何值  的值都是原函式在
的值都是原函式在  的斜率。這個函式被稱為原函式的導數。
的斜率。這個函式被稱為原函式的導數。
由於許多不同型別的人使用導數,所以存在許多不同的數學符號來表示它們。以下是一些例子:
 (讀作“f 對 x 的導數”)表示
(讀作“f 對 x 的導數”)表示  的導數,
的導數,![{\displaystyle D_{x}[f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0bc0c64c0455d3e24668b95c4790e57806572f3) ,
, ,
, 表示
表示  作為
作為  的函式的導數,或者
的函式的導數,或者![{\displaystyle {\frac {d}{dx}}{\big [}y{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a51a0607b2d4e9448055729d46246c4c9dc429) ,在某些情況下它更實用。
,在某些情況下它更實用。
大多數情況下,括號不是必需的,但如果我們要處理諸如 的情況,其中我們要對兩個函式
的情況,其中我們要對兩個函式 和
和  的乘積求導,則括號有助於提高畫質晰度。
的乘積求導,則括號有助於提高畫質晰度。
第一種表示法的優點是它明確表明導數是一個函式。也就是說,如果我們要談論 在
在 處的導數,我們可以簡單地寫成
處的導數,我們可以簡單地寫成 。
。
無論如何,以下是形式定義。
示例 1
 的導數為
的導數為

無論 是什麼。這與導數作為函式斜率的定義是一致的。
是什麼。這與導數作為函式斜率的定義是一致的。
示例 2
曲線  在
在  處的斜率是多少?我們可以透過“困難(且不精確)的方式”,即 *不* 使用微分來解決這個問題,如下所示,使用計算器和給定點上下的小差值。
處的斜率是多少?我們可以透過“困難(且不精確)的方式”,即 *不* 使用微分來解決這個問題,如下所示,使用計算器和給定點上下的小差值。
當  時,
時, 。
。
當  時,
時, 。
。
因此, 的兩個值的差為
的兩個值的差為  。
。
因此, 的兩個值的差為
的兩個值的差為  。
。
因此,曲線在  處的斜率為
處的斜率為  。
。
但是,為了精確地解決問題,我們計算

|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
我們這次很幸運;我們得到的近似值正好是正確的。但並不總是這樣,而且,無論如何,這樣我們就不需要計算器了。
通常, 的導數是
的導數是

|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
示例 3
如果  (絕對值函式),那麼
(絕對值函式),那麼  ,也可以寫成
,也可以寫成

求這個導數有點複雜,所以我們現在不證明它。
這裡, 在
在  處不光滑(雖然是連續的),因此極限
處不光滑(雖然是連續的),因此極限  和
和  (分別從右邊和左邊逼近 0 的極限)不等於。根據定義,
(分別從右邊和左邊逼近 0 的極限)不等於。根據定義, ,不存在。因此,
,不存在。因此, 未定義,因此
未定義,因此  在 0 處有一個間斷點。這種不可微分的點被稱為尖點。函式也可能因為在某一點處趨於無窮大或無限頻繁地振盪而不可微分。
在 0 處有一個間斷點。這種不可微分的點被稱為尖點。函式也可能因為在某一點處趨於無窮大或無限頻繁地振盪而不可微分。
導數符號在數學中是特殊且獨特的。初學微分時,最常見的導數符號是萊布尼茲符號,表示為  。你可以把它理解為“
。你可以把它理解為“ 相對於
相對於  的變化率”。你也可以把它理解為“
的變化率”。你也可以把它理解為“ 的無窮小值除以
的無窮小值除以  的無窮小值”。兩種理解方式都是很好的思考方式,但要記住,精確的定義是我們上面給出的那個。通常,在一個方程中,你會看到
的無窮小值”。兩種理解方式都是很好的思考方式,但要記住,精確的定義是我們上面給出的那個。通常,在一個方程中,你會看到  ,它的字面意思是“對 x 的導數”。這意味著我們應該對右邊寫的東西求導;也就是說,
,它的字面意思是“對 x 的導數”。這意味著我們應該對右邊寫的東西求導;也就是說, 意味著
意味著  ,其中
,其中  。
。
隨著你學習的深入,你會發現我們有時會假裝  和
和  是可以相乘和相除的獨立實體,透過寫類似於
是可以相乘和相除的獨立實體,透過寫類似於  的東西來表示。最終你會看到諸如
的東西來表示。最終你會看到諸如  這樣的導數,這僅僅意味著我們函式的輸入變數被稱為
這樣的導數,這僅僅意味著我們函式的輸入變數被稱為  ,而我們的輸出變數被稱為
,而我們的輸出變數被稱為  ;有時,我們會寫
;有時,我們會寫  ,表示對
,表示對  的導數,無論右邊寫了什麼。一般來說,變數可以是任何東西,比如
的導數,無論右邊寫了什麼。一般來說,變數可以是任何東西,比如  。
。
以下所有表示式都等效於表示  的導數
的導數





2. 使用導數定義求函式

的導數。


3. 使用導數定義求函式

的導數。現在試試

。你能看到規律嗎?在下一節中,我們將找到

對所有

的導數。


5. 在一張座標紙上繪製

的導數的圖形,無需求解

。然後,求解

並繪製其圖形;比較這兩個圖形。
6. 利用導數的定義證明

的導數是

。提示:使用合適的和差化積公式以及

和

。


解答
對於複雜的函式,微分過程非常繁瑣。因此,人們已經開發出了一些微分一般函式的規則,這些規則可以透過少量努力進行證明。一旦證明了足夠的規則,微分各種函式就會變得相對容易。一些最簡單的規則涉及線性函式的導數。
對於任何固定的實數  ,
,
![{\displaystyle {\frac {d}{dx}}[c]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/834381b512bc1d1fc47c2d26ce38ae71daaa1053)
函式  的影像是一條水平線,其斜率恆為 0。因此,可以預期該函式的導數為零,無論
的影像是一條水平線,其斜率恆為 0。因此,可以預期該函式的導數為零,無論  和
和  的值是多少。
的值是多少。
導數的定義是

設  對所有
對所有  成立。(也就是說,
成立。(也就是說, 是一個常數函式。)那麼
是一個常數函式。)那麼  。所以
。所以
![{\displaystyle {\frac {d}{dx}}[c]=\lim _{\Delta x\to 0}{\frac {c-c}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {0}{\Delta x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6429024c32c4dcbfab9e4f461bbf7c250e51f94)
設  。為了證明
。為了證明  ,我們需要找到一個正數
,我們需要找到一個正數  ,使得對於任何給定的正數
,使得對於任何給定的正數  ,只要
,只要  ,則
,則  。但是
。但是  ,所以
,所以  對於任何
對於任何  的選擇都成立。
的選擇都成立。
![{\displaystyle {\frac {d}{dx}}[3]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4971c461d4d1899584259a8cc861f594a720bfc6)
![{\displaystyle {\frac {d}{dx}}[z]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ee2f6002376e773eb77e8027a8b9969e6fa186)
請注意,在第二個例子中, 只是一個常數。
只是一個常數。
對於任何固定的實數  和
和  ,
,
![{\displaystyle {\frac {d}{dx}}[mx+c]=m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2233b08b6e33432899e0a6e4b5f10c04fa80180)
特殊情況  顯示了
顯示了  符號的優點 - 規則直觀,可以透過基本代數來理解,但這並不構成證明,並可能導致對
符號的優點 - 規則直觀,可以透過基本代數來理解,但這並不構成證明,並可能導致對  和
和  的本質是什麼的誤解。
的本質是什麼的誤解。
 的圖形是一條斜率為
的圖形是一條斜率為  的直線。
的直線。
如果  ,則
,則  。所以,
。所以,

|

|
|
|

|
|
|

|
|
|

|
|
|

|
由於我們已經知道一些非常基本函式的規則,我們希望能夠透過將更復雜的函式分解成更簡單的函式來求它們的導數。常數倍規則和加法規則是使我們能夠做到這一點的兩個工具。
對於任何固定的實數  ,
,
![{\displaystyle {\frac {d}{dx}}{\big [}c\cdot f(x){\big ]}=c\cdot {\frac {d}{dx}}{\big [}f(x){\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620f42e9b7e02ab5849561b877d00e9f3991cc9c)
原因當然是因為,人們可以在定義中將  從分子中因式分解出來,然後從整個極限中因式分解出來。細節留作 練習。
從分子中因式分解出來,然後從整個極限中因式分解出來。細節留作 練習。
示例
我們已經知道
![{\displaystyle {\frac {d}{dx}}{\big [}x^{2}{\big ]}=2x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f98d70aed6c89c1d7a7aa3afb8fa65cc1370d2)
假設我們要找到  的導數
的導數
![{\displaystyle {\frac {d}{dx}}{\big [}3x^{2}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bec61ad4893c0105e6ca724cc569f579acef837)
|
![{\displaystyle =3{\frac {d}{dx}}{\big [}x^{2}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/269595874a5ae15117c9b2ac88adc77f294b1f02)
|
|
|

|
|
|

|
另一個將函式分解的簡單規則是加法規則。
![{\displaystyle {\frac {d}{dx}}{\big [}f(x)\pm g(x){\big ]}={\frac {d}{dx}}{\big [}f(x){\big ]}\pm {\frac {d}{dx}}{\big [}g(x){\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aac5a3d2b8cb3ec27547f593f51f3623d6649f8)
證明
從定義
![{\displaystyle \lim _{\Delta x\to 0}\left[{\frac {{\big [}f(x+\Delta x)\pm g(x+\Delta x){\big ]}-{\big [}f(x)\pm g(x){\big ]}}{\Delta x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ed1e8360a288ade75ddcb507e376dd9cee55ec)
|
![{\displaystyle =\lim _{\Delta x\to 0}\left[{\frac {{\big [}f(x+\Delta x)-f(x){\big ]}\pm {\big [}g(x+\Delta x)-g(x){\big ]}}{\Delta x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ee0f6b5bb2a556f430421f7480eaea10469c133)
|
|
|
![{\displaystyle =\lim _{\Delta x\to 0}\left[{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\right]\pm \lim _{\Delta x\to 0}\left[{\frac {g(x+\Delta x)-g(x)}{\Delta x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/406f621d8790d9044a333148e0bb949e1af537ee)
|
根據定義,最後這一項是 ![{\displaystyle {\frac {d}{dx}}\left[f(x)\right]\pm {\frac {d}{dx}}\left[g(x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef506c07a97f260c7649fd622782c878eaaff692)
示例
請問  的導數是多少?
的導數是多少?
![{\displaystyle {\frac {d}{dx}}{\big [}3x^{2}+5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c9a04e8e8a83377a5f87ff165c4e0081b881ca)
|
![{\displaystyle ={\frac {d}{dx}}{\big [}3x^{2}+5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c95485942f79fba6dafa06b3994d360a65a3b747)
|
|
|
![{\displaystyle ={\frac {d}{dx}}{\big [}3x^{2}{\big ]}+{\frac {d}{dx}}{\big [}5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5fe7f0830a02ef2c17ba626724dc42b8f624708)
|
|
|
![{\displaystyle =6x+{\frac {d}{dx}}{\big [}5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40d69fd1b86b44bb1d43a9ec7fe819172ec0d523)
|
|
|

|
這兩個規則都起作用的事實,在數學上極其重要,因為它意味著微分是**線性的**。你可以將一個方程分解成多個項,分別求出導數,然後將答案重新組合,不會出現任何奇怪的事情。
現在,我們只需要再瞭解一點資訊,就可以求出任何多項式的導數了。
![{\displaystyle {\frac {d}{dx}}{\big [}x^{n}{\big ]}=nx^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ea2db0416ac0c9b3364fb54cc2e99d9342249df)
在指數函式和對數函式的導數中,有一個例子可以很好地說明這一點。
例如,在 的情況下,導數是
的情況下,導數是 ,如前所述。該規則的一個特例是
,如前所述。該規則的一個特例是 。
。
由於多項式是由單項式相加得到的,因此使用此規則和加法規則可以求出任何多項式的導數。從二項式定理可以推匯出一個相對簡單的證明。
此規則也適用於分數和負數冪。因此
![{\displaystyle {\frac {d}{dx}}{\big [}{\sqrt {x}}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7569884584a27c56af7a5333731d7a2d332e63ce)
|
![{\displaystyle ={\frac {d}{dx}}{\big [}x^{\frac {1}{2}}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7e66c17740cb48dc20d868a786193340fa4ba35)
|
|
|

|
|
|

|
掌握了這些規則後,你就可以求出任何多項式的導數了。我們不寫一般公式,而是逐步進行這個過程。
![{\displaystyle {\frac {d}{dx}}{\big [}6x^{5}+3x^{2}+3x+1{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68013f0aa462e583c6cab1228a3f2cd9f81c9645)
首先,我們可以使用加法規則將方程分解成多個項
![{\displaystyle {\frac {d}{dx}}{\big [}6x^{5}{\big ]}+{\frac {d}{dx}}{\big [}3x^{2}{\big ]}+{\frac {d}{dx}}{\big [}3x{\big ]}+{\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0adbd7509b1658e1b79408313dc3e439753abb10)
我們可以直接使用線性規則和常數規則來消除一些項
![{\displaystyle {\frac {d}{dx}}{\big [}6x^{5}{\big ]}+{\frac {d}{dx}}{\big [}3x^{2}{\big ]}+3+0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/399baa9d1f7a4b71032acd1e2731dab17809b790)
現在你可以使用常數乘法規則將常數移到導數之外
![{\displaystyle 6{\frac {d}{dx}}{\big [}x^{5}{\big ]}+3{\frac {d}{dx}}{\big [}x^{2}{\big ]}+3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ada9b3269f5fd71e399f6280c6881d85809f461a)
然後使用冪規則處理單個單項式

然後進行一些代數運算得到最終答案

這些不是唯一的微分規則。還有其他更高階的微分規則,將在後面的章節中介紹。
解答















































![{\displaystyle \lim _{h\to 0}\left[{\frac {f(x_{0}+h)-f(x_{0})}{h}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d4bd8965a03018d783a87573829f2113ec86fb4)
















![{\displaystyle D_{x}[f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0bc0c64c0455d3e24668b95c4790e57806572f3)

![{\displaystyle {\frac {d}{dx}}{\big [}y{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a51a0607b2d4e9448055729d46246c4c9dc429)




































































![{\displaystyle {\frac {d}{dx}}[c]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/834381b512bc1d1fc47c2d26ce38ae71daaa1053)



![{\displaystyle {\frac {d}{dx}}[c]=\lim _{\Delta x\to 0}{\frac {c-c}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {0}{\Delta x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6429024c32c4dcbfab9e4f461bbf7c250e51f94)







![{\displaystyle {\frac {d}{dx}}[3]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4971c461d4d1899584259a8cc861f594a720bfc6)
![{\displaystyle {\frac {d}{dx}}[z]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ee2f6002376e773eb77e8027a8b9969e6fa186)

![{\displaystyle {\frac {d}{dx}}[mx+c]=m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2233b08b6e33432899e0a6e4b5f10c04fa80180)








![{\displaystyle {\frac {d}{dx}}{\big [}c\cdot f(x){\big ]}=c\cdot {\frac {d}{dx}}{\big [}f(x){\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620f42e9b7e02ab5849561b877d00e9f3991cc9c)
![{\displaystyle {\frac {d}{dx}}{\big [}x^{2}{\big ]}=2x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f98d70aed6c89c1d7a7aa3afb8fa65cc1370d2)

![{\displaystyle {\frac {d}{dx}}{\big [}3x^{2}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bec61ad4893c0105e6ca724cc569f579acef837)
![{\displaystyle =3{\frac {d}{dx}}{\big [}x^{2}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/269595874a5ae15117c9b2ac88adc77f294b1f02)

![{\displaystyle {\frac {d}{dx}}{\big [}f(x)\pm g(x){\big ]}={\frac {d}{dx}}{\big [}f(x){\big ]}\pm {\frac {d}{dx}}{\big [}g(x){\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aac5a3d2b8cb3ec27547f593f51f3623d6649f8)
![{\displaystyle \lim _{\Delta x\to 0}\left[{\frac {{\big [}f(x+\Delta x)\pm g(x+\Delta x){\big ]}-{\big [}f(x)\pm g(x){\big ]}}{\Delta x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ed1e8360a288ade75ddcb507e376dd9cee55ec)
![{\displaystyle =\lim _{\Delta x\to 0}\left[{\frac {{\big [}f(x+\Delta x)-f(x){\big ]}\pm {\big [}g(x+\Delta x)-g(x){\big ]}}{\Delta x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ee0f6b5bb2a556f430421f7480eaea10469c133)
![{\displaystyle =\lim _{\Delta x\to 0}\left[{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\right]\pm \lim _{\Delta x\to 0}\left[{\frac {g(x+\Delta x)-g(x)}{\Delta x}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/406f621d8790d9044a333148e0bb949e1af537ee)
![{\displaystyle {\frac {d}{dx}}\left[f(x)\right]\pm {\frac {d}{dx}}\left[g(x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef506c07a97f260c7649fd622782c878eaaff692)

![{\displaystyle {\frac {d}{dx}}{\big [}3x^{2}+5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c9a04e8e8a83377a5f87ff165c4e0081b881ca)
![{\displaystyle ={\frac {d}{dx}}{\big [}3x^{2}+5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c95485942f79fba6dafa06b3994d360a65a3b747)
![{\displaystyle ={\frac {d}{dx}}{\big [}3x^{2}{\big ]}+{\frac {d}{dx}}{\big [}5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5fe7f0830a02ef2c17ba626724dc42b8f624708)
![{\displaystyle =6x+{\frac {d}{dx}}{\big [}5x{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40d69fd1b86b44bb1d43a9ec7fe819172ec0d523)

![{\displaystyle {\frac {d}{dx}}{\big [}x^{n}{\big ]}=nx^{n-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ea2db0416ac0c9b3364fb54cc2e99d9342249df)



![{\displaystyle {\frac {d}{dx}}{\big [}{\sqrt {x}}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7569884584a27c56af7a5333731d7a2d332e63ce)
![{\displaystyle ={\frac {d}{dx}}{\big [}x^{\frac {1}{2}}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7e66c17740cb48dc20d868a786193340fa4ba35)


![{\displaystyle {\frac {d}{dx}}{\big [}6x^{5}+3x^{2}+3x+1{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68013f0aa462e583c6cab1228a3f2cd9f81c9645)
![{\displaystyle {\frac {d}{dx}}{\big [}6x^{5}{\big ]}+{\frac {d}{dx}}{\big [}3x^{2}{\big ]}+{\frac {d}{dx}}{\big [}3x{\big ]}+{\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0adbd7509b1658e1b79408313dc3e439753abb10)
![{\displaystyle {\frac {d}{dx}}{\big [}6x^{5}{\big ]}+{\frac {d}{dx}}{\big [}3x^{2}{\big ]}+3+0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/399baa9d1f7a4b71032acd1e2731dab17809b790)
![{\displaystyle 6{\frac {d}{dx}}{\big [}x^{5}{\big ]}+3{\frac {d}{dx}}{\big [}x^{2}{\big ]}+3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ada9b3269f5fd71e399f6280c6881d85809f461a)







