微積分/空間中的曲線和曲面

← 向量	微積分	多元微積分 →
	空間中的曲線和曲面

對於許多實際應用，你必須使用直線、平面、曲線和曲面在三維空間中的數學描述。這需要一些關於向量的知識，以及在不使用計算器的情況下構建三維圖形的能力。

三維空間中的直線

雖然直線的方程在前面的章節中討論過（參見第7.1章），但本章將更詳細地解釋直線的性質和重要方面，以及擴充套件到三維空間中的一般曲線。

引數方程回顧

回想一下第5.1章，引數方程使用不同的變數來表達兩個變數之間的關係。例如，看看下面的圓的方程

$x^{2}+y^{2}=1$

如果我們將變數 $x$ 和 $y$ 用一個新的變數 $t$ 表示，並且我們知道 $\cos ^{2}t+\sin ^{2}t=1$ ，我們可以將原始方程改寫為

$x=\cos t$

$y=\sin t$

上面的方程是半徑為 $1$ 的圓的引數形式。

現在，讓我們談談三維空間中的直線。

三維空間中直線的方程

空間中的一條直線由空間中的兩個點定義，我將它們稱為 $P_{1}$ 和 $P_{2}$ 。令 $\mathbf {r} _{0}$ 為從原點到 $P_{1}$ 的向量， $\mathbf {r} _{2}$ 為從原點到 $P_{2}$ 的向量。給定這兩個點，直線上的其他任何點 $P$ 可以透過以下方式到達

\mathbf {r} =\mathbf {r} _{0}+\mathbf {v} t

其中 $\mathbf {v}$ 是從 $P_{1}$ 到 $P_{2}$ 的向量

\mathbf {v} =\mathbf {r} _{0}-\mathbf {r} _{2}

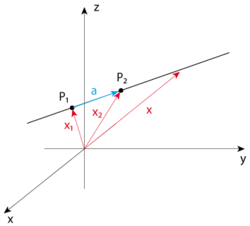
為了直觀地理解直線的方程，想象有一條直線經過向量 $\mathbf {r} _{0}$ 的端點，並沿向量 $\mathbf {v}$ 的方向延伸。只需將其視為點斜式的一個向量版本。例如，假設在三維空間中有一條直線，其方程為

$\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$

我們可以先找到點 $(2,5,4)$ ，然後將直線沿著向量 $\langle 1,1,1\rangle$ 平行方向拉伸。最終的圖形是直線 $\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 的圖形。有時方向向量 $\mathbf {v}$ 未知。但是，我們可以透過找到直線上的另一個點來輕鬆求解。在本例中，點 $(5,8,7)$ 在直線上。透過計算兩點之間的向量，我們可以發現方向向量是 $\langle 3,3,3\rangle$ 。因此，直線的方程可以寫成

$\mathbf {r} =\langle 2,5,4\rangle +\langle 3,3,3\rangle t_{1}$

它等價於原始方程 $\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ ，因為如果我們令 $t=3t_{1}$ ，原始方程將變為上面的方程。因此，使用向量形式來寫三維空間中直線的方程有無數種方法。現在，有一種引數形式可以表達直線。回想一下，還有另一種寫向量的方法： $a\mathbf {i} +b\mathbf {j} +c\mathbf {k}$ 。因此，我們可以將原始方程 $\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 重寫為

$\mathbf {r} =\langle 2+t,5+t,4+t\rangle =(2+t)\mathbf {i} +(5+t)\mathbf {j} +(4+t)\mathbf {k}$

然後，我們將各個部分分配給相應的 $x,y,z$ 軸

$x=2+t$
$y=5+t$
$z=4+t$

這是直線方程的引數形式。

最後，表示直線的常用方法是使用對稱方程，這只是引數形式的另一種微小變換。

$x-2=y-5=z-4$

概括地說，基本上有三種方法可以寫出透過點 $(x_{0},y_{0},z_{0})$ 且方向為 $\langle a,b,c\rangle$ 的直線方程。

向量方程	引數方程	對稱方程
$\mathbf {r} =\langle x_{0},y_{0},z_{0}\rangle +\langle a,b,c\rangle t$	$x=x_{0}+at$ $y=y_{0}+bt$ $z=z_{0}+ct$	${\frac {x-x_{0}}{a}}={\frac {y-y_{0}}{b}}={\frac {z-z_{0}}{c}}$

兩條直線之間的關係

有些直線彼此相交，有些則不相交。直線可以是平行、垂直或相交的，這些將在本部分討論。

交點

假設有兩條直線，它們的方程為

$L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 或引數形式 $L_{1}:{\begin{cases}x=2+t\\y=5+t\\z=4+t\end{cases}}$

$L_{2}:\langle 5,-1,0\rangle +\langle -{\frac {1}{2}},4,3\rangle s$ 或引數形式 $L_{2}:{\begin{cases}x=5-{\frac {1}{2}}s\\y=-1+4s\\z=3s\end{cases}}$

要找出它們是否相交，我們只需要解這個方程組

${\begin{cases}2+t=5-{\frac {1}{2}}s\\5+t=-1+4s\\4+t=3s\end{cases}}$

如果方程組只有一個解，那麼兩條直線在一點相交。如果方程組有無窮多解，那麼兩條直線重合。如果方程組沒有解，那麼兩條直線根本不相交。在本例中，有一個解

${\begin{cases}t=2\\s=2\end{cases}}$

因此，兩條直線在點 $(4,7,6)$ 相交。如果我們想進一步瞭解兩條直線之間的夾角，我們可以應用點積公式。兩條直線之間的夾角應該為

$\theta =\arccos({\frac {\mathbf {v_{1}} \,\cdot \,\mathbf {v_{2}} }{\|\mathbf {v_{1}} \|\|\mathbf {v_{2}} \|}})$

平行

要發現三維空間中的兩條平行直線，我們只需要檢視方向向量 $\mathbf {v}$ 。如果兩條直線 $\mathbf {v_{1}} ,\mathbf {v_{2}}$ 的方向向量滿足關係 $\mathbf {v_{2}} =k\mathbf {v_{1}} ,k\in \mathbb {R}$ ，那麼這兩條直線互相平行。例如，兩條直線 $L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 和 $L_{2}:\langle 5,-1,0\rangle +\langle -3,-3,-3\rangle s$ 互相平行，因為 ${\frac {\langle -3,-3,-3\rangle }{-3}}=\langle 1,1,1\rangle$ 。

垂直

要使兩條直線互相垂直，這兩條直線必須首先相交。如果它們確實相交，請回憶向量點積。點積指出

$\mathbf {a} \,\cdot \,\mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\cos \theta$

如果兩條直線互相垂直，則 $\theta ={\frac {\pi }{2}}$ ，由此得出 $\mathbf {a} \,\cdot \,\mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\cos {\frac {\pi }{2}}=0$ 。

因此，如果我們繼續這種思路，我們可以發現，如果我們在每條線上選擇兩個向量，對它們進行點積，結果為零，那麼我們可以安全地說這兩條線相互垂直。然而，有一個更方便的方法來簡化這個過程。我們不需要在每條線上找到兩個向量，而是隻需要對兩個方向向量應用點積，因為方向向量是從各自線上點計算出來的。

所以如果我們有兩條直線

$L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 和 $L_{2}:\langle 6,6,5\rangle +\langle -2,1,1\rangle s$

它們相互垂直，因為

${\begin{cases}2+t=6-2s\\5+t=6+s\\4+t=5+s\end{cases}}$ 只有一個解： ${\begin{cases}t=2\\s=1\end{cases}}$ ，這意味著它們相交。而且 $\langle 1,1,1\rangle \,\cdot \,\langle -2,1,1\rangle =0$

因此結束了證明。

異面直線

異面直線是不相交且不平行的直線。例如，直線 $L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 和 $L_{2}:\langle 5,-1,0\rangle +\langle 3,-3,-3\rangle s$ 是異面直線。

兩條異面直線之間的距離

要解決這個問題，我們需要了解三維空間中的平面，這將在下面討論。

三維空間中的平面

介紹

相同的思想可以用來描述三維空間中的平面，它由空間中三個點（不在一條線上）唯一確定（ $P_{1},P_{2},P_{3}$ ）。設 $\mathbf {x} _{i}$ 為從原點到 $P_{i}$ 的向量。那麼

\mathbf {x} =\mathbf {x} _{1}+\lambda \mathbf {a} +\mu \mathbf {b}

其中

\mathbf {a} =\mathbf {x} _{2}-\mathbf {x} _{1}\,\,{\text{and}}\,\,\mathbf {b} =\mathbf {x} _{3}-\mathbf {x} _{1}

注意，起點不一定要是 $\mathbf {x} _{1}$ ，可以是平面上的任何點。同樣，向量 $\mathbf {a}$ 和 $\mathbf {b}$ 唯一的條件是它們必須是我們平面上的兩個非共線向量。

回想一下，在二維向量中，如果有兩個向量 $\mathbf {i} ,\mathbf {j}$ ，笛卡爾平面上的任何向量都可以用向量 $\mathbf {i} ,\mathbf {j}$ 表示為 $a\mathbf {i} +b\mathbf {j} \quad (a,b\in \mathbb {R} )$ 。使用相同的方法，我們可以推斷出

the $\lambda \mathbf {a} +\mu \mathbf {b}$ 部分告訴我們圖形應該是平面，而 $\mathbf {x} -\mathbf {x} _{1}$ 部分描述了“斜率”和軸交點

但是，還有兩種方法可以表示三維空間中的平面：向量方程和標量方程。

平面的向量方程和標量方程

平面的向量方程要求我們理解點積的威力。我們已經知道，當兩個向量的點積為零時，這兩個向量應該相互垂直。現在，想象一個三維空間中的向量 $\mathbf {n}$ 。如果我們將所有與 $\mathbf {n}$ 垂直的向量 $\Delta \mathbf {r}$ 繪製出來，結果會是什麼？

結果應該是具有垂直於平面的向量的平面。因此，平面的向量方程只是 $\mathbf {n} \,\cdot \,\Delta \mathbf {r} =0$ 。

向量 $\mathbf {n}$ 是法向量，它垂直於平面

向量 $\Delta \mathbf {r} =\mathbf {r} -\mathbf {r_{0}}$ 是變數向量，其中 $\mathbf {r} =\langle x,y,z\rangle$ （平面上未知點）以及 $\mathbf {r_{0}} =\langle x_{0},y_{0},z_{0}\rangle$ （平面上給定點）。這個表示式僅僅意味著平面上所有向量。

當然，平面向量方程可以改寫為 $\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$ 或者 $\mathbf {n} \,\cdot \,\mathbf {r} =\mathbf {n} \,\cdot \,\mathbf {r_{0}}$ ，這取決於作者。

要找到標量方程，我們只需要計算點積並進行一些簡化。因此，假設

$\mathbf {n} =\langle a,b,c\rangle$ ， $\mathbf {r} =\langle x,y,z\rangle$ 以及 $\mathbf {r_{0}} =\langle x_{0},y_{0},z_{0}\rangle$ 根據向量方程
$\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$
因此，我們有
$\langle a,b,c\rangle \,\cdot \,\langle x-x_{0},y-y_{0},z-z_{0}\rangle =0$
經過一些代數運算，我們可以得到
$ax+by+cz-(ax_{0}+by_{0}+cz_{0})=0$
由於 $ax_{0}+by_{0}+cz_{0}$ 是一個常數，我們令 $ax_{0}+by_{0}+cz_{0}=-d$ 。因此，平面的標量方程為 $ax+by+cz+d=0$

注意常數 $a,b,c$ 與法向量的 $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ 分量相同。這個性質在討論兩個平面的關係時非常有用。此外， $-d=\mathbf {n} \,\cdot \,\mathbf {r_{0}}$ 。

$\blacksquare$

總結一下，有三種方法可以表示三維空間中的平面，後兩種更常用

從直線方程擴充套件	向量方程	標量方程
$\mathbf {x} =\mathbf {x} _{1}+\lambda \mathbf {a} +\mu \mathbf {b}$	$\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$	$ax+by+cz+d=0$

兩個平面的關係

平行

法向量很重要，因為它決定了平面的形狀。因此，當我們討論兩個平面的關係時，實際上是在嘗試找出兩個平面的法向量之間的聯絡。在本例中，假設三維空間中有兩個平面： $a_{1}x+b_{1}y+c_{1}z+d_{1}=0$ 和 $a_{2}x+b_{2}y+c_{2}z+d_{2}=0$ 。這兩個平面的法向量應該是

$\mathbf {n_{1}} =\langle a_{1},b_{1},c_{1}\rangle ,\,\mathbf {n_{2}} =\langle a_{2},b_{2},c_{2}\rangle$

由於法向量與其對應的平面垂直，如果法向量彼此平行，那麼它們對應的平面也應該彼此平行。因此，

如果 $\mathbf {n_{1}} =k\mathbf {n_{2}} \quad (k\in \mathbb {R} )$ ，那麼 $a_{1}x+b_{1}y+c_{1}z+d_{1}=0$ 和 $a_{2}x+b_{2}y+c_{2}z+d_{2}=0$ 彼此平行。

垂直

如果法向量互相垂直，則它們所在的平面也互相垂直。換句話說，如果 $\mathbf {n_{1}} \perp \mathbf {n_{2}}$ ，那麼這兩個平面互相垂直。

交點

為了完全理解如何找到兩條直線的交點，我們應該熟悉法向量及其潛在的應用。如果兩個平面不平行，並且不是同一個平面，那麼它們必須互相交叉。交點應該形成一條直線。想象一下，有兩個平面 $a_{1}x+b_{1}y+c_{1}z+d_{1}=0$ 和 $a_{2}x+b_{2}y+c_{2}z+d_{2}=0$ ，它們的各自的法向量 $\mathbf {n_{1}} \neq k\mathbf {n_{2}} \quad (k\in \mathbb {R} )$ （這意味著它們不平行）。

因為法向量與平面上所有向量完全垂直，所以反過來也成立：平面上所有向量都與它們各自的法向量垂直。這就是 $\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$ 是平面向量方程的原因。由於兩個平面的交點是一條直線，我們可以說方向向量 $\mathbf {v}$ 應該在這兩個平面上。

因為 $\mathbf {v}$ 位於兩個平面上， $\mathbf {v}$ 應該與兩個法向量垂直。
$\mathbf {v} \perp \mathbf {n_{1}} ,\,\mathbf {v} \perp \mathbf {n_{2}}$
回想一下，兩個向量的叉積將產生一個新的向量，該向量與這兩個原始向量都垂直。我們可以計算 $\mathbf {n_{1}} ,\mathbf {n_{2}}$ 的叉積來建立 $\mathbf {v}$ 。
$\mathbf {n_{1}} \times \mathbf {n_{2}} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\end{vmatrix}}=(b_{1}c_{2}-b_{2}c_{1})\mathbf {i} -(a_{1}c_{2}-a_{2}c_{1})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k}$
因此，這條線的方向向量為 $\mathbf {v} =\mathbf {n_{1}} \times \mathbf {n_{2}} =\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle$

我們還需要知道直線上的一點來完成方程式，因為 $\mathbf {r} =\mathbf {r} _{0}+\mathbf {v} t$ 。要找到一個點，只需設 $z=0$ ，然後在以下方程組中求解 $x,y$
${\begin{cases}a_{1}x+b_{1}y+d_{1}=0\\a_{2}x+b_{2}y+d_{2}=0\end{cases}}\Rightarrow {\begin{cases}x={\frac {b_{1}d_{2}-b_{2}d_{1}}{a_{1}b_{2}-a_{2}b_{1}}}\\y={\frac {a_{1}d_{2}-a_{2}d_{1}}{a_{2}b_{1}-a_{1}b_{2}}}\end{cases}}$
由於解過於複雜，無法寫下來，我們將讓 $x={\frac {b_{1}d_{2}-b_{2}d_{1}}{a_{1}b_{2}-a_{2}b_{1}}}=x_{0}$ 以及 $y={\frac {a_{1}d_{2}-a_{2}d_{1}}{a_{2}b_{1}-a_{1}b_{2}}}=y_{0}$ 。因此，點 $(x_{0},y_{0},0)$ 同時位於兩個平面（回想一下，我們令 $z=0$ ）上，並且 $\mathbf {P_{0}} =\langle x_{0},y_{0},0\rangle$ .

現在，我們知道直線 $(x_{0},y_{0},0)$ 上的一個點以及方向向量 $\mathbf {v} =\mathbf {n_{1}} \times \mathbf {n_{2}} =\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle$ ，這兩個平面的交線是： $L:\langle {\frac {b_{1}d_{2}-b_{2}d_{1}}{a_{1}b_{2}-a_{2}b_{1}}},{\frac {a_{1}d_{2}-a_{2}d_{1}}{a_{2}b_{1}-a_{1}b_{2}}},0\rangle +\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle t$

對於那些喜歡更簡潔表達的人

$L:\langle x_{0},y_{0},0\rangle +\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle t$

$L:\mathbf {P_{0}} +(\mathbf {n_{1}} \times \mathbf {n_{2}} )t$

如果要想知道兩個平面之間的夾角，類似於我們求兩條直線之間的夾角，可以應用點積

$\theta =\arccos({\frac {\mathbf {n_{1}} \,\cdot \,\mathbf {n_{2}} }{\|\mathbf {n_{1}} \|\|\mathbf {n_{2}} \|}})$

$\blacksquare$

兩個平行平面之間的距離

兩個不平行平面之間的距離為零，因為它們相交。所以，我們應該關注平行平面之間的距離。在我們進行之前，如果我們知道點到平面的距離，會更方便。

設距離為 $D$ ，點為 $P=(x_{1},y_{1},z_{1})$ ，平面為 $ax+by+cz+d=0$ .

知道平面的方程可以幫助我們知道法向量，因為法向量垂直於平面，是我們需要的準確方向。 $\mathbf {n} =\langle a,b,c\rangle$ .

現在，我們開始求解。首先，假設存在一個點 $P_{0}=(x_{0},y_{0},z_{0})$ 在平面 $ax+by+cz+d=0$ 上。然後，我們建立一個從 $P_{0}$ 到 $P$ 的向量： ${\overrightarrow {P_{0}P}}=\langle x_{1}-x_{0},y_{1}-y_{0},z_{1}-z_{0}\rangle$ 。我們還將向量 ${\overrightarrow {P_{0}P}}$ 和 $\mathbf {n}$ 之間的夾角設為 $\theta$ 。如果我們繪製出它的圖形，我們可以很容易地理解距離是如何推匯出來的。

$D=|\|{\overrightarrow {P_{0}P}}\|\ \cos \theta |$ （需要使用絕對值，因為距離應該始終大於零）

然而，我們不知道 $\theta$ 。我們可以透過應用點積來計算 $\theta$ 。但是，有一種更簡單的方法。

使用一些非常有趣的運算，我們可以得到
$D={\frac {|\|\mathbf {n} \|\|{\overrightarrow {P_{0}P}}\|\cos \theta |}{\|\mathbf {n} \|}}$
正如我們所見，分子實際上是表達兩個向量點積的另一種方式。因此，我們可以不再擔心不知道 $\theta$ 的值。
$D={\frac {|\mathbf {n} \ \cdot \ {\overrightarrow {P_{0}P}}|}{\|\mathbf {n} \|}}$
我們現在可以用它們的座標來替換這些向量。經過一些代數運算，我們得到
$D={\frac {|\mathbf {n} \ \cdot \ {\overrightarrow {P_{0}P}}|}{\|\mathbf {n} \|}}={\frac {|ax_{1}+by_{1}+cz_{1}-(ax_{0}+by_{0}+cz_{0})|}{\sqrt {a^{2}+b^{2}+c^{2}}}}$
由於 $P_{0}=(x_{0},y_{0},z_{0})$ 在平面上， $ax_{0}+by_{0}+cz_{0}=-d$ 。我們可以進一步簡化公式為 $D={\frac {|ax_{1}+by_{1}+cz_{1}+d|}{\sqrt {a^{2}+b^{2}+c^{2}}}}$ ，從而完成了我們的推導。

還有其他方法可以寫出該公式。對於喜歡更簡單符號的人來說，以下公式也是表示距離的方法

$D={\frac {|\mathbf {n} \ \cdot \ {\overrightarrow {P_{0}P}}|}{\|\mathbf {n} \|}}$ 或 $D=\mathrm {comp} _{\mathbf {n} }{\overrightarrow {P_{0}P}}$

$\blacksquare$

經過對距離公式的進一步“研究”，我們可以發現，只需要平面的方程和一個點就可以計算它們之間的距離，這非常方便，因為我們需要解決問題的因素越少，問題就越方便。當我們嘗試找到兩個平行平面之間的距離時，我們只需要一個平面上的一個點和平面的方程來解決。

兩條異面直線之間的距離（續）

假設直線 $L_{1},L_{2}$ 是異面直線，我們可以透過假設這些直線屬於兩個平行平面 $P_{1},P_{2}$ 來計算距離。然後，問題就從求解兩條異面直線之間的距離變為求解兩個平行平面之間的距離。

我們仍然需要知道兩個平面的法向量。我們可以簡單地對兩條直線的兩個方向向量進行叉積運算： $\mathbf {n} =\mathbf {v_{1}} \times \mathbf {v_{2}}$ 。 $\mathbf {n} \neq 0$ 因為 $\mathbf {v_{1}} ,\mathbf {v_{2}}$ 並不指向相同的方向。現在我們可以將新推匯出的距離公式應用於兩條異面直線。

圓柱體和二次曲面

本章節需要您對圓錐曲線有一定的瞭解（參見第1.6章）。

圓柱

圓柱面是由所有平行於一條給定直線並穿過給定平面曲線的直線組成的曲面。存在幾種特殊的圓柱面，例如拋物柱面和圓柱面。例如，右側的影像是拋物柱面。拋物柱面通常具有以下方程

$z=x^{2}$ 等。

如果我們想在不旋轉的情況下移動圓柱體，我們可以有以下方程

$z-k=(x-h)^{2}$ ，其中 $h,k$ 是常數。

這與我們在第1.6章早期討論過的拋物線類似，但增加了一個新的維度。圓柱面，類似於我們推匯出拋物柱面的方式，看起來就像一個圓柱體，其“底面”是圓形，方程為

$x^{2}+y^{2}=1$ 等。

如果我們想使圓柱面更“橢圓形”，就像我們推匯出橢圓方程的方式一樣，橢圓柱面具有以下方程

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ ，其中 $a,b$ 是常數。

這就像 $xy$ 平面上的一個橢圓，但在 $z$ 方向上無限延伸。

二次曲面

二次曲面的通用方程

二次曲面的通用方程為

Ax^{2}+By^{2}+Cz^{2}+Dxy+Eyz+Fxz+Gx+Hy+Iz+J=0

其中 $A,B,C,D,E,F,G,H,I,J$ 是常數。

它看起來類似於圓錐曲線的通用方程（ $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ ），除了它還有一個變數 $z$ 。經過一些平移和旋轉，我們可以將通用方程簡化為標準方程

二次曲面的標準方程

二次曲面的標準方程為

Ax^{2}+By^{2}+Cz^{2}+J=0\quad {\text{or}}\quad Ax^{2}+By^{2}+Iz=0

其中 $A,B,C,I,J$ 是常數。

當然，根據具體的二次曲面，存在不同的標準方程形式，我們將在接下來的討論中看到。

橢球面

橢球的方程為

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1$

繪製二次曲面比較困難，因為不像二維平面那樣只有兩個變數，而是有三個變數，如果沒有計算器的幫助，繪製過程會非常複雜。但是，有一種方法可以讓我們更容易理解。我們可以分析每個平面上的形狀，然後將每個平面上的分析結果組合起來，形成一個相當完整的曲面圖。以這個為例

$x^{2}+{\frac {y^{2}}{9}}+{\frac {z^{2}}{4}}=1$

首先讓我們檢查 $xy$ -平面。為了檢查 $xy$ -平面，我們需要想象 $z$ 為一個常數。在這種情況下，假設 $z=k$ ，那麼

$x^{2}+{\frac {y^{2}}{9}}=1-{\frac {k^{2}}{4}}$ ，其中 $-2\leq k\leq 2$ 。

我們可以看到，在 $xy$ -平面上，圖形將像一個橢圓。我們稱之為在平面 $z=k$ 上的水平截面為橢圓。

讓我們進一步分析在平面 $x=k,y=k$ 上的垂直截面。

${\frac {y^{2}}{9}}+{\frac {z^{2}}{4}}=1-k^{2}\quad x=k$ ，其中 $-1\leq k\leq 1$ 。

$x^{2}+{\frac {z^{2}}{4}}=1-{\frac {k^{2}}{9}}\quad y=k$ ，其中 $-3\leq k\leq 3$ 。

我們可以看到，在平面 $x=k,y=k$ 上的兩個垂直截面上都是橢圓。換句話說，在 $xz$ 平面和 $yz$ 平面上，圖形看起來像橢圓。由於所有截面都是橢圓，所以該曲面是一個橢球，頂點為 $(\pm 1,0,0),(0,\pm 3,0),(0,0,\pm 2)$ 。

橢圓拋物面

橢圓拋物面的方程為

${\frac {z}{c}}={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}$

根據哪個截面是橢圓，方程會有所不同。對於上面的方程，水平截面是橢圓，如右圖所示。

例如，取 $z=x^{2}+y^{2}$ ，水平截面，即 $z=k$ 為

$x^{2}+y^{2}=k$ ，其中 $k>0$ 。

對於兩個垂直截面，我們可以看到它們都是拋物線形狀。

$z=x^{2}+k^{2}\quad y=k$

$z=y^{2}+k^{2}\quad x=k$

該橢圓拋物面的頂點為 $(0,0,0)$ 。

雙曲拋物面

雙曲拋物面的方程為

${\frac {z}{c}}={\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}$

相應的截面是

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}={\frac {k}{c}}\quad z=k$ ，其中 ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}={\frac {k}{c}}{\text{ when }}k>0\quad {\text{and}}\quad {\frac {y^{2}}{b^{2}}}-{\frac {x^{2}}{a^{2}}}={\frac {k}{c}}{\text{ when }}k<0$ 。水平截面是雙曲線。

${\frac {z}{c}}={\frac {x^{2}}{a^{2}}}-{\frac {k^{2}}{b^{2}}}\quad y=k$ 。垂直截面是拋物線。

${\frac {z}{c}}={\frac {k^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}\quad x=k$ 。垂直截面是拋物線。