在大多數數學課程中,到目前為止,我們處理的是**標量**。這些是隻需要一個數字來表示的量。例如,駕駛去雜貨店的汽油量是一個標量,因為它只需要一個數字:2 加侖。
在本單元中,我們處理的是**向量**。向量是一個**有向線段** - 也就是說,一個指向一個方向或另一個方向的線段。因此,它有一個**起點**和一個**終點**。向量從起點開始,到終點結束,並且向量指向終點。向量繪製為一個帶有終點箭頭的線段
單個沒有座標軸的向量。 4 2 {\displaystyle 4{\sqrt {2}}}
同一個向量的多個位置。 然而,習慣上將向量放置在起點位於原點的座標系中,如黑色向量所示。這稱為**標準位置**。
在標準做法中,我們不透過列出長度和方向來表達向量。相反,我們使用**分量形式**,它列出向量的垂直高度(上升)和水平寬度(執行)。寫成如下形式
( run rise ) {\displaystyle {\begin{pmatrix}{\text{run}}\\{\text{rise}}\end{pmatrix}}}
表示分量形式的向量還有其他方法,包括
( u x , u y ) {\displaystyle \mathbf {(u_{x},u_{y})} } 和
⟨ u x , u y ⟩ {\displaystyle \mathbf {\left\langle u_{x},u_{y}\right\rangle } } 從圖中我們可以看到標準位置的優點:終點的座標的兩個數字與向量的上升和下降的兩個數字相同。注意我們把這個向量命名為 u {\displaystyle \mathbf {u} } x , y , z {\displaystyle x,y,z} u , v , w {\displaystyle u,v,w}
當以分量形式表示向量時,不再明顯地知道其大小和方向。因此,我們必須進行一些計算才能找到大小和方向。
| u | = u x 2 + u y 2 {\displaystyle |\mathbf {u} |={\sqrt {u_{x}^{2}+u_{y}^{2}}}} 其中 u x {\displaystyle u_{x}} u y {\displaystyle u_{y}}
向量的長度也可以稱為範數。
tan ( θ ) = u y u x {\displaystyle \tan(\theta )={\frac {u_{y}}{u_{x}}}}
其中 θ {\displaystyle \theta } x {\displaystyle x}
對於這些定義,假設
u = ( u x u y ) , v = ( v x v y ) {\displaystyle \mathbf {u} ={\begin{pmatrix}u_{x}\\u_{y}\end{pmatrix}},\mathbf {v} ={\begin{pmatrix}v_{x}\\v_{y}\end{pmatrix}}} 向量加法通常被稱為首尾相連 加法,因為這更容易記住。
你正在加的向量的總和被稱為合向量,它是從第一個向量的起點(首)到第二個向量的終點(尾)所畫的向量。儘管它們看起來像箭頭,但尖頭部分是尾部,而不是首部。(想象一下你在沿著向量指向的方向行走...... 你會從平的一端(首)開始,朝著尖的一端走去。)
它看起來像這樣
(注意,黑線向量是兩個點線向量的總和!)
( 4 6 ) + ( 1 − 3 ) = ( 5 3 ) {\displaystyle {\binom {4}{6}}+{\binom {1}{-3}}={\binom {5}{3}}}
或者更一般地
u + v = ( u x + v x u y + v y ) {\displaystyle \mathbf {u} +\mathbf {v} ={\begin{pmatrix}u_{x}+v_{x}\\u_{y}+v_{y}\end{pmatrix}}}
從圖形上看,用標量乘以一個向量只改變向量的長度,並且是乘以同一個標量。也就是說,用 2 乘以一個向量將會把向量“拉伸”到其原始長度的兩倍,而方向保持不變。
2 ⋅ ( 3 3 ) = ( 6 6 ) {\displaystyle 2\cdot {\binom {3}{3}}={\binom {6}{6}}} 在數值上,可以用以下公式計算出結果向量
c u = ( c u x c u y ) {\displaystyle c\mathbf {u} ={\begin{pmatrix}cu_{x}\\cu_{y}\end{pmatrix}}} ,其中
c {\displaystyle c} 是一個常數標量。
如前所述,長度會乘以相同的常數
| c u | = | c | | u | {\displaystyle |c\mathbf {u} |=|c||\mathbf {u} |} 由於用一個常數乘以一個向量會得到一個方向相同的向量,所以我們可以推斷,如果一個向量是另一個向量的常數倍,那麼這兩個向量是平行的——也就是說, u | | v {\displaystyle \mathbf {u} ||\mathbf {v} } u = c v {\displaystyle \mathbf {u} =c\mathbf {v} } c {\displaystyle c}
我們也可以用倒數乘以一個非零標量來除以它,就像除以普通數字一樣
u c = 1 c u , c ≠ 0 {\displaystyle {\frac {\mathbf {u} }{c}}={\frac {1}{c}}\mathbf {u} ,c\neq 0} 對應用於二維向量的函式,線性性質的描述。在本圖中,很明顯 L ( u + v ) = L ( u ) + L ( v ) {\displaystyle L(\mathbf {u} +\mathbf {v} )=L(\mathbf {u} )+L(\mathbf {v} )} 給定一個函式 L {\displaystyle L} L {\displaystyle L}
對於任何向量 u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} } L ( u + v ) = L ( u ) + L ( v ) {\displaystyle L(\mathbf {u} +\mathbf {v} )=L(\mathbf {u} )+L(\mathbf {v} )}
對於任何向量 u {\displaystyle \mathbf {u} } c {\displaystyle c} L ( c u ) = c L ( u ) {\displaystyle L(c\mathbf {u} )=cL(\mathbf {u} )} 更一般地,當給定一個具有多個向量值引數的函式 M {\displaystyle M} u 1 , u 2 , . . . , u n {\displaystyle \mathbf {u} _{1},\mathbf {u} _{2},...,\mathbf {u} _{n}} M {\displaystyle M} M {\displaystyle M}
對於每個 i = 1 , 2 , . . . , n {\displaystyle i=1,2,...,n} u 1 , u 2 , … , u n {\displaystyle \mathbf {u} _{1},\mathbf {u} _{2},\dots ,\mathbf {u} _{n}}
對於與 u i {\displaystyle \mathbf {u} _{i}} v {\displaystyle \mathbf {v} } M ( u 1 , . . . , u i + v , . . . , u n ) = M ( u 1 , . . . , u i , . . . , u n ) + M ( u 1 , . . . , v , . . . , u n ) {\displaystyle M(\mathbf {u} _{1},...,\mathbf {u} _{i}+\mathbf {v} ,...,\mathbf {u} _{n})=M(\mathbf {u} _{1},...,\mathbf {u} _{i},...,\mathbf {u} _{n})+M(\mathbf {u} _{1},...,\mathbf {v} ,...,\mathbf {u} _{n})}
對於任何標量 c {\displaystyle c} M ( u 1 , . . . , c u i , . . . , u n ) = c M ( u 1 , . . . , u i , . . . , u n ) {\displaystyle M(\mathbf {u} _{1},...,c\mathbf {u} _{i},...,\mathbf {u} _{n})=cM(\mathbf {u} _{1},...,\mathbf {u} _{i},...,\mathbf {u} _{n})} 如果 n = 2 {\displaystyle n=2} M {\displaystyle M}
點積是一種將兩個向量相乘以產生一個標量值的方法。因為它將兩個向量的分量組合起來形成一個/標量/,所以它有時被稱為標量積。如果你被要求對兩個矩形向量進行“點積”,你會做以下操作
u ⋅ v = u x v x + u y v y {\displaystyle \mathbf {u} \cdot \mathbf {v} =u_{x}v_{x}+u_{y}v_{y}} 需要特別注意的是,兩個向量的點積不會 產生另一個向量,它會給你一個標量,只是一個數值。
如果你的向量不是矩形(“笛卡爾”)格式,可能會出現另一個常見的陷阱。有時,向量以極座標表示,其中第一個分量是向量的幅度(長度),第二個分量是相對於 x {\displaystyle x}
透過一些重排和三角函式操作,我們可以看到,兩個向量點積得到的結果是一個令人驚訝且有用的恆等式
u ⋅ v = | u | | v | cos ( θ ) {\displaystyle \mathbf {u} \cdot \mathbf {v} =|\mathbf {u} ||\mathbf {v} |\cos(\theta )} 其中 θ {\displaystyle \theta }
使用點積計算像甲烷這樣的對稱四面體分子的鍵角 這提供了一種方便的方法來找到兩個向量之間的夾角
cos ( θ ) = u ⋅ v | u | | v | {\displaystyle \cos(\theta )={\frac {\mathbf {u} \cdot \mathbf {v} }{|\mathbf {u} ||\mathbf {v} |}}}
注意,點積是“可交換的”,也就是說
u ⋅ v = v ⋅ u {\displaystyle \mathbf {u} \cdot \mathbf {v} =\mathbf {v} \cdot \mathbf {u} } 此外,兩個向量的點積將是向量長度的平方
u ⋅ u = u x u x + u y u y = ( u x ) 2 + ( u y ) 2 {\displaystyle \mathbf {u} \cdot \mathbf {u} =u_{x}u_{x}+u_{y}u_{y}=(u_{x})^{2}+(u_{y})^{2}} 根據勾股定理,
( u x ) 2 + ( u y ) 2 = | u | 2 {\displaystyle (u_{x})^{2}+(u_{y})^{2}=|\mathbf {u} |^{2}} 點積可以被視為一個向量投影到另一個向量上的長度。換句話說,點積詢問“這個向量的多少大小指向那個向量方向?”
從點積的以下定義開始: u ⋅ v = | u | | v | cos ( θ ) {\displaystyle \mathbf {u} \cdot \mathbf {v} =|\mathbf {u} ||\mathbf {v} |\cos(\theta )} θ {\displaystyle \theta } u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} }
公式 u ⋅ v = u x v x + u y v y {\displaystyle \mathbf {u} \cdot \mathbf {v} =u_{x}v_{x}+u_{y}v_{y}}
三角形 Δ A O B {\displaystyle \Delta AOB} 方法 1
一種較為直接的方法是利用餘弦定理。建立一個三角形 Δ A O B {\displaystyle \Delta AOB} A ( u x , u y ) {\displaystyle A(u_{x},u_{y})} O ( 0 , 0 ) {\displaystyle O(0,0)} B ( v x , v y ) {\displaystyle B(v_{x},v_{y})} O A → = u {\displaystyle {\vec {OA}}=\mathbf {u} } O B → = v {\displaystyle {\vec {OB}}=\mathbf {v} } A B → = v − u {\displaystyle {\vec {AB}}=\mathbf {v} -\mathbf {u} } ∠ A O B = θ {\displaystyle \angle AOB=\theta }
三角形的邊長分別為 | O A | = | u | {\displaystyle |OA|=|\mathbf {u} |} | O B | = | v | {\displaystyle |OB|=|\mathbf {v} |} | A B | = | v − u | {\displaystyle |AB|=|\mathbf {v} -\mathbf {u} |}
| A B | 2 = | O A | 2 + | O B | 2 − 2 | O A | | O B | cos ( ∠ A O B ) {\displaystyle |AB|^{2}=|OA|^{2}+|OB|^{2}-2|OA||OB|\cos(\angle AOB)} ⟺ | v − u | 2 = | u | 2 + | v | 2 − 2 | u | | v | cos ( θ ) {\displaystyle \iff |\mathbf {v} -\mathbf {u} |^{2}=|\mathbf {u} |^{2}+|\mathbf {v} |^{2}-2|\mathbf {u} ||\mathbf {v} |\cos(\theta )} ⟺ ( v x − u x ) 2 + ( v y − u y ) 2 = ( u x 2 + u y 2 ) + ( v x 2 + v y 2 ) − 2 | u | | v | cos ( θ ) {\displaystyle \iff (v_{x}-u_{x})^{2}+(v_{y}-u_{y})^{2}=(u_{x}^{2}+u_{y}^{2})+(v_{x}^{2}+v_{y}^{2})-2|\mathbf {u} ||\mathbf {v} |\cos(\theta )} ⟺ − 2 u x v x − 2 u y v y = − 2 | u | | v | cos ( θ ) {\displaystyle \iff -2u_{x}v_{x}-2u_{y}v_{y}=-2|\mathbf {u} ||\mathbf {v} |\cos(\theta )} ⟺ | u | | v | cos ( θ ) = u x v x + u y v y {\displaystyle \iff |\mathbf {u} ||\mathbf {v} |\cos(\theta )=u_{x}v_{x}+u_{y}v_{y}}
因此 u ⋅ v = u x v x + u y v y {\displaystyle \mathbf {u} \cdot \mathbf {v} =u_{x}v_{x}+u_{y}v_{y}}
方法 2
對 u ⋅ v = u x v x + u y v y {\displaystyle \mathbf {u} \cdot \mathbf {v} =u_{x}v_{x}+u_{y}v_{y}}
保持 u {\displaystyle \mathbf {u} } u ⋅ v {\displaystyle \mathbf {u} \cdot \mathbf {v} } v {\displaystyle \mathbf {v} }
保持 v {\displaystyle \mathbf {v} } u ⋅ v {\displaystyle \mathbf {u} \cdot \mathbf {v} } u {\displaystyle \mathbf {u} } 由於從定義 u ⋅ v = | u | | v | cos ( θ ) {\displaystyle \mathbf {u} \cdot \mathbf {v} =|\mathbf {u} ||\mathbf {v} |\cos(\theta )} u ⋅ v = v ⋅ u {\displaystyle \mathbf {u} \cdot \mathbf {v} =\mathbf {v} \cdot \mathbf {u} } v {\displaystyle \mathbf {v} } u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} }
v {\displaystyle \mathbf {v} } L ( u ) {\displaystyle L(\mathbf {u} )} u ⋅ v = | u | | v | cos ( θ ) = | u | proj ( v | u ) {\displaystyle \mathbf {u} \cdot \mathbf {v} =|\mathbf {u} ||\mathbf {v} |\cos(\theta )=|\mathbf {u} |{\text{proj}}(\mathbf {v} |\mathbf {u} )} proj ( v | u ) = | v | cos ( θ ) {\displaystyle {\text{proj}}(\mathbf {v} |\mathbf {u} )=|\mathbf {v} |\cos(\theta )} v {\displaystyle \mathbf {v} } L ( u ) {\displaystyle L(\mathbf {u} )} u {\displaystyle \mathbf {u} } proj ( v | u ) {\displaystyle {\text{proj}}(\mathbf {v} |\mathbf {u} )} v {\displaystyle \mathbf {v} } u {\displaystyle \mathbf {u} } u ⋅ v = | u | proj ( v | u ) {\displaystyle \mathbf {u} \cdot \mathbf {v} =|\mathbf {u} |{\text{proj}}(\mathbf {v} |\mathbf {u} )} v {\displaystyle \mathbf {v} }
點積的雙線性現在使得推導
u ⋅ v = ( u x u y ) ⋅ ( v x v y ) {\displaystyle \mathbf {u} \cdot \mathbf {v} ={\begin{pmatrix}u_{x}\\u_{y}\end{pmatrix}}\cdot {\begin{pmatrix}v_{x}\\v_{y}\end{pmatrix}}} = ( u x ( 1 0 ) + u y ( 0 1 ) ) ⋅ ( v x ( 1 0 ) + v y ( 0 1 ) ) {\displaystyle =\left(u_{x}{\begin{pmatrix}1\\0\end{pmatrix}}+u_{y}{\begin{pmatrix}0\\1\end{pmatrix}}\right)\cdot \left(v_{x}{\begin{pmatrix}1\\0\end{pmatrix}}+v_{y}{\begin{pmatrix}0\\1\end{pmatrix}}\right)} = ( ( u x ( 1 0 ) + u y ( 0 1 ) ) ⋅ ( 1 0 ) ) v x + ( ( u x ( 1 0 ) + u y ( 0 1 ) ) ⋅ ( 0 1 ) ) v y {\displaystyle =\left(\left(u_{x}{\begin{pmatrix}1\\0\end{pmatrix}}+u_{y}{\begin{pmatrix}0\\1\end{pmatrix}}\right)\cdot {\begin{pmatrix}1\\0\end{pmatrix}}\right)v_{x}+\left(\left(u_{x}{\begin{pmatrix}1\\0\end{pmatrix}}+u_{y}{\begin{pmatrix}0\\1\end{pmatrix}}\right)\cdot {\begin{pmatrix}0\\1\end{pmatrix}}\right)v_{y}} = ( ( 1 0 ) ⋅ ( 1 0 ) ) u x v x + ( ( 0 1 ) ⋅ ( 1 0 ) ) u y v x + ( ( 1 0 ) ⋅ ( 0 1 ) ) u x v y + ( ( 0 1 ) ⋅ ( 0 1 ) ) u y v y {\displaystyle =\left({\begin{pmatrix}1\\0\end{pmatrix}}\cdot {\begin{pmatrix}1\\0\end{pmatrix}}\right)u_{x}v_{x}+\left({\begin{pmatrix}0\\1\end{pmatrix}}\cdot {\begin{pmatrix}1\\0\end{pmatrix}}\right)u_{y}v_{x}+\left({\begin{pmatrix}1\\0\end{pmatrix}}\cdot {\begin{pmatrix}0\\1\end{pmatrix}}\right)u_{x}v_{y}+\left({\begin{pmatrix}0\\1\end{pmatrix}}\cdot {\begin{pmatrix}0\\1\end{pmatrix}}\right)u_{y}v_{y}} = 1 u x v x + 0 u y v x + 0 u x v y + 1 u y v y {\displaystyle =1u_{x}v_{x}+0u_{y}v_{x}+0u_{x}v_{y}+1u_{y}v_{y}} = u x v x + u y v y {\displaystyle =u_{x}v_{x}+u_{y}v_{y}}
因此 u ⋅ v = u x v x + u y v y {\displaystyle \mathbf {u} \cdot \mathbf {v} =u_{x}v_{x}+u_{y}v_{y}}
單位向量 是指長度為 1 的向量。向量 u 的單位向量 是指與 u {\displaystyle \mathbf {u} }
單位向量 u {\displaystyle \mathbf {u} } 標準化 。如標量乘法 中所述,將向量乘以常數 c {\displaystyle c} c {\displaystyle c} u {\displaystyle \mathbf {u} } u {\displaystyle \mathbf {u} }
w = u | u | {\displaystyle \mathbf {w} ={\frac {\mathbf {u} }{|\mathbf {u} |}}} ,其中
w {\displaystyle \mathbf {w} } 是
u {\displaystyle \mathbf {u} } 的單位向量。
單位向量 的一個特例是標準單位向量 i , j {\displaystyle \mathbf {i} ,\mathbf {j} } i {\displaystyle \mathbf {i} } x {\displaystyle x} j {\displaystyle \mathbf {j} } y {\displaystyle y}
i = ( 1 0 ) {\displaystyle \mathbf {i} ={\binom {1}{0}}}
j = ( 0 1 ) {\displaystyle \mathbf {j} ={\binom {0}{1}}}
使用標量乘法和向量加法規則,我們可以用不同的方式表達向量。
( x y ) = x i + y j {\displaystyle {\binom {x}{y}}=x\mathbf {i} +y\mathbf {j} } 如果我們把這個方程解出來,它是有意義的。將 x {\displaystyle x} i {\displaystyle \mathbf {i} } ( x 0 ) {\displaystyle {\binom {x}{0}}} y {\displaystyle y} j {\displaystyle \mathbf {j} } ( 0 y ) {\displaystyle {\binom {0}{y}}} ( x y ) {\displaystyle {\binom {x}{y}}} i , j {\displaystyle \mathbf {i} ,\mathbf {j} }
有時需要將向量 u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} } u ∥ {\displaystyle \mathbf {u} _{\parallel }} u ⊥ {\displaystyle \mathbf {u} _{\perp }}
由於 u ∥ {\displaystyle \mathbf {u} _{\parallel }} | u | ⋅ cos ( θ ) {\displaystyle |\mathbf {u} |\cdot \cos(\theta )} u ⊥ {\displaystyle \mathbf {u} _{\perp }} u ∥ {\displaystyle \mathbf {u} _{\parallel }}
u ∥ = | u | ∗ ( u ⋅ v ) ( | u | | v | ) ∗ v | v | = u ⋅ v | v | 2 v {\displaystyle \mathbf {u_{\parallel }} =|\mathbf {u} |*{\frac {(\mathbf {u} \cdot \mathbf {v} )}{(|\mathbf {u} ||\mathbf {v} |)}}*{\frac {\mathbf {v} }{|\mathbf {v} |}}={\frac {\mathbf {u} \cdot \mathbf {v} }{|\mathbf {v} |^{2}}}\mathbf {v} }
和
u ⊥ = u − u ∥ {\displaystyle \mathbf {u} _{\perp }=\mathbf {u} -\mathbf {u} _{\parallel }} 向量的長度由向量與其自身的點積給出,並且 θ = 0 r a d {\displaystyle \theta =0\ rad}
u ⋅ u = | u | | u | cos ( θ ) = | u | 2 {\displaystyle \mathbf {u} \cdot \mathbf {u} =|\mathbf {u} ||\mathbf {u} |\cos(\theta )=|\mathbf {u} |^{2}} 如果兩個向量的夾角 θ {\displaystyle \theta } π 2 {\displaystyle {\tfrac {\pi }{2}}} u = ( u x u y ) {\displaystyle \mathbf {u} ={\begin{pmatrix}u_{x}\\u_{y}\end{pmatrix}}}
v = ( − u y u x ) = − ( u y − u x ) {\displaystyle \mathbf {v} ={\begin{pmatrix}-u_{y}\\u_{x}\end{pmatrix}}=-{\begin{pmatrix}u_{y}\\-u_{x}\end{pmatrix}}} 極座標是另一種二維座標系,當旋轉很重要時,它通常很有用。 我們不指定沿 x {\displaystyle x} y {\displaystyle y} r {\displaystyle r} θ {\displaystyle \theta }
觀察這個圖,我們可以看到 x , y {\displaystyle x,y} r {\displaystyle r} θ {\displaystyle \theta }
x = r cos ( θ ) r = x 2 + y 2 y = r sin ( θ ) θ = arctan ( y x ) {\displaystyle {\begin{matrix}x=r\cos(\theta )&r={\sqrt {x^{2}+y^{2}}}\\y=r\sin(\theta )&\theta =\arctan \left({\frac {y}{x}}\right)\end{matrix}}} 由於 tan-1 是多值的,因此必須注意選擇正確的值。
就像笛卡爾座標系中指向 x {\displaystyle x} y {\displaystyle y} r {\displaystyle r} θ {\displaystyle \theta }
我們將這些向量稱為 r ^ {\displaystyle {\hat {\mathbf {r} }}} θ ^ {\displaystyle {\hat {\boldsymbol {\theta }}}}
再次,從圖中可以看出,
i = r ^ cos ( θ ) − θ ^ sin ( θ ) r ^ = x r i + y r j j = r ^ sin ( θ ) + θ ^ cos ( θ ) θ ^ = − y r i + x r j {\displaystyle {\begin{matrix}\mathbf {i} ={\hat {\mathbf {r} }}\cos(\theta )-{\hat {\boldsymbol {\theta }}}\sin(\theta )&{\hat {\mathbf {r} }}={\frac {x}{r}}\mathbf {i} +{\frac {y}{r}}\mathbf {j} \\\mathbf {j} ={\hat {\mathbf {r} }}\sin(\theta )+{\hat {\boldsymbol {\theta }}}\cos(\theta )&{\hat {\boldsymbol {\theta }}}=-{\frac {y}{r}}\mathbf {i} +{\frac {x}{r}}\mathbf {j} \end{matrix}}}
我們之前討論過的二維笛卡爾座標系可以很容易地擴充套件到三維,方法是新增一個額外的值: z {\displaystyle z} ( x , y ) {\displaystyle (x,y)} z {\displaystyle z}
3D座標軸。 與二維座標系中的兩個座標軸類似,空間中有三個座標平面 。分別是 x y {\displaystyle xy} 平面 , y z {\displaystyle yz} 平面 和 x z {\displaystyle xz} 平面 。每個平面都是包含名稱中提到的兩個軸的“紙張”。例如, y z {\displaystyle yz} y {\displaystyle y} z {\displaystyle z} x {\displaystyle x}
空間中的座標平面。 因此,向量可以透過簡單地新增 z {\displaystyle z}
u = ( x y z ) {\displaystyle \mathbf {u} ={\begin{pmatrix}x\\y\\z\end{pmatrix}}} 為了方便標準形式的表示,我們新增另一個標準單位向量
k = ( 0 0 1 ) {\displaystyle \mathbf {k} ={\begin{pmatrix}0\\0\\1\end{pmatrix}}} 同樣,兩種形式(分量形式和標準形式)是等價的。
( 1 2 3 ) = 1 i + 2 j + 3 k {\displaystyle {\begin{pmatrix}1\\2\\3\end{pmatrix}}=1\mathbf {i} +2\mathbf {j} +3\mathbf {k} } 模長 : 三維空間中的模長與二維空間中的模長相同,只是在被開方數中添加了一個 z {\displaystyle z}
| u | = u x 2 + u y 2 + u z 2 {\displaystyle |\mathbf {u} |={\sqrt {u_{x}^{2}+u_{y}^{2}+u_{z}^{2}}}} 極座標系擴充套件到三維空間,有兩種不同的座標系,即圓柱座標系和球座標系,兩者都包含二維或平面極座標作為子集。本質上,圓柱座標系透過新增一個額外的距離座標來擴充套件極座標,而球座標系則新增一個額外的角度座標。
用圓柱座標繪製的點。 圓柱座標系 是一個座標系,它本質上透過新增一個測量點在平面以上高度的第三個座標來擴充套件二維極座標系,類似於笛卡爾座標系擴充套件到三維空間的方式。第三個座標通常表示為 h {\displaystyle h} z {\displaystyle z} ( r , θ , h ) {\displaystyle (r,\theta ,h)} ( r , θ , z ) {\displaystyle (r,\theta ,z)}
三個圓柱座標可以透過以下公式轉換為笛卡爾座標
x = r cos ( θ ) y = r sin ( θ ) z = h {\displaystyle {\begin{aligned}x&=r\cos(\theta )\\y&=r\sin(\theta )\\z&=h\end{aligned}}} 用球座標繪製的點 極座標也可以擴充套件到三維空間,使用座標 ( ρ , ϕ , θ ) {\displaystyle (\rho ,\phi ,\theta )} ( ρ , φ , θ ) {\displaystyle (\rho ,\varphi ,\theta )} ρ {\displaystyle \rho } ϕ {\displaystyle \phi } φ {\displaystyle \varphi } z {\displaystyle z} θ {\displaystyle \theta } x {\displaystyle x} δ {\displaystyle \delta } ϕ {\displaystyle \phi } δ = 90 ∘ − ϕ {\displaystyle \delta =90^{\circ }-\phi } l {\displaystyle l} l = θ − 180 ∘ {\displaystyle l=\theta -180^{\circ }}
三個球面座標轉換為笛卡爾座標如下:
x = ρ sin ( ϕ ) cos ( θ ) y = ρ sin ( ϕ ) sin ( θ ) z = ρ cos ( ϕ ) {\displaystyle {\begin{aligned}x&=\rho \sin(\phi )\cos(\theta )\\y&=\rho \sin(\phi )\sin(\theta )\\z&=\rho \cos(\phi )\end{aligned}}} ρ = x 2 + y 2 + z 2 {\displaystyle \rho ={\sqrt {x^{2}+y^{2}+z^{2}}}} θ = arctan ( y x ) {\displaystyle \theta =\arctan \left({\frac {y}{x}}\right)} ϕ = arccos ( z ρ ) {\displaystyle \phi =\arccos \left({\frac {z}{\rho }}\right)} 兩個向量的叉積是一個 行列式
u × v = | i j k u x u y u z v x v y v z | {\displaystyle \mathbf {u} \times \mathbf {v} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\end{vmatrix}}} 它也是一個偽向量 .
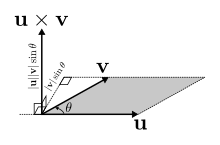
兩個向量的叉積與這兩個向量都正交。叉積的大小是兩個向量的大小和它們之間夾角的正弦的乘積。
| u × v | = | u | | v | sin ( θ ) {\displaystyle |\mathbf {u} \times \mathbf {v} |=|\mathbf {u} ||\mathbf {v} |\sin(\theta )} 這個大小是這兩個向量定義的平行四邊形的面積。
叉積是線性的 和反交換的 。對於任何數字 a , b {\displaystyle a,b}
u × ( a v + b w ) = a u × v + b u × w u × v = − v × u {\displaystyle \mathbf {u} \times \left(a\mathbf {v} +b\mathbf {w} \right)=a\mathbf {u} \times \mathbf {v} +b\mathbf {u} \times \mathbf {w} \qquad \mathbf {u} \times \mathbf {v} =-\mathbf {v} \times \mathbf {u} } 如果兩個向量都指向同一個方向,它們的叉積為 0。
向量 u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} } 從以下叉積定義開始: u × v = ( | u | | v | sin θ ) n ^ {\displaystyle \mathbf {u} \times \mathbf {v} =(|\mathbf {u} ||\mathbf {v} |\sin \theta ){\hat {\mathbf {n} }}} n ^ {\displaystyle {\hat {\mathbf {n} }}} u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} } θ {\displaystyle \theta } u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} } n ^ {\displaystyle {\hat {\mathbf {n} }}}
公式 u × v = ( u y v z − u z v y ) i + ( u z v x − u x v z ) j + ( u x v y − u y v x ) k {\displaystyle \mathbf {u} \times \mathbf {v} =(u_{y}v_{z}-u_{z}v_{y})\mathbf {i} +(u_{z}v_{x}-u_{x}v_{z})\mathbf {j} +(u_{x}v_{y}-u_{y}v_{x})\mathbf {k} }
保持 u {\displaystyle \mathbf {u} } u × v {\displaystyle \mathbf {u} \times \mathbf {v} } v {\displaystyle \mathbf {v} }
保持 v {\displaystyle \mathbf {v} } u × v {\displaystyle \mathbf {u} \times \mathbf {v} } u {\displaystyle \mathbf {u} } 從定義 u × v = ( | u | | v | sin θ ) n ^ {\displaystyle \mathbf {u} \times \mathbf {v} =(|\mathbf {u} ||\mathbf {v} |\sin \theta ){\hat {\mathbf {n} }}} u × v = − v × u {\displaystyle \mathbf {u} \times \mathbf {v} =-\mathbf {v} \times \mathbf {u} } n ^ {\displaystyle {\hat {\mathbf {n} }}} u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} } v {\displaystyle \mathbf {v} } u {\displaystyle \mathbf {u} } v {\displaystyle \mathbf {v} }
關於直線 L ( u ) {\displaystyle L(\mathbf {u} )} v {\displaystyle \mathbf {v} } u × v = ( | u | | v | sin θ ) n ^ = | u | rotate ( perp ( v | u ) | u ) {\displaystyle \mathbf {u} \times \mathbf {v} =(|\mathbf {u} ||\mathbf {v} |\sin \theta ){\hat {\mathbf {n} }}=|\mathbf {u} |{\textbf {rotate}}({\textbf {perp}}(\mathbf {v} |\mathbf {u} )|\mathbf {u} )}
perp ( v | u ) {\displaystyle {\textbf {perp}}(\mathbf {v} |\mathbf {u} )} v {\displaystyle \mathbf {v} } L ( u ) {\displaystyle L(\mathbf {u} )} u {\displaystyle \mathbf {u} } perp ( v | u ) = ( | v | sin θ ) m ^ {\displaystyle {\textbf {perp}}(\mathbf {v} |\mathbf {u} )=(|\mathbf {v} |\sin \theta ){\hat {\mathbf {m} }}} m ^ {\displaystyle {\hat {\mathbf {m} }}} perp ( v | u ) {\displaystyle {\textbf {perp}}(\mathbf {v} |\mathbf {u} )} rotate ( w | u ) {\displaystyle {\textbf {rotate}}(\mathbf {w} |\mathbf {u} )} w {\displaystyle \mathbf {w} } L ( u ) {\displaystyle L(\mathbf {u} )} rotate ( m ^ | u ) = n ^ {\displaystyle {\textbf {rotate}}({\hat {\mathbf {m} }}|\mathbf {u} )={\hat {\mathbf {n} }}} 很容易觀察到 perp ( v | u ) {\displaystyle {\textbf {perp}}(\mathbf {v} |\mathbf {u} )} v {\displaystyle \mathbf {v} } u {\displaystyle \mathbf {u} } rotate ( w | u ) {\displaystyle {\textbf {rotate}}(\mathbf {w} |\mathbf {u} )} w {\displaystyle \mathbf {w} } u {\displaystyle \mathbf {u} } u × v = ( | u | | v | sin θ ) n ^ = | u | rotate ( perp ( v | u ) | u ) {\displaystyle \mathbf {u} \times \mathbf {v} =(|\mathbf {u} ||\mathbf {v} |\sin \theta ){\hat {\mathbf {n} }}=|\mathbf {u} |{\textbf {rotate}}({\textbf {perp}}(\mathbf {v} |\mathbf {u} )|\mathbf {u} )} v {\displaystyle \mathbf {v} }
叉積的雙線性現在使得推導成為可能
u × v = ( u x i + u y j + u z k ) × ( v x i + v y j + v z k ) {\displaystyle \mathbf {u} \times \mathbf {v} =(u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\times (v_{x}\mathbf {i} +v_{y}\mathbf {j} +v_{z}\mathbf {k} )} = v x ( ( u x i + u y j + u z k ) × i ) + v y ( ( u x i + u y j + u z k ) × j ) + v z ( ( u x i + u y j + u z k ) × k ) {\displaystyle =v_{x}((u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\times \mathbf {i} )+v_{y}((u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\times \mathbf {j} )+v_{z}((u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} )\times \mathbf {k} )} = u x v x ( i × i ) + u y v x ( j × i ) + u z v x ( k × i ) + u x v y ( i × j ) + u y v y ( j × j ) + u z v y ( k × j ) + u x v z ( i × k ) + u y v z ( j × k ) + u z v z ( k × k ) {\displaystyle =u_{x}v_{x}(\mathbf {i} \times \mathbf {i} )+u_{y}v_{x}(\mathbf {j} \times \mathbf {i} )+u_{z}v_{x}(\mathbf {k} \times \mathbf {i} )+u_{x}v_{y}(\mathbf {i} \times \mathbf {j} )+u_{y}v_{y}(\mathbf {j} \times \mathbf {j} )+u_{z}v_{y}(\mathbf {k} \times \mathbf {j} )+u_{x}v_{z}(\mathbf {i} \times \mathbf {k} )+u_{y}v_{z}(\mathbf {j} \times \mathbf {k} )+u_{z}v_{z}(\mathbf {k} \times \mathbf {k} )} = u x v y 0 + u y v x ( − k ) + u z v x j + u x v y k + u y v y 0 + u z v y ( − i ) + u x v z ( − j ) + u y v z i + u z v z 0 {\displaystyle =u_{x}v_{y}\mathbf {0} +u_{y}v_{x}(-\mathbf {k} )+u_{z}v_{x}\mathbf {j} +u_{x}v_{y}\mathbf {k} +u_{y}v_{y}\mathbf {0} +u_{z}v_{y}(-\mathbf {i} )+u_{x}v_{z}(-\mathbf {j} )+u_{y}v_{z}\mathbf {i} +u_{z}v_{z}\mathbf {0} } = ( u y v z − u z v y ) i + ( u z v x − u x v z ) j + ( u x v y − u y v x ) k {\displaystyle =(u_{y}v_{z}-u_{z}v_{y})\mathbf {i} +(u_{z}v_{x}-u_{x}v_{z})\mathbf {j} +(u_{x}v_{y}-u_{y}v_{x})\mathbf {k} }
因此 u × v = ( u y v z − u z v y ) i + ( u z v x − u x v z ) j + ( u x v y − u y v x ) k {\displaystyle \mathbf {u} \times \mathbf {v} =(u_{y}v_{z}-u_{z}v_{y})\mathbf {i} +(u_{z}v_{x}-u_{x}v_{z})\mathbf {j} +(u_{x}v_{y}-u_{y}v_{x})\mathbf {k} }
如果我們有三個向量,我們可以用兩種方法將它們組合起來,一個三重標量積,
u ⋅ ( v × w ) {\displaystyle \mathbf {u} \cdot (\mathbf {v} \times \mathbf {w} )} 以及一個三重向量積
u × ( v × w ) {\displaystyle \mathbf {u} \times (\mathbf {v} \times \mathbf {w} )} 三重標量積是一個行列式
u ⋅ ( v × w ) = | u x u y u z v x v y v z w x w y w z | {\displaystyle \mathbf {u} \cdot (\mathbf {v} \times \mathbf {w} )={\begin{vmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{vmatrix}}} 如果三個向量從原點看去是順時針排列的,那麼該積的符號為正。如果它們是逆時針排列的,那麼符號為負。
叉積和點積的順序無關緊要。
u ⋅ ( v × w ) = ( u × v ) ⋅ w {\displaystyle \mathbf {u} \cdot (\mathbf {v} \times \mathbf {w} )=(\mathbf {u} \times \mathbf {v} )\cdot \mathbf {w} } 無論哪種方式,該積的絕對值都是由三個向量 u , v , w {\displaystyle \mathbf {u} ,\mathbf {v} ,\mathbf {w} }
三重向量積可以簡化。
u × ( v × w ) = ( u ⋅ w ) v − ( u ⋅ v ) w {\displaystyle \mathbf {u} \times (\mathbf {v} \times \mathbf {w} )=(\mathbf {u} \cdot \mathbf {w} )\mathbf {v} -(\mathbf {u} \cdot \mathbf {v} )\mathbf {w} } 這種形式更容易進行計算。
三重向量積不是 結合的。
u × ( v × w ) ≠ ( u × v ) × w {\displaystyle \mathbf {u} \times (\mathbf {v} \times \mathbf {w} )\neq (\mathbf {u} \times \mathbf {v} )\times \mathbf {w} } 在某些特殊情況下,兩邊相等,但一般來說,括號很重要。它們不能省略。
我們將使用 r {\displaystyle \mathbf {r} }
向量 a {\displaystyle \mathbf {a} } b {\displaystyle \mathbf {b} }
r = s a + b {\displaystyle \mathbf {r} =s\mathbf {a} +\mathbf {b} } 這是一個引數方程 。位置是根據引數 s {\displaystyle s}
任何兩個向量的線性組合, a , b {\displaystyle \mathbf {a} ,\mathbf {b} }
r = s a + t b + c {\displaystyle \mathbf {r} =s\mathbf {a} +t\mathbf {b} +\mathbf {c} } 如果我們選擇 a , b {\displaystyle \mathbf {a} ,\mathbf {b} } 標準正交 向量(即直角單位向量),那麼 s , t {\displaystyle s,t}
這些引數方程可以擴充套件到更高維度。
我們不提供直線和平面的引數方程,而是使用約束條件。例如,對於 x y {\displaystyle xy} z = 0 {\displaystyle z=0}
對於透過原點的平面,垂直於平面的單個向量, n {\displaystyle \mathbf {n} }
r ⋅ n = 0 {\displaystyle \mathbf {r} \cdot \mathbf {n} =0} 是透過原點的平面,垂直於 n {\displaystyle \mathbf {n} }
對於不透過原點的平面,我們得到
( r − a ) ⋅ n = 0 r ⋅ n = a ⋅ n {\displaystyle (\mathbf {r} -\mathbf {a} )\cdot \mathbf {n} =0\qquad \mathbf {r} \cdot \mathbf {n} =\mathbf {a} \cdot \mathbf {n} } 一條直線位於兩個平面的交線上,因此它必須滿足兩個平面的約束條件,即
r ⋅ n = a r ⋅ m = b {\displaystyle \mathbf {r} \cdot \mathbf {n} =a\qquad \mathbf {r} \cdot \mathbf {m} =b} 這些約束方程也可以擴充套件到更高維度。
向量值函式是函式,它們不提供結果標量值,而是提供結果向量值。它們有助於建立方向和向量場,因此在物理學中用於幫助視覺化電場、磁場和許多其他型別的場。它們具有以下形式
F ( t ) = ( a 1 ( t ) ⋮ a n ( t ) ) {\displaystyle \mathbf {F(t)} ={\begin{pmatrix}\mathbf {a_{1}(t)} \\\vdots \\\mathbf {a_{n}(t)} \end{pmatrix}}}
簡單來說,向量值函式的極限是其各個部分的極限。
證明 假設 lim t → c F ( t ) = L = ( a 1 ⋮ a n ) {\displaystyle \lim _{t\to c}\mathbf {F} (t)=\mathbf {L} ={\begin{pmatrix}\mathbf {a_{1}} \\\vdots \\\mathbf {a_{n}} \end{pmatrix}}}
因此,對於任何 ε > 0 {\displaystyle \varepsilon >0} ϕ > 0 {\displaystyle \phi >0}
0 < | t − c | < ϕ ⟹ | F ( t ) − L | < ε {\displaystyle 0<|t-c|<\phi \implies |\mathbf {F} (t)-\mathbf {L} |<\varepsilon }
但根據三角不等式 | a 1 | ≤ | F | ≤ | a 1 | + ⋯ + | a n | {\displaystyle |a_{1}|\leq |\mathbf {F} |\leq |a_{1}|+\cdots +|a_{n}|}
| a 1 ( t ) − a 1 | ≤ | F ( t ) − L | {\displaystyle |a_{1}(t)-a_{1}|\leq |\mathbf {F} (t)-\mathbf {L} |}
所以
0 < | t − c | < ϕ ⟹ | a 1 ( t ) − a 1 | < ε {\displaystyle 0<|t-c|<\phi \implies |a_{1}(t)-a_{1}|<\varepsilon }
因此 lim t → c a 1 ( t ) = a 1 {\displaystyle \lim _{t\to c}a_{1}(t)=a_{1}}
類似的論據可以應用於所有部分 a n ( t ) {\displaystyle a_{n}(t)}
現在令 lim t → c F ( t ) = L = ( a 1 ⋮ a n ) {\displaystyle \lim _{t\to c}\mathbf {F} (t)=\mathbf {L} ={\begin{pmatrix}\mathbf {a_{1}} \\\vdots \\\mathbf {a_{n}} \end{pmatrix}}} ε > 0 {\displaystyle \varepsilon >0} ϕ > 0 {\displaystyle \phi >0} 0 < | t − c | < ϕ {\displaystyle 0<|t-c|<\phi }
| a n ( t ) − a n | < ε n {\displaystyle |a_{n}(t)-a_{n}|<{\frac {\varepsilon }{n}}}
那麼
0 < | t − c | < ϕ ⟹ | F ( t ) − L | ≤ ε 1 n + ⋯ + ε n n = ε {\displaystyle 0<|t-c|<\phi \implies |\mathbf {F} (t)-\mathbf {L} |\leq {\frac {\varepsilon _{1}}{n}}+\cdots +{\frac {\varepsilon _{n}}{n}}=\varepsilon }
因此
lim t → c F ( t ) = L = ( a 1 ⋮ a n ) = ( lim t → c a 1 ( t ) ⋮ lim t → c a n ( t ) ) {\displaystyle \lim _{t\to c}\mathbf {F} (t)=\mathbf {L} ={\begin{pmatrix}\mathbf {a_{1}} \\\vdots \\\mathbf {a_{n}} \end{pmatrix}}={\begin{pmatrix}\lim \limits _{t\to c}\mathbf {a_{1}(t)} \\\vdots \\\lim \limits _{t\to c}\mathbf {a_{n}(t)} \end{pmatrix}}}
由此,我們可以建立一個向量值函式導數的精確定義
F ′ ( t ) = lim h → 0 F ( t + h ) − F ( t ) h = ( a 1 ( t ) ⋮ a n ( t ) ) = lim h → 0 ( a 1 ( t + h ) ⋮ a n ( t + h ) ) − ( a 1 ( t ) ⋮ a n ( t ) ) h = ( lim h → 0 a 1 ( t + h ) − a 1 ( t ) h ⋮ lim h → 0 a n ( t + h ) − a n ( t ) h ) {\displaystyle {\begin{aligned}\mathbf {F} '(t)&=\lim _{h\to 0}{\frac {\mathbf {F} (t+h)-\mathbf {F} (t)}{h}}={\begin{pmatrix}\mathbf {a_{1}(t)} \\\vdots \\\mathbf {a_{n}(t)} \end{pmatrix}}\\&=\lim _{h\to 0}{\frac {{\begin{pmatrix}\mathbf {a_{1}(t+h)} \\\vdots \\\mathbf {a_{n}(t+h)} \end{pmatrix}}-{\begin{pmatrix}\mathbf {a_{1}(t)} \\\vdots \\\mathbf {a_{n}(t)} \end{pmatrix}}}{h}}\\&={\begin{pmatrix}\lim \limits _{h\to 0}{\dfrac {a_{1}(t+h)-a_{1}(t)}{h}}\\\vdots \\\lim \limits _{h\to 0}{\dfrac {a_{n}(t+h)-a_{n}(t)}{h}}\end{pmatrix}}\end{aligned}}}
最後一步是透過我們剛對極限所做的操作來完成的。
根據微積分基本定理,積分可以應用於向量的分量。
換句話說:向量函式的極限是其各個部分的極限,向量函式的導數是其各個部分的導數,向量函式的積分是其各個部分的積分。
假設我們有一個向量值函式,它從原點開始,隨著其自變數的變化,向量所指向的點會描繪出一條路徑。
我們將這個向量稱為 r ( t ) {\displaystyle \mathbf {r} (t)} 位置向量 。
如果 r {\displaystyle \mathbf {r} }
r ( t + h ) − r ( t ) {\displaystyle \mathbf {r} (t+h)-\mathbf {r} (t)} r ′ ( t ) = v ( t ) {\displaystyle \mathbf {r} '(t)=\mathbf {v} (t)} v ( t ) {\displaystyle \mathbf {v} (t)} | v ( t ) | {\displaystyle |\mathbf {v} (t)|} r ″ ( t ) = v ′ ( t ) = a ( t ) {\displaystyle \mathbf {r} ''(t)=\mathbf {v} '(t)=\mathbf {a} (t)} a ( t ) {\displaystyle \mathbf {a} (t)} 有時還會用到另一個向量,稱為曲率向量。
用來求曲率向量的向量 T ( t ) {\displaystyle \mathbf {T} (t)} v ( t ) | v ( t ) | {\displaystyle {\frac {\mathbf {v} (t)}{|\mathbf {v} (t)|}}} v ^ {\displaystyle \mathbf {\hat {v}} }
然後,該向量的法向量 N {\displaystyle \mathbf {N} } T ′ ( t ) | v ( t ) | {\displaystyle {\frac {\mathbf {T} '(t)}{|\mathbf {v} (t)|}}}
我們可以透過取點積來驗證這一點
T ⋅ N = 0 {\displaystyle \mathbf {T} \cdot \mathbf {N} =0}
還要注意 | v ( t ) | = d s d t {\displaystyle |\mathbf {v} (t)|={\frac {ds}{dt}}}
和
T ( t ) = v | v | = d r d t d s d t = d r d s {\displaystyle \mathbf {T} (t)={\frac {v}{|v|}}={\frac {\frac {dr}{dt}}{\frac {ds}{dt}}}={\frac {dr}{ds}}}
和
N = T ′ ( t ) | v ( t ) | = d T d t d s d t = d T d s {\displaystyle \mathbf {N} ={\frac {\mathbf {T} '(t)}{|\mathbf {v} (t)|}}={\frac {\frac {dT}{dt}}{\frac {ds}{dt}}}={\frac {dT}{ds}}}
然後,我們實際上可以驗證
d d s ( T ⋅ T ) = d d s ( 1 ) {\displaystyle {\frac {d}{ds}}(\mathbf {T} \cdot \mathbf {T} )={\frac {d}{ds}}(1)}
d T d s ⋅ T + T ⋅ d T d s = 0 {\displaystyle {\frac {dT}{ds}}\cdot \mathbf {T} +\mathbf {T} \cdot {\frac {dT}{ds}}=0}
2 T ⋅ d T d s = 0 {\displaystyle 2\mathbf {T} \cdot {\frac {dT}{ds}}=0}
T ⋅ d T d s = 0 {\displaystyle \mathbf {T} \cdot {\frac {dT}{ds}}=0}
T ⋅ N = 0 {\displaystyle \mathbf {T} \cdot \mathbf {N} =0}
因此 N {\displaystyle \mathbf {N} } T {\displaystyle \mathbf {T} }
這導致了 **單位法向量** d T d s | d T d s | {\displaystyle {\frac {\frac {dT}{ds}}{\left|{\frac {dT}{ds}}\right|}}} ( | d T d s | ) − 1 {\displaystyle (|{\frac {dT}{ds}}|)^{-1}}
唯一沒有提到的就是三維曲線中出現的副法線 T × N = B {\displaystyle \mathbf {T} \times \mathbf {N} =\mathbf {B} }