電路理論/卷積積分/示例/example49/VL

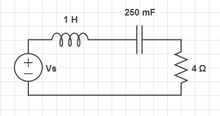
串聯 LRC 電路 ... 求電阻兩端的電壓

已知源電壓為 (2t-3t²)，求電阻兩端的電壓。

這是 V_L 解。

概述

傳遞函式

$H(s)={\frac {V_{L}}{V_{S}}}={\frac {s}{4+s+{\frac {1}{0.25s}}}}$

simplify(s/(4 + s + 1/(0.25*s)))

$H(s)={\frac {s^{2}}{s^{2}+4s+4}}$

齊次解

solve(s^2 + 4.0*s + 4.0,s)

在 s = -2 處有兩個相等的根，因此解的形式為

$V_{L_{h}}(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

特解

在長時間連線到單位階躍函式源後，電感器短路，電容器開路。所有壓降都在電容器上。

$V_{L_{p}}=0$

這也意味著 C₁ 必須為零。

初始條件

到目前為止，完整的方程是

$V_{L}(t)=Ae^{-2t}+Bte^{-2t}$

初始電壓全部跨越電感器。

$V_{L}(0)=1=A$

$A=1$

此時將不得不進行積分 ... 以得到電流。沒有其他方法可以使用已知的初始條件：電流（最初為零）和 V_C（最初為零）。將不得不引入積分常數，然後對其進行評估。更容易出錯，更復雜，因此從其他方面重新開始。

$i(t)={\frac {1}{L}}\int _{0}^{t}V_{L}(t)dt=\int _{0}^{t}(e^{-2x}-B(x)e^{-2x})dx$

f := (exp(-2*x) - B*x*exp(-2*x));
S :=int(f,x=0..t)

$i(t)=B*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}}+C_{1}$

$i(0)=0=C_{1}$

好的，所以 C₁ 等於零。現在需要找到 B。透過再次積分得到 V_C 來找到 B

$V_{C}(t)={\frac {1}{C}}\int _{0}^{t}i(t)dt=4*\int _{0}^{t}(B*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}})dx$

f := (4*(B*(exp(-2*x)*(2*x+1)/4 -1/4) - exp(-2*x)/2 + 1/2));
S :=int(f,x=0..t)

$V_{C}(t)=B+2t+e^{-2t}-Bt-Be^{-2t}-Bte^{-2t}-1+C_{1}$

$V_{C}(0)=0=B+1-B-1+C_{1}$

$C_{1}=0$

但這仍然無法幫助我們找到 B。假設 B = 2，因為如果 V_C 要收斂到 1，則 (2t-Bt) 必須等於零。然後看看 V_C(∞) 是否等於 1

$V_{C}(t)=2+e^{-2t}-2e^{-2t}-2te^{-2t}-1$

當 t = ∞ 時，2te^-2t 項的值是多少？

limit(B*t*exp(-t),t = infinity)

Mupad 說 0。

$V_{C}(\infty )=2-1=1$

是的！B = 2 可行……看起來是唯一可行的……所以

$i(t)=2*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}}=te^{-2t}$

simplify(2*(exp(-2*t)(2*t+1)/4-1/4) - exp(-2*t)/2 + 1/2)

這意味著 V_R 是

$V_{R}(t)=4*i(t)=4te^{-2t}$

脈衝解

對上述進行求導得到

$V_{R}\delta (t)=4e^{-2t}-8te^{-2t}$

卷積積分

$V_{R}(t)=\int _{0}^{t}(4e^{-2(t-x)}-8(t-x)e^{-2(t-x)})(2x-3x^{2})dx$

f := (4*exp(-2*(t-x)) - 8*(t-x)exp(-2*(t-x)))*(2*x-3*x^2);
S :=int(f,x=0..t)

$V_{R}(t)=8-8e^{-2t}-10te^{-2t}-6t$

因為在很長一段時間後，V_R(t) 會變為 0 ... 且電容會斷開，所以不會有常數項。