電路理論/卷積積分/示例/example49/電流

串聯 LRC 電路... 找出電阻兩端的電壓

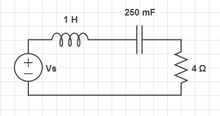
已知電源電壓為 (2t-3t²)，求電阻兩端的電壓。

這裡重點先求電流

傳遞函式

$H(s)={\frac {i}{V_{S}}}={\frac {1}{4+s+{\frac {1}{0.25s}}}}$

simplify(1/(4 + s + 1/(0.25*s)))

$H(s)={\frac {s}{s^{2}+4s+4}}$

齊次解

solve(s^2 + 4.0*s + 4.0,s)

在 s = -2 處有兩個相等的根，因此解的形式為

$i_{h}(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

特解

經過長時間連線到單位階躍函式電源後，電感器短路，電容器開路。所有壓降都出現在電容器兩端。電流為零。

$i_{p}=0$

初始條件

到目前為止，完整的方程是

$i(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

由於電感器的初始條件假設，串聯支路的初始電流為零。這意味著

$i(0)=0=A+C_{1}$

假設電容器兩端的初始電壓為零，則初始壓降必須出現在電感器兩端。

$V_{L}(t)=L{di(t) \over dt}=(-2A+B)e^{-2t}-2Bte^{-2t}$

$V_{L}(0)=1=-2A+B$

經過長時間後，電流仍然必須為零，因此

$C_{1}=0$

這意味著

$A=0$

$B=1$

$i(t)=te^{-2t}$

$V_{r}(t)=4te^{-2t}$

如果一開始為 V_r 寫傳遞函式，則傳遞函式的分子中會丟失 4。 4 不會出現在齊次解中。 在二階分析中，永遠不要為電阻寫傳遞函式。

脈衝解

對上述式子求導，得到

$V_{R}\delta (t)=4e^{-2t}-8te^{-2t}$

卷積積分

$V_{R}(t)=\int _{0}^{t}(4e^{-2(t-x)}-8(t-x)e^{-2(t-x)})(2x-3x^{2})dx$

f := (4*exp(-2*(t-x)) - 8*(t-x)exp(-2*(t-x)))*(2*x-3*x^2);
S :=int(f,x=0..t)

$V_{R}(t)=8-8e^{-2t}-10te^{-2t}-6t$

由於長時間後 V_R(t) = 0 ... 並且電容開啟，因此不會有任何常數。