電路理論/相量/示例/示例 10

用於示例 10 的並聯 RL 電路

假設電流源由$I_{s}(t)=120{\sqrt {2}}cos(377t+120^{\circ })$ 定義，求解所有其他電壓和電流，並檢查功率。

標註迴路和節點

用於分析的並聯 RL 電路標記圖

在並聯電路中，所有器件上的電壓都完全相同。

已知量、未知量和方程式

已知量：$I_{s},R,L$

未知量：$V_{s},i_{R},i_{L}$

方程式：$V_{s}(t)=R*i_{R}(t),V_{s}=L*{d \over dt}i_{L}(t),i_{R}(t)+i_{L}(t)-I_{s}(t)=0$

相量符號

mupad 嘗試進行一些相量代數運算...需要找到一種方法以符號形式求解矩形形式和極座標形式的實部和虛部，並找到數值評估的方法...m 檔案

時域

按順序評估端子關係

$i_{R}(t)={\frac {V_{s}}{R}}$

$i_{L}(t)=\int {\frac {V_{s}}{L}}dt$

代入這個等式

$I_{s}(t)=i_{R}(t)+i_{L}(t)$

$I_{s}(t)={\frac {V_{s}}{R}}+\int {\frac {V_{s}}{L}}dt$

為了讓數學家滿意，需要將其轉換為微分方程，所以對等式兩邊求導（不要讓他們看到你在這樣做）。

${dI_{s}(t) \over dt}={\frac {1}{R}}{dV_{s} \over dt}+{\frac {V_{s}}{L}}$

所以得到了一個可以求解的微分方程 $V_{s}$.

相量域

現在將這兩個運算轉換為相量域。

${I_{s}}(t)\rightarrow \mathbb {I} _{s}\rightarrow I_{m}\angle \phi$

$V_{s}(t)\rightarrow \mathbb {V} _{s}$

$\int V_{s}(t)dt\rightarrow {\frac {1}{j\omega }}\mathbb {V} _{s}$

所以

$\mathbb {I} _{s}={\frac {\mathbb {V} _{s}}{R}}+{\frac {\mathbb {V} _{s}}{j\omega L}}$ 或 $j\omega \mathbb {I} _{s}=j\omega {\frac {\mathbb {V} _{s}}{R}}+{\frac {\mathbb {V} _{s}}{L}}$

求解 $\mathbb {V} _{s}$

$\mathbb {V} _{s}={\frac {\mathbb {I} _{s}j\omega LR}{R+j\omega L}}$

轉換為矩形形式

$\mathbb {V} _{s}=\mathbb {I} _{s}*{\frac {\omega ^{2}L^{2}R+j\omega LR^{2}}{R^{2}+\omega ^{2}L^{2}}}$

轉換為極座標形式

$\mathbb {V} _{s}=\mathbb {I} _{s}{\frac {\sqrt {(\omega ^{2}L^{2}R)^{2}+(\omega LR^{2})^{2}}}{R^{2}+\omega ^{2}L^{2}}}\angle \arctan({\frac {R}{\omega L}})$

回到時域

$V_{s}(t)=I_{m}{\frac {\sqrt {(\omega ^{2}L^{2}R)^{2}+(\omega LR^{2})^{2}}}{R^{2}+\omega ^{2}L^{2}}}\cos(\phi +\arctan({\frac {R}{\omega L}}))$

會存在一個積分常數，但現在無法計算。

這是從一個微分方程推匯出的。

在將齊次解新增到上述特解後，將計算積分常數。

相量數值解

相量數值解將所有相量組合成矩形形式，然後直接轉為極座標形式。角度位於第三象限... m-檔案

時域

按順序評估端子關係

$i_{R}(t)={\frac {V_{s}}{10}}$

$i_{L}(t)=\int {\frac {V_{s}}{.01}}dt$

代入這個等式

$I_{s}(t)=i_{R}(t)+i_{L}(t)$

因此得到一個關於 $V_{s}$ 的微分方程，可以求解。

$I_{s}(t)={\frac {V_{s}}{10}}+\int {\frac {V_{s}}{.01}}dt$

相量域

將此代入從相量分析得到的符號時域解... 角度相同，位於第三象限... 這次為正數 ... m-檔案

選擇在時域進行計算

回到時域

$V_{s}(t)=120*{\sqrt {2}}{\frac {\sqrt {(377^{2}*.01^{2}*10)^{2}+(377*.01*10^{2})^{2}}}{10^{2}+377^{2}*.01^{2}}}\cos(377t+{\frac {2*\pi }{3}}+\arctan({\frac {10}{377*.01}}))$

$V_{s}(t)=599\cos(377t+3.30)$

$i_{R}(t)=59.9\cos(377t+3.30)$

$i_{L}(t)=159\sin(377t+3.30)=159\cos(377t+1.74)$

拉普拉斯符號

時域

按順序評估端子關係

$i_{R}(t)={\frac {V_{s}}{R}}$

$i_{L}(t)=\int {\frac {V_{s}}{L}}dt$

代入這個等式

$I_{s}(t)=i_{R}(t)+i_{L}(t)$

因此得到一個關於 $V_{s}$ 的微分方程，可以求解。

$I_{s}(t)={\frac {V_{s}}{R}}+\int {\frac {V_{s}}{L}}dt$

拉普拉斯域

現在將兩者都轉換為拉普拉斯域..

${I_{s}}(t)\rightarrow {\mathcal {L}}\left\{{I_{s}}(t)\right\}$

$V_{s}(t)\rightarrow {\mathcal {L}}\left\{V_{s}(t)\right\}$

$\int V_{s}(t)dt\rightarrow {\frac {1}{s}}{\mathcal {L}}\left\{V_{s}(t)\right\}\$

所以

${\mathcal {L}}\left\{{I_{s}}(t)\right\}={\frac {{\mathcal {L}}\left\{V_{s}(t)\right\}}{R}}+{\frac {{\mathcal {L}}\left\{V_{s}(t)\right\}}{sL}}$

求解${\mathcal {L}}\left\{V_{s}(t)\right\}$

${\mathcal {L}}\left\{V_{s}(t)\right\}=$${\frac {{{\mathcal {L}}\left\{{I_{s}}(t)\right\}}LsR}{R+sL}}$

此時拉普拉斯符號解必須停止。下一步取決於${{\mathcal {L}}\left\{{I_{s}}(t)\right\}}$的形式。

回到時域

在沒有${{\mathcal {L}}\left\{{I_{s}}(t)\right\}}$的情況下，這是無法完成的。函式${{\mathcal {L}}\left\{{I_{s}}(t)\right\}}$的形式決定了逆對映。

拉普拉斯數值

拉普拉斯解法與之前一樣存在相同的問題...常數...正弦項符號錯誤 m 檔案

時域

$I_{s}(t)=120{\sqrt {2}}cos(377t+2.09)$

$R=10$

$L=.01$

拉普拉斯域

${I_{s}}(t)\rightarrow {\mathcal {L}}\left\{{I_{s}}(t)\right\}={\mathcal {L}}\left\{120{\sqrt {2}}cos(377t+120^{\circ })\right\}=-{\frac {(170.0*(0.5*s+326.0))}{(s^{2}+142129)}}$

${\mathcal {L}}\left\{V_{s}(t)\right\}={\frac {\frac {-17.0*s*(0.5*s+326.0)}{(s^{2}+142129)}}{10+.01*s}}$

時域

$V_{s}(t)={\mathcal {L}}^{-1}\left\{i(t)\right\}=(-2.58)*e^{-{\frac {t}{.001}}}+97.2sin(377t)-591cos(377*t)$

答案比較

$V_{s}(t)=599\cos(377t-2.98)$ ... 來自相量域的數值解

$V_{s}(t)=599\cos(377t+3.30)$ ... 將其代入符號時域的解

相位角在第三象限的位置完全相同。

模擬

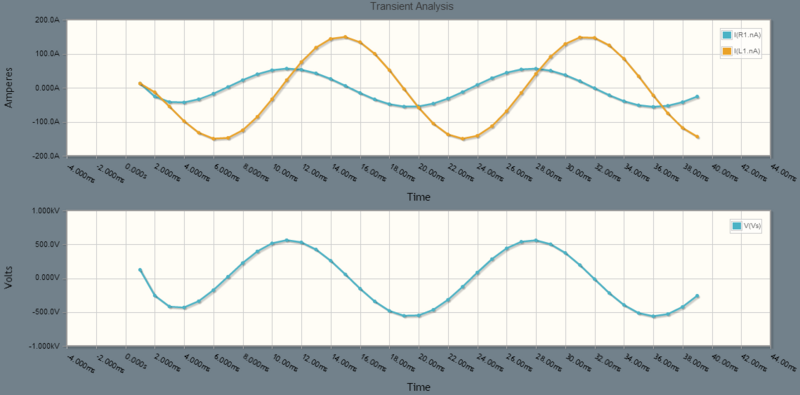
$i_{r}$ 與 $V_{s}$ 同相，正如預期的那樣。 $V_{s}$ 超前於 $i_{L}$（透過電感）${\frac {\pi }{2}}$，正如預期的那樣。一切似乎都圍繞著 0 伏特，因此沒有常數在起作用。

週期檢查

上面的週期看起來介於 16ms 和 17ms 之間，更接近 17ms。這與公式一致

$\omega =2\pi *f$

$f={\frac {\omega }{2\pi }}$

$T={\frac {1}{f}}={\frac {2\pi }{\omega }}={\frac {2\pi }{377}}=16.7ms$

幅值檢查

V_s 的幅值超過 500 伏特……雖然可能不到 600 伏特。

暫態響應檢查

一切都從零開始。這意味著只有模擬視窗的中間到右側才能顯示我們可以與計算值進行比較的穩態資訊。

相位檢查

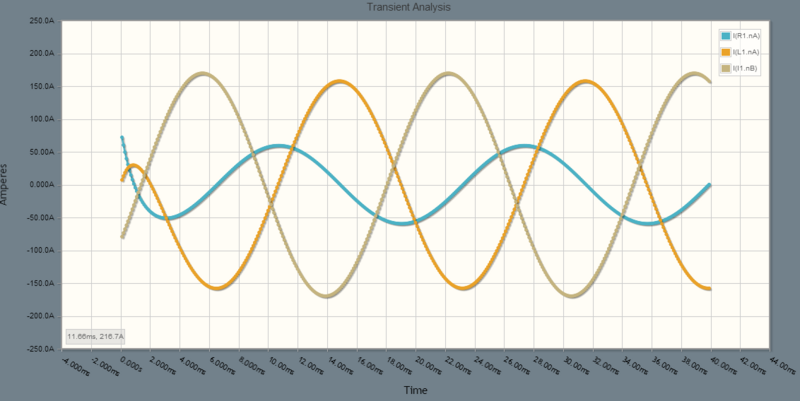
$I_{s}$（棕色）、$i_{R}$（藍色，與源電壓同相）、以及 $i_{L}$（橙色）。$i_{R}V_{s}$（藍色）超前於 $i_{L}$（橙色）${\frac {\pi }{2}}$。棕色電流（起點）在 2.09 弧度處為起點。藍色電流應該比棕色電流超前 3.30-2.09=1.21 弧度，即 69.3 度，大約為 3.21 毫秒，或比棕色電流高出 1.5 個方格。在模擬軟體處理初始能量失衡的開始階段看不到這一點，但在模擬中期，藍色電流比棕色電流超前約 1.5 個方格。所以一切正常。

功率分析

常數將為這種分析增加一些直流功率或有功功率。在不知道它們是什麼的情況下，我們無法計算出它們的影響。因此，現在我們堅持使用相量域功率分析。

$\mathbb {I} _{s}=120{\sqrt {2}}\angle 2.09$

$\mathbb {V} _{s}=599\angle 3.30$

$\mathbb {I} _{s}^{*}=120{\sqrt {2}}\angle -2.09$

如果 :$\mathbb {V} =M_{v}\angle \phi _{v}\quad$, 以及 $\quad \mathbb {I} =M_{i}\angle \phi _{i}$ 那麼

$\mathbb {S} =\mathbb {V} \mathbb {I} ^{*}={\frac {M_{v}M_{i}}{2}}\angle (\phi _{v}-\phi _{i})={\frac {120{\sqrt {2}}*599}{2}}\angle (3.30-2.09)=10,164\angle 1.21=3,586+9,510j$

以及

$cos(1.21)=.357$

這是一個糟糕的功率因數。低於 0.9 的功率因數會導致您收到電力公司的訪問，或者電線杆上的變壓器可能會炸燬。公用事業的視在功率遠大於客戶願意支付的功率。

值	單位	描述
$10,164$	伏安 va	視在功率，電力公司管理的功率：他們設計的峰值功率，他們必須提供的峰值功率
$.357$	無量綱	功率因數，有功功率與視在功率的比值，理想值為 1
$3,590$	瓦特 W	有功功率、平均功率、有效功率...消費者願意支付的功率（瓦特小時）
$9,510$	無功功率 var	無功功率...為什麼房間裡的不是所有插座都在同一個斷路器上

直覺

應該有一個方法可以在 mupad 中以符號形式進行相量數學...可能使用矩陣。