控制系統/MATLAB

MATLAB

此頁面假設您事先了解 MATLAB 的基礎知識。有關 MATLAB 的更多資訊，請參閱 MATLAB 程式設計.

MATLAB 是一種專門為矩陣操作而設計的程式語言。由於其強大的計算能力，MATLAB 是許多控制工程師設計和模擬控制系統的首選工具。本頁將討論使用 MATLAB 進行控制系統設計和分析。MATLAB 有許多名為“工具箱”的外掛模組。下面描述的幾乎所有函式都位於 控制系統工具箱 中。如果您的系統安裝了控制系統工具箱，您可以在 MATLAB 提示符下鍵入 help control 以獲取有關該工具箱的更多資訊。

此外，還有一個名為 Octave 的 MATLAB 開源競爭對手。Octave 與 MATLAB 類似，但也有一些區別。本頁將重點介紹 MATLAB，但可以新增另一頁來重點介紹 Octave。截至 2006 年 9 月 10 日，下面列出的所有 MATLAB 命令都已在 GNU octave 中實現。

本頁將使用 {{MATLAB CMD}} 模板來顯示可用於執行不同任務的 MATLAB 函式。

MATLAB 是 The Mathworks 生產的版權產品。有關 MATLAB 和 The Mathworks 的更多資訊，請參閱 控制系統/資源.

輸入-輸出隔離

在 MIMO 系統中，通常隔離單個輸入-輸出對以進行分析非常重要。每個輸入對應於 B 矩陣中的一行，每個輸出對應於 C 矩陣中的一列。例如，要隔離第二個輸入和第三個輸出，我們可以建立一個系統

sys = ss(A, B(:,2), C(3,:), D);

本頁將把這種技術稱為“輸入-輸出隔離”。

階躍響應

此操作可以使用此 MATLAB 命令執行

step

首先，讓我們看一下經典方法，使用以下系統

$G(s)={\frac {5s+10}{s^{2}+4s+5}}$

此係統實際上可以建模為兩個係數向量 NUM 和 DEN

NUM = [5, 10]
DEN = [1, 4, 5]

現在，我們可以使用 MATLAB step 命令來生成此係統的階躍響應

step(NUM, DEN, t);

其中 t 是一個時間向量。如果您沒有在左側提供結果，階躍函式將自動生成階躍響應的圖形圖。但是，如果您使用以下格式

[y, x, t] = step(NUM, DEN, t);

那麼 MATLAB 不會自動生成圖，您將不得不自己生成一個。

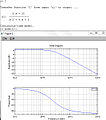
這是一個示例螢幕截圖

• 
  階躍響應

現在，讓我們看一下現代狀態空間方法。如果我們有矩陣 A、B、C 和 D，我們可以將它們代入階躍函式，如下所示

step(A, B, C, D);

或者，我們可以選擇包括時間向量 t

step(A, B, C, D, t);

同樣，如果我們在等式的左側提供結果，MATLAB 不會自動為我們生成圖。

此操作可以使用此 MATLAB 命令執行

plot

如果我們沒有得到自動生成的圖，並且我們想要生成自己的圖，我們鍵入

[y, x, t] = step(NUM, DEN, t);

然後我們可以使用 plot 命令建立圖形

plot(t, y);

y 是階躍響應的輸出幅值，而 x 是來自狀態空間方程的系統的內部狀態

$x'=Ax+Bu$

$y=Cx+Du$

經典 ↔ 現代

此操作可以使用此 MATLAB 命令執行

tf2ss

MATLAB 包含可用於從拉普拉斯表示自動轉換為狀態空間表示的功能。此函式 tf2ss 的使用方法如下

[A, B, C, D] = tf2ss(NUM, DEN);

其中 NUM 和 DEN 分別是傳遞函式的分子和分母的係數向量。

此操作可以使用此 MATLAB 命令執行

ss2tf

類似地，我們可以使用 ss2tf 函式從拉普拉斯域轉換回狀態空間表示，如下所示

[NUM, DEN] = ss2tf(A, B, C, D);

或者，如果我們有多個輸入在一個向量 u 中，我們可以將其寫成如下

[NUM, DEN] = ss2tf(A, B, C, D, u);

當我們的系統有多個輸入時，必須提供 u 引數，但如果我們只有一個輸入，則不需要提供 u 引數。這種形式的等式為每個單獨的輸入生成一個傳遞函式。NUM 和 DEN 成為二維矩陣，每行都是每個不同輸入的係數。

z 域數字濾波器

此操作可以使用此 MATLAB 命令執行

filter

現在讓我們考慮一個具有以下在 Z 域中的一般傳遞函式的數字系統

$H(z)={\frac {n(z)}{d(z)}}$

其中 n(z) 和 d(z) 分別是傳遞函式的分子和分母多項式。filter 命令可用於將輸入向量 x 應用於濾波器。輸出 y 可以從以下程式碼獲得

y = filter(n, d, x);

在這個例子中，單詞“filter”可能有點用詞不當，但事實仍然是，這是將輸入應用於數字系統的​​方法。獲得輸出幅值向量後，我們可以使用 plot 命令繪製它

plot(y);

此操作可以使用此 MATLAB 命令執行

ones

要獲得數字系統的階躍響應，我們必須首先使用 ones 命令建立一個階躍函式

u = ones(1, N);

其中 N 是我們想要在數字系統中取樣的樣本數量（不要與“n”混淆，我們的分子係數）。生成單位階躍函式後，我們可以將此函式透過數字濾波器傳遞，如下所示

y = filter(n, d, u);

我們可以繪製 y

plot(y);

狀態空間數字濾波器

同樣，我們也可以分析狀態空間表示中的數字系統。如果我們有以下數字狀態關係

$x[k+1]=Ax[k]+Bu[k]$

$y[k]=Cx[k]+Du[k]$

我們可以使用上面用過的 ss2tf 函式自動轉換為脈衝響應。

[NUM, DEN] = ss2tf(A, B, C, D);

然後，我們可以使用準備好的單位階躍序列向量 u 對其進行濾波。

y = filter(num, den, u)

這將給出我們狀態空間表示的數字系統的階躍響應。

根軌跡圖

此操作可以使用此 MATLAB 命令執行

rlocus

MATLAB 提供了一個實用的自動工具，用於根據傳遞函式生成根軌跡圖：rlocus 命令。在傳遞函式域或狀態空間域中，我們有以下函式的使用方法。

rlocus(num, den);

和

rlocus(A, B, C, D);

這些函式將自動生成系統的根軌跡圖。但是，如果我們提供左邊的引數

[r, K] = rlocus(num, den);

或者

[r, K] = rlocus(A, B, C, D);

該函式不會自動生成圖形，您需要自己生成圖形。還可以提供一個可選的增益 K 引數。

rlocus(num, den, K);

或者

rlocus(A, B, C, D, K);

如果未提供 K，MATLAB 將為您提供自動增益值。

獲得 [r, K] 值後，可以繪製根軌跡。

plot(r);

rlocus 命令不能用於 MIMO 系統，因此如果您的系統是 MIMO 系統，則必須將係數矩陣分開以隔離每個單獨的輸入輸出對，並分別繪製每個對。

這是一個示例螢幕截圖

• 
  根軌跡

數字根軌跡

為數字系統建立根軌跡圖與為連續系統建立根軌跡圖完全相同。唯一的區別是結果的解釋，因為數字系統的穩定區域與連續系統的穩定區域不同。可以使用相同的 rlocus 函式，使用方法與上面相同。

伯德圖

此操作可以使用此 MATLAB 命令執行

bode

MATLAB 還提供了一些工具來檢查系統的頻率響應特性，既可以使用伯德圖，也可以使用奈奎斯特圖。要根據傳遞函式構建伯德圖，請使用以下命令

[mag, phase, omega] = bode(NUM, DEN, omega);

或者

[mag, phase, omega] = bode(A, B, C, D, u, omega);

其中“omega”是分析幅度和相位響應點的頻率向量。如果要將幅度資料轉換為分貝，可以使用以下轉換

magdb = 20 * log10(mag);

現在應該足夠了解這種轉換，無需解釋。

此操作可以使用此 MATLAB 命令執行

logspace

當討論以分貝為單位的伯德圖時，使用對數頻率尺度是最有意義的（也是最常見的）。要建立 omega 中的對數序列，請使用 logspace 命令，如下所示

omega = logspace(a, b, n);

此命令生成 n 個點，從 $10^{a}$ 到 $10^{b}$ 對數間隔。

如果在沒有左手引數的情況下使用 bode 命令，MATLAB 將自動生成伯德相位和幅度圖的圖形。

bode 命令如果與 MIMO 系統一起使用，將使用子圖在單個繪圖視窗中生成所有輸入輸出關係圖。對於具有多個輸入和多個輸出的系統，這可能難以看清。在這種情況下，通常最好將係數矩陣分開以隔離每個單獨的輸入輸出對。

這是一個示例螢幕截圖

• 
  伯德圖（頻率響應）

奈奎斯特圖

此操作可以使用此 MATLAB 命令執行

nyquist

除了伯德圖外，我們還可以使用 nyquist 命令建立奈奎斯特圖。nyquist 命令的操作方式類似於 bode 命令（以及我們迄今為止使用過的其他命令）

[real, imag, omega] = nyquist(NUM, DEN, omega);

或者

[real, imag, omega] = nyquist(A, B, C, D, u, omega);

這裡，“real”和“imag”是包含奈奎斯特圖每個點的實部和虛部的向量。如果我們不提供右手引數，nyquist 命令會自動為我們生成奈奎斯特圖。

與 bode 命令一樣，nyquist 命令將使用子圖在一個繪圖視窗中顯示 MIMO 系統的輸入輸出關係。如果有多個輸入輸出對，可能難以看到各個圖形。

這是一個示例螢幕截圖

• 
  奈奎斯特圖

可控性

可以使用 ctrb 命令構造可控性矩陣。可以使用 gram 命令構造可控性格拉姆矩陣。

可觀測性

可以使用 obsv 命令構造可觀測性矩陣。

經驗格拉姆矩陣

可以為線性控制系統和非線性控制系統計算經驗格拉姆矩陣。經驗格拉姆矩陣框架 emgr 允許計算可控性、可觀測性和交叉格拉姆矩陣；它與 MATLAB 和 OCTAVE 相容，並且不需要控制系統工具箱。

進一步閱讀

• Ogata, Katsuhiko，“用 MATLAB 解決控制工程問題”，Prentice Hall，新澤西州，1994 年。 ISBN 0130459070
• MATLAB 程式設計.
• http://octave.sourceforge.net/
• ControlTheoryPro.com 上的 MATLAB 類別
• 經驗格拉姆矩陣框架

控制系統