資料結構/簡介

資料結構
簡介 - 漸進符號 - 陣列 - 列表結構和迭代器
 棧和佇列 - 樹 - 最小堆和最大堆 - 圖
 雜湊表 - 集合 - 權衡

計算機可以儲存和處理大量資料。正式的資料結構使程式設計師能夠將大量資料在概念上組織成易於管理的關係。

有時我們使用資料結構來讓我們做更多的事情：例如，實現資料的快速搜尋或排序。其他時候，我們使用資料結構以便我們能做更少的事情：例如，棧的概念是更一般的資料結構的有限形式。這些限制為我們提供了保證，使我們能夠更容易地推斷程式。資料結構還提供有關演算法複雜度的保證——為一項工作選擇適當的資料結構對於編寫良好的軟體至關重要。

由於資料結構是更高層次的抽象，它們向我們展示了對資料組的操作，例如將專案新增到列表中，或在佇列中查詢最高優先順序的專案。當資料結構提供操作時，我們可以將資料結構稱為抽象資料型別（有時縮寫為 ADT）。抽象資料型別可以最小化程式碼中的依賴關係，這在需要更改程式碼時很重要。由於您從較低級別的細節中抽象出來，因此一個數據結構與另一個數據結構共享的一些更高級別的共同點可以用來用另一個數據結構替換一個數據結構。

我們的程式語言配備了一組內建型別，例如整數和浮點數，這些型別允許我們使用機器處理器具有原生支援的資料物件。這些內建型別是處理器實際提供的抽象，因為內建型別隱藏了有關其執行和限制的詳細資訊。

例如，當我們使用浮點數時，我們主要關心它的值以及可以對其應用的操作。考慮計算斜邊的長度

  let c := sqrt(a * a + b * b)

從上面生成的機器程式碼將使用常見的模式來計算這些值並累積結果。事實上，這些模式是如此重複，以至於建立了高階語言來避免這種冗餘，並允許程式設計師思考計算的什麼值而不是如何計算它。

這裡有兩個有用的相關概念

封裝是指將常見模式分組到一個名稱下，然後對其進行引數化，以實現對該模式的更高層次的理解。例如，乘法運算需要兩個源值並將這兩個值的積寫入給定的目標。該操作由源和單個目標引數化。
抽象是一種將抽象的實現細節隱藏在抽象使用者之外的機制。例如，當我們相乘數字時，我們不需要知道處理器實際使用的技術，我們只需要知道它的屬性。

程式語言既是機器的抽象，也是封裝機器內部細節的工具。例如，當程式語言充分封裝使用者以使其遠離任何一臺機器時，用程式語言編寫的程式可以編譯到幾種不同的機器架構中。

在這本書中，我們對程式語言提供的抽象和封裝進行了更進一步的步驟：當應用程式變得更加複雜時，程式語言的抽象變得過於低階而無法有效地管理。因此，我們在這些較低級別結構之上構建我們自己的抽象。我們甚至可以在這些抽象之上構建進一步的抽象。每次向上構建時，我們都會失去對較低級別實現細節的訪問許可權。雖然失去這種訪問許可權聽起來像是一筆糟糕的交易，但它實際上是一筆非常划算的交易：我們主要關心的是解決手頭的難題，而不是任何瑣碎的決定，這些決定本來可以隨意地用另一個決定代替。當我們能夠在更高層次上思考時，我們就能免除這些負擔。

我們在這本書中介紹的每個資料結構都可以被認為是一個單獨的單元，它具有一組值和一組可以用來訪問或更改這些值的操作。資料結構本身可以理解為資料結構的操作集以及每個操作的屬性（即操作的作用以及我們預計需要多長時間）。

大O符號是一種常見的表達計算機程式碼效能的方式。該符號在記憶體中專案的數量和函式的平均效能之間建立了關係。對於一組 $n$ 個專案， $O(n)$ 表示特定函式平均將在該組 $n$ 個專案上執行 $n$ 次操作。 $O(1)$ 表示該函式始終執行恆定數量的操作，無論專案的數量如何。該符號僅表示演算法複雜度，因此函式可能執行更多操作，但根據慣例， $n$ 的恆定倍數將被刪除。

節點

我們首先檢視的是節點結構。節點只是一個值容器，加上指向“下一個”節點的指標（該指標可能是null）。

以上是對結構的抽象

在某些語言中，結構被稱為記錄或類。某些其他語言不直接支援結構，而是允許使用其他結構（例如元組或列表）來構建它們。

這裡，我們只關心節點包含某種形式的值，因此我們簡單地說它的型別是“元素”，因為型別並不重要。在某些程式語言中，永遠不需要指定型別（如動態型別語言，如 Scheme、Smalltalk 或 Python）。在其他語言中，型別可能需要限制為整數或字串（如靜態型別語言，如 C）。在其他語言中，包含元素型別的決定可以延遲到實際使用型別時（如支援泛型型別的語言，如 C++ 和 Java）。在任何這些情況下，將虛擬碼翻譯成您自己的語言都應該比較簡單。

每個指定的節點操作都可以很容易地實現

// Create a new node, with v as its contained value and next as
// the value of the next pointer
function make-node(v, node next): node
  let result := new node {v, next}
  return result
end

// Returns the value contained in node n
function get-value(node n): element
  return n.value
end

// Returns the value of node n's next pointer
function get-next(node n): node
  return n.next
end

// Sets the contained value of n to be v
function set-value(node n, v)
  n.value := v
end

// Sets the value of node n's next pointer to be new-next
function set-next(node n, new-next)
  n.next := new-next
  return new-next
end

原則上，我們更關心操作和實現策略，而不是結構本身和低級別實現。例如，我們更關心指定的時間要求，該要求指出所有操作花費的時間是 $O(1)$ 。上面的實現滿足了這個標準，因為每個操作所需的時間是恆定的。另一種看待恆定時間操作的方式是將它們視為其分析不依賴於任何變數的操作。（符號 $O(1)$ 在下一章中進行了數學定義。現在，我們可以假設它只意味著恆定時間。）

由於節點只是一個值容器和指向另一個節點的指標的容器，因此節點資料結構本身（及其實現）是多麼微不足道就不足為奇了。

從節點構建鏈

儘管節點結構很簡單，但它實際上允許我們計算僅使用固定大小整數無法計算的東西。

但首先，我們將看一下不需要使用節點的程式。以下程式將從輸入流（可以來自使用者或檔案）中讀取一系列數字，直到遇到檔案末尾，然後輸出最大數字以及所有數字的平均值。

program(input-stream in, output-stream out)
  let total := 0
  let count := 0
  let largest :=  $-\infty$ 
  
  while has-next-integer(in):
    let i := read-integer(in)
    total := total + i
    count := count + 1
    largest := max(largest, i)
  repeat
   
  println out "Maximum: " largest
  
  if count != 0:
    println out "Average: " (total / count)
  fi
end

但現在考慮解決一個類似的任務：讀取一系列數字，直到遇到檔案末尾，然後輸出最大數字以及所有能被最大數字整除的數字的平均值。這個問題不同，因為最大數字可能是最後輸入的數字：如果要計算所有能被該數字整除的數字的平均值，則需要以某種方式記住它們。可以使用變數來記住之前的數字，但變數只能在輸入的數字不多時幫助我們解決問題。

例如，假設我們給自己分配 200 個變數來儲存使用者輸入的狀態。再假設每個變數都有 64 位。即使我們對程式非常巧妙，它也只能計算 $2^{64\cdot 200}$ 種不同型別的輸入的結果。雖然這是一個非常大的組合數，但一個包含 300 個 64 位數字的列表需要更多的組合才能被正確編碼。（通常，這個問題被認為需要線性空間。所有隻需要有限個變數的程式可以在常數空間內解決。）

與其內建限制（例如，只有常數個變數）來使編碼複雜化，我們可以利用節點抽象的特性來允許我們記住計算機可以容納的任意多個數字。

program(input-stream in, output-stream out)
  let largest :=  $-\infty$ 
  let nodes := null
  
  while has-next-integer(in):
    let i := read-integer(in)
    nodes := make-node(i, nodes) // contain the value i,
                                 // and remember the previous numbers too
    largest := max(largest, i)
  repeat
  println out "Maximum: " largest

  // now compute the averages of all factors of largest
  let total := 0
  let count := 0
  while nodes != null:
    let j := get-value(nodes)
    if j divides largest:
      total := total + j
      count := count + 1
    fi
    nodes := get-next(nodes)
  repeat
  if count != 0:
    println out "Average: " (total / count)
  fi
end

在上面，如果成功讀取了n個整數，將呼叫make-noden次。這將需要建立n個節點（這些節點需要足夠的空間來容納每個節點的value和next欄位，加上內部記憶體管理開銷），因此記憶體需求將按 $O(n)$ 的順序增長。類似地，我們構建這個節點鏈，然後再次遍歷鏈，這將需要 $O(n)$ 步來建立鏈，然後還需要 $O(n)$ 步來遍歷它。

注意，當我們遍歷鏈中的數字時，實際上是按相反的順序檢視它們。例如，假設輸入到我們程式中的數字是 4、7、6、30 和 15。在遇到 EOF 後，nodes 鏈將如下所示：

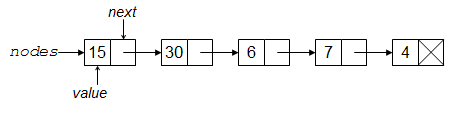
這種鏈通常被稱為連結串列。但是，我們通常更喜歡考慮列表或序列，它們不是那麼低階：連結的概念只是一個實現細節。雖然可以使用鏈來建立列表，但在本書中，我們將介紹其他幾種建立列表的方法。目前，我們更關心節點的抽象能力，而不是它使用的一種方式。

上面的演算法只使用了 make-node、get-value 和 get-next 函式。如果我們使用 set-next，我們可以改變演算法以生成鏈，使其保持原始順序（而不是反轉它）。

要執行
用於執行此操作的虛擬碼；另外，TODO；可能應該考慮使用 set-value 的引人注目但不過於高階的應用。

program (input-stream in, output-stream out)
  let largest :=  $-\infty$ 
  let nodes := null
  let tail_node := null
  
  while has-next-integer (in):
    let i := read-integer (in)
    if (nodes == null)
      nodes := make-node(i, null) // construct first node in the list
      tail_node := nodes //there is one node in the list=> first and last are the same
    else
      tail_node := set-next (tail_node, make-node (i, null)) // append new node to the end of the list
    largest := max(largest, i)
  repeat
  println out "Maximum: " largest

  // now compute the averages of all factors of largest
  let total := 0
  let count := 0
  while nodes != null:
    let j := get-value(nodes)
    if j divides largest:
      total := total + j
      count := count + 1
    fi
    nodes := get-next(nodes)
  repeat
  if count != 0:
    println out "Average: " (total / count)
  fi
end

歸納原理

我們可以從節點構建的鏈是數學歸納原理的證明。

數學歸納法

假設你有一些關於數字 $P(n)$ 的性質。
如果你能證明當 $P(n)$ 成立時， $P(n+1)$ 也必須成立，那麼
你只需要證明 $P(1)$ 成立，就可以證明對於所有自然數 $n$ ， $P(n)$ 成立。

例如，令性質 $P(n)$ 為語句“你可以建立一個容納 $n$ 個數字的鏈”。這是一個關於自然數的性質，因為這句話對於 $n$ 的特定值是有意義的。

你可以建立一個容納 5 個數字的鏈
你可以建立一個容納 100 個數字的鏈
你可以建立一個容納 1,000,000 個數字的鏈

與其證明我們可以建立長度為 5、100 和一百萬的鏈，我們更願意證明一般性語句 $P(n)$ 。上面第 2 步被稱為 **歸納假設**；讓我們證明我們可以證明它。

假設 $P(n)$ 成立。也就是說，我們可以建立一個包含 $n$ 個元素的鏈。現在我們必須證明 $P(n+1)$ 成立。
假設 chain 是 $n$ 元素鏈的第一個節點。假設 i 是我們想要新增到鏈中以建立 $n+1$ 長度鏈的某個數字。
以下程式碼可以為我們完成此操作

let bigger-chain := make-node(i, chain)

在這裡，我們有了新的數字 i，它現在是 bigger-chain 的第一個連結所包含的值。如果 chain 包含 $n$ 個元素，那麼 bigger-chain 必須包含 $n+1$ 個元素。

上面第 3 步被稱為 **基本情況**，讓我們證明我們可以證明它。

我們必須證明 $P(1)$ 成立。也就是說，我們可以建立一個包含一個元素的鏈。
以下程式碼可以為我們完成此操作

let chain := make-node(i, null)

因此，歸納原理表明，我們已經證明對於 $n$ 的所有值，我們可以建立包含 $n$ 個元素的鏈 $n\geq 1$ 。這是為什麼呢？也許理解歸納的最佳方式是，它實際上是建立公式來描述無限多個證明的方法。在我們證明了語句對於 $P(1)$ （基本情況）成立後，我們可以將歸納假設應用於該事實來證明 $P(2)$ 成立。由於我們現在知道 $P(2)$ 成立，我們可以再次應用歸納假設來證明 $P(3)$ 必須成立。該原理表明，沒有任何東西能阻止我們反覆這樣做，因此我們應該假設它在所有情況下都成立。

歸納法聽起來可能是一種奇怪的證明方法，但它是一種非常有用的技術。使這種技術如此有用的原因是，它可以將一個聽起來很困難的陳述，比如“證明 $P(n)$ 對所有 $n\geq 1$ 成立”分解成兩個更小、更容易證明的陳述。通常情況下，基本情況很容易證明，因為它們根本不是一般性陳述。大部分證明工作通常都在歸納假設中，這通常需要巧妙地重新表述陳述，以“附加”一個 $n+1$ 情況的證明。

你可以將節點的包含值視為基本情況，而將節點的下一個指標視為歸納假設。就像數學歸納法一樣，我們可以將儲存任意數量元素的難題分解成更簡單的儲存一個元素的難題，然後有一個機制來附加更多元素。

對求和的歸納法

我們接下來要考慮的歸納法的例子在本質上更多地是代數性的。

假設我們給出了公式 ${\frac {(n)(n+1)}{2}}$ ，我們想要證明這個公式給出了前 $n$ 個數字的總和。作為第一個嘗試，我們可能會嘗試僅僅證明它對 1 成立。

{\frac {(1)(1+1)}{2}}=1=1

,

對 2 成立

{\frac {(2)(2+1)}{2}}=3=1+2

,

對 3 成立

{\frac {(3)(3+1)}{2}}=6=1+2+3

等等，但是我們會很快意識到，我們所謂的證明需要無限長的時間才能寫出來！即使你完成了這個證明並證明它對前十億個數字成立，但這並不一定意味著它對十億零一或甚至一百億成立。這是一個強烈的暗示，也許歸納法在這裡會很有用。

假設我們想要證明給定的公式確實給出了前 n 個數字的總和，使用歸納法。第一步是證明基本情況；也就是說，我們必須證明它在 n = 1 時成立。這相對容易；我們只需要用 1 代替變數 n，我們得到 ( ${\frac {(1)(1+1)}{2}}=1$ )，這表明當 n = 1 時，公式是正確的。

現在進行歸納步驟。我們必須證明，如果公式對 j 成立，它對 j + 1 也成立。換句話說，假設我們已經證明了從 1 到 (j) 的總和是 ${\frac {((j))((j)+1)}{2}}$ ，我們想要證明從 1 到 (j+1) 的總和是 ${\frac {((j+1))((j+1)+1)}{2}}$ 。注意，這兩個公式只是透過分別用 (j) 和 (j+1) 替換 n 得來的。

為了證明這個歸納步驟，首先要注意，要計算從 1 到 j+1 的總和，你只需計算從 1 到 j 的總和，然後加上 j+1。我們已經有了從 1 到 j 的總和的公式，當我們把 j+1 加到那個公式中時，我們得到了這個新公式： ${\frac {((j))((j)+1)}{2}}+(j+1)$ . 所以為了真正完成證明，我們只需要證明 ${\frac {((j))((j)+1)}{2}}+(j+1)={\frac {((j+1))((j+1)+1)}{2}}$ .