資料結構/堆疊和佇列
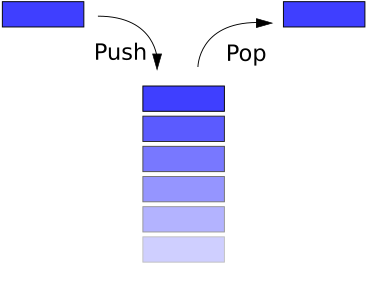
堆疊是一種基本資料結構,可以從邏輯上將其視為線性結構,用實際物理堆疊或堆來表示,在這種結構中,專案的插入和刪除發生在一個稱為堆疊頂部的末端。基本概念可以透過將您的資料集想象為一疊盤子或書籍來說明,您只能取出堆疊頂部的專案才能從中移除東西。這種結構在整個程式設計中都被使用。
堆疊的基本實現也稱為 LIFO(後進先出),以演示它訪問資料的 方式,因為正如我們將看到的那樣,堆疊實現有各種變化。
基本上可以在堆疊上執行三種操作。它們是 1)將專案插入堆疊(push)。 2)從堆疊中刪除專案(pop)。 3)顯示堆疊的內容(peek 或 top)。
下面是一些通常由堆疊資料型別支援的操作
Stack<item-type> 操作
push(new-item:item-type)- 將專案新增到堆疊。
top():item-type- 返回壓入堆疊的最後一個專案。
pop()- 從堆疊中刪除最近壓入的專案。
is-empty():Boolean- 如果不再有專案可以彈出且沒有頂部的專案,則為 true。
is-full():Boolean- 如果不再有專案可以壓入,則為 true。
get-size():Integer- 返回堆疊上的元素數量。
除了get-size()以外的所有操作都可以在時間內執行。get-size()在最壞情況下執行時間為
基本的連結串列實現是您可以執行的最簡單的堆疊實現之一。在結構上,它是一個連結串列。
type Stack<item_type>
data list:Singly Linked List<item_type>
"stack follows the LIFO (last in first out) operation"
"queue follows the FIFO (first in first out) operation"
constructor()
list := new Singly-Linked-List()
end constructor
大多數操作透過將它們傳遞到底層的連結串列來實現。當您想要將某些東西push到列表中時,您只需將其新增到連結串列的前面。然後,先前的頂部是“next”從正在新增的專案,並且列表的前面指標指向新的專案。
method push(new_item:item_type)
list.prepend(new_item)
end method
要檢視top專案,您只需檢查連結串列中的第一個專案。
method top():item_type
return list.get-begin().get-value()
end method
當您想要從列表中pop某些東西時,只需從連結串列中刪除第一個專案。
method pop()
list.remove-first()
end method
檢查是否為空很簡單。只需檢查列表是否為空。
method is-empty():Boolean
return list.is-empty()
end method
檢查是否已滿很簡單。連結串列被認為是無限大小的。
method is-full():Boolean
return False
end method
檢查大小再次傳遞到列表。
method get-size():Integer
return list.get-size()
end method
end type
釋出庫中的真實堆疊實現可能會重新實現連結串列,以便透過省略不必要的函式來從實現中擠出最後一部分效能。上面的實現為您提供了所涉及的思想,並且您可以透過內聯連結串列程式碼來完成您需要的任何最佳化。
在連結串列中,訪問第一個元素是一個操作。列表包含一個指標,用於檢查空/滿,就像這裡完成的那樣也是(取決於使用了什麼時間/空間權衡)。大多數情況下,堆疊的使用者不使用getSize()操作,因此可以透過不最佳化它來節省一些空間。
由於所有操作都在堆疊頂部,因此陣列實現現在要好得多得多。
public class StackArray implements Stack
{
protected int top;
protected Object[] data;
...
}
陣列實現將堆疊底部保留在陣列的開頭。它向陣列的末尾增長。唯一的問題是,如果您嘗試在陣列已滿時推入元素,那麼
Assert.pre(!isFull(),"Stack is not full.");
將失敗,並引發異常。因此,用 Vector(參見 StackVector)實現更有意義,以允許無界增長(以偶爾的 O(n) 延遲為代價)。
複雜度
所有操作都是 O(1),除了偶爾的 push 和 clear,它們應該用 null 替換所有條目,以便讓它們被垃圾回收。陣列實現不會替換 null 條目。Vector 實現會……

使用棧,我們可以解決許多應用,其中一些列在下面。
將十進位制數轉換為二進位制數的邏輯如下
* Read a number
* Iteration (while number is greater than zero)
1. Find out the remainder after dividing the number by 2
2. Print the remainder
3. Divide the number by 2
* End the iteration
然而,這種邏輯存在問題。假設我們要找到的二進位制形式的數字是 23。使用這種邏輯,我們得到的結果是 11101,而不是 10111。
為了解決這個問題,我們使用一個棧。我們利用棧的 *LIFO* 屬性。最初,我們將形成的二進位制數字 *push* 到棧中,而不是直接列印它。在整個數字都被轉換為二進位制形式之後,我們一次從棧中 *pop* 一個數字並列印它。因此,我們將十進位制數轉換為其正確的二進位制形式。
演算法
1. Create a stack
2. Enter a decimal number which has to be converted into its equivalent binary form.
3. iteration1 (while number > 0)
3.1 digit = number % 2
3.2 Push digit into the stack
3.3 If the stack is full
3.3.1 Print an error
3.3.2 Stop the algorithm
3.4 End the if condition
3.5 Divide the number by 2
4. End iteration1
5. iteration2 (while stack is not empty)
5.1 Pop digit from the stack
5.2 Print the digit
6. End iteration2
7. STOP

棧最有趣的應用之一是在解決一個叫做漢諾塔的謎題中。根據一個古老的婆羅門故事,宇宙的存在是根據一群僧侶所花費的時間來計算的,這些僧侶一直在工作,將 64 個圓盤從一根柱子移到另一根柱子上。但是,有一些關於如何做到這一點的規則,即
- 你一次只能移動一個圓盤。
- 為了臨時儲存,可以使用第三根柱子。
- 你不能把一個直徑較大的圓盤放在一個直徑較小的圓盤上。[1]
這裡我們假設 A 是第一根柱子,B 是第二根柱子,C 是第三根柱子。





輸出:(當有 3 個圓盤時)
假設 *1* 是最小的圓盤,*2* 是中等大小的圓盤,*3* 是最大的圓盤。
| 移動圓盤 | 從樁 | 到樁 |
|---|---|---|
| 1 | A | C |
| 2 | A | B |
| 1 | C | B |
| 3 | A | C |
| 1 | B | A |
| 2 | B | C |
| 1 | A | C |
輸出:(當有 4 個圓盤時)
| 移動圓盤 | 從樁 | 到樁 |
|---|---|---|
| 1 | A | B |
| 2 | A | C |
| 1 | B | C |
| 3 | A | B |
| 1 | C | A |
| 2 | C | B |
| 1 | A | B |
| 4 | A | C |
| 1 | B | C |
| 2 | B | A |
| 1 | C | A |
| 3 | B | C |
| 1 | A | B |
| 2 | A | C |
| 1 | B | C |
這個解決方案的 C++ 程式碼可以用兩種方法實現
這裡我們假設 A 是第一根柱子,B 是第二根柱子,C 是第三根柱子。(B 是中間的)
void TowersofHanoi(int n, int a, int b, int c)
{
//Move top n disks from tower a to tower b, use tower c for intermediate storage.
if(n > 0)
{
TowersofHanoi(n-1, a, c, b); //recursion
cout << " Move top disk from tower " << a << " to tower " << b << endl ;
//Move n-1 disks from intermediate(b) to the source(a) back
TowersofHanoi(n-1, c, b, a); //recursion
}
}
// Global variable, tower [1:3] are three towers
arrayStack<int> tower[4];
void TowerofHanoi(int n)
{
// Preprocessor for moveAndShow.
for (int d = n; d > 0; d--) //initialize
tower[1].push(d); //add disk d to tower 1
moveAndShow(n, 1, 2, 3); /*move n disks from tower 1 to tower 3 using
tower 2 as intermediate tower*/
}
void moveAndShow(int n, int a, int b, int c)
{
// Move the top n disks from tower a to tower b showing states.
// Use tower c for intermediate storage.
if(n > 0)
{
moveAndShow(n-1, a, c, b); //recursion
int d = tower[a].top(); //move a disc from top of tower a to top of
tower[a].pop(); //tower b
tower[b].push(d);
showState(); //show state of 3 towers
moveAndShow(n-1, c, b, a); //recursion
}
}
然而,上面實現的複雜度是 O()。因此,很明顯,這個問題只能解決 n 的較小值(通常 n <= 30)。在僧侶的情況下,按照上述規則將 64 個圓盤轉移所需的轉數為 18,446,744,073,709,551,615;這肯定需要很多時間!!
使用 逆波蘭表示法 的計算器使用棧結構來儲存值。表示式可以表示為字首、字尾或中綴表示法。從一種形式的表示式轉換為另一種形式可以使用棧來完成。許多編譯器使用棧來解析表示式、程式塊等的語法,然後再翻譯成低階程式碼。大多數程式語言都是 上下文無關語言,使它們能夠使用基於棧的機器進行解析。
輸入 (((2 * 5) - (1 * 2)) / (9 - 7))
輸出 4
分析:五種型別的輸入字元
* Opening bracket * Numbers * Operators * Closing bracket * New line character
資料結構要求:一個字元棧
演算法
1. Read one input character
2. Actions at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Push into stack and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop it from character stack
(2.4.1) if it is opening bracket, then discard it, Go to step (1)
(2.4.2) Pop is used three times
The first popped element is assigned to op2
The second popped element is assigned to op
The third popped element is assigned to op1
Evaluate op1 op op2
Convert the result into character and
push into the stack
Go to step (2.4)
New line character (2.5) Pop from stack and print the answer
STOP
結果:完全括號的中綴表示式的求值將以如下方式列印在顯示器上
輸入字串 (((2 * 5) - (1 * 2)) / (9 - 7))
| 輸入符號 | 棧(從底部到頂部) | 操作 |
|---|---|---|
| ( | ( | |
| ( | ( ( | |
| ( | ( ( ( | |
| 2 | ( ( ( 2 | |
| * | ( ( ( 2 * | |
| 5 | ( ( ( 2 * 5 | |
| ) | ( ( 10 | 2 * 5 = 10 & *Push* |
| - | ( ( 10 - | |
| ( | ( ( 10 - ( | |
| 1 | ( ( 10 - ( 1 | |
| * | ( ( 10 - ( 1 * | |
| 2 | ( ( 10 - ( 1 * 2 | |
| ) | ( ( 10 - 2 | 1 * 2 = 2 & *Push* |
| ) | ( 8 | 10 - 2 = 8 & *Push* |
| / | ( 8 / | |
| ( | ( 8 / ( | |
| 9 | ( 8 / ( 9 | |
| - | ( 8 / ( 9 - | |
| 9 | ( 8 / ( 9 - 7 | |
| ) | ( 8 / 2 | 9 - 7 = 2 & *Push* |
| ) | 4 | 8 / 2 = 4 & *Push* |
| 換行 | 空 | *Pop* & 列印 |
C 程式
int main (int argc, char
struct ch *charactop;
struct integer *integertop;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
while(1)
{
rd = argv[1][i++];
switch(rd)
{
case '+':
case '-':
case '/':
case '*':
case '(': charactop = cpush(charactop, rd);
break;
case ')': integertop = ipop (integertop, &op2);
integertop = ipop (integertop, &op1);
charactop = cpop (charactop, &op);
while(op != '(')
{
integertop = ipush (integertop, eval(op, op1, op2));
charactop = cpop (charactop, &op);
if (op != '(')
{
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
}
}
break;
case '\0': while (! cemptystack(charactop))
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2));
}
integertop = ipop(integertop, &op1);
printf("\n The final solution is: %d\n", op1);
return 0;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
程式的輸出
在命令列輸入的輸入:(((2 * 5) - (1 * 2)) / (9 - 7)) [3]
輸入 (2 * 5 - 1 * 2) / (11 - 9)
輸出 4
分析:有五種型別的輸入字元,即
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)
如果將運算子作為輸入字元讀取,我們不知道該怎麼辦。透過實現運算子的優先順序規則,我們找到了解決這個問題的方法。
如果讀取運算子,則應執行比較優先順序檢查,然後將其壓入。如果棧 *top* 包含的運算子的優先順序高於或等於輸入運算子的優先順序,則我們將其 *pop* 並列印它。我們不斷執行優先順序檢查,直到棧的 *top* 出現優先順序較低的運算子或不包含運算子為止。
此問題的所需資料結構:一個字元棧和一個整數棧
演算法
1. Read an input character
2. Actions that will be performed at the end of each input
Opening brackets (2.1) Push it into stack and then Go to step (1)
Digit (2.2) Push into stack, Go to step (1)
Operator (2.3) Do the comparative priority check
(2.3.1) if the character stack's top contains an operator with equal
or higher priority, then pop it into op
Pop a number from integer stack into op2
Pop another number from integer stack into op1
Calculate op1 op op2 and push the result into the integer
stack
Closing brackets (2.4) Pop from the character stack
(2.4.1) if it is an opening bracket, then discard it and Go to
step (1)
(2.4.2) To op, assign the popped element
Pop a number from integer stack and assign it op2
Pop another number from integer stack and assign it
to op1
Calculate op1 op op2 and push the result into the integer
stack
Convert into character and push into stack
Go to the step (2.4)
New line character (2.5) Print the result after popping from the stack
STOP
結果:未完全括號的中綴表示式的求值將按如下方式列印
輸入字串 (2 * 5 - 1 * 2) / (11 - 9)
| 輸入符號 | 字元棧(從底部到頂部) | 整數棧(從底部到頂部) | 執行的操作 |
|---|---|---|---|
| ( | ( | ||
| 2 | ( | 2 | |
| * | ( * | *Push* 因為 * 的優先順序更高 | |
| 5 | ( * | 2 5 | |
| - | ( * | 由於 - 的優先順序較低,我們執行 2 * 5 = 10 | |
| ( - | 10 | 我們將 10 壓入,然後壓入 - | |
| 1 | ( - | 10 1 | |
| * | ( - * | 10 1 | Push * 因為它的優先順序更高 |
| 2 | ( - * | 10 1 2 | |
| ) | ( - | 10 2 | 執行 1 * 2 = 2 並壓入 |
| ( | 8 | Pop - 並且 10 - 2 = 8 並壓入,Pop ( | |
| / | / | 8 | |
| ( | / ( | 8 | |
| 11 | / ( | 8 11 | |
| - | / ( - | 8 11 | |
| 9 | / ( - | 8 11 9 | |
| ) | / | 8 2 | 執行 11 - 9 = 2 並壓入 |
| 換行 | 4 | 執行 8 / 2 = 4 並壓入 | |
| 4 | 列印輸出,即 4 |
C 程式
int main (int argc, char *argv[])
{
struct ch *charactop;
struct integer *integertop;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
while(1)
{
rd = argv[1][i++];
switch(rd)
{
case '+':
case '-':
case '/':
case '*': while ((charactop->data != '(') && (!cemptystack(charactop)))
{
if(priority(rd) > (priority(charactop->data))
break;
else
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2);
}
}
charactop = cpush(charactop, rd);
break;
case '(': charactop = cpush(charactop, rd);
break;
case ')': integertop = ipop (integertop, &op2);
integertop = ipop (integertop, &op1);
charactop = cpop (charactop, &op);
while(op != '(')
{
integertop = ipush (integertop, eval(op, op1, op2);
charactop = cpop (charactop, &op);
if (op != '(')
{
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
}
}
break;
case '\0': while (!= cemptystack(charactop))
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2);
}
integertop = ipop(integertop, &op1);
printf("\n The final solution is: %d", op1);
return 0;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
int priority (char op)
{
switch(op)
{
case '^':
case '$': return 3;
case '*':
case '/': return 2;
case '+':
case '-': return 1;
}
}
程式的輸出
在命令列輸入的輸入 (2 * 5 - 1 * 2) / (11 - 9)
輸出: 4 [3]
輸入: x + 6 * ( y + z ) ^ 3
輸出:' 4
分析:有三種類型的輸入字元
* Numbers
* Operators
* New line character (\n)
資料結構要求:一個字元棧和一個整數棧
演算法
1. Read one character input at a time and keep pushing it into the character stack until the new
line character is reached
2. Perform pop from the character stack. If the stack is empty, go to step (3)
Number (2.1) Push in to the integer stack and then go to step (1)
Operator (2.2) Assign the operator to op
Pop a number from integer stack and assign it to op1
Pop another number from integer stack
and assign it to op2
Calculate op1 op op2 and push the output into the integer
stack. Go to step (2)
3. Pop the result from the integer stack and display the result
結果:字首表示式的求值將按如下方式列印
輸入字串 / - * 2 5 * 1 2 - 11 9
| 輸入符號 | 字元棧(從底部到頂部) | 整數棧(從底部到頂部) | 執行的操作 |
|---|---|---|---|
| / | / | ||
| - | / | ||
| * | / - * | ||
| 2 | / - * 2 | ||
| 5 | / - * 2 5 | ||
| * | / - * 2 5 * | ||
| 1 | / - * 2 5 * 1 | ||
| 2 | / - * 2 5 * 1 2 | ||
| - | / - * 2 5 * 1 2 - | ||
| 11 | / - * 2 5 * 1 2 - 11 | ||
| 9 | / - * 2 5 * 1 2 - 11 9 | ||
| \n | / - * 2 5 * 1 2 - 11 | 9 | |
| / - * 2 5 * 1 2 - | 9 11 | ||
| / - * 2 5 * 1 2 | 2 | 11 - 9 = 2 | |
| / - * 2 5 * 1 | 2 2 | ||
| / - * 2 5 * | 2 2 1 | ||
| / - * 2 5 | 2 2 | 1 * 2 = 2 | |
| / - * 2 | 2 2 5 | ||
| / - * | 2 2 5 2 | ||
| / - | 2 2 10 | 5 * 2 = 10 | |
| / | 2 8 | 10 - 2 = 8 | |
| 棧為空 | 4 | 8 / 2 = 4 | |
| 棧為空 | 列印 4 |
C 程式
int main (int argc, char *argv[])
{
struct ch *charactop = NULL;
struct integer *integertop = NULL;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
rd = argv[1][i];
while(rd != '\0')
{
charactop = cpush(charactop, rd);
rd = argv[1][i++];
}
while(!emptystack(charactop))
{
charactop = cpop(charactop, rd);
switch(rd)
{
case '+':
case '-':
case '/':
case '*':
op = rd;
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2));
break;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
int priority (char op)
{
switch(op)
{
case '^':
case '$': return 3;
case '*':
case '/': return 2;
case '+':
case '-': return 1;
}
}
程式的輸出
在命令列輸入的輸入:/ - * 2 5 * 1 2 - 11 9
輸出:4 [3]
輸入 (((8 + 1) - (7 - 4)) / (11 - 9))
輸出 8 1 + 7 4 - - 11 9 - /
分析:有五種型別的輸入字元,即
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)
需求:一個字元棧
演算法
1. Read an character input
2. Actions to be performed at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Print and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop it from the stack
(2.4.1) If it is an operator, print it, Go to step (1)
(2.4.2) If the popped element is an opening bracket,
discard it and go to step (1)
New line character (2.5) STOP
因此,將中綴表示式轉換為字尾表示式後的最終輸出如下
| 輸入 | 操作 | 棧(操作後) | 在顯示器上輸出 |
|---|---|---|---|
| ( | (2.1) 將運算元壓入棧 | ( | |
| ( | (2.1) 將運算元壓入棧 | ( ( | |
| ( | (2.1) 將運算元壓入棧 | ( ( ( | |
| 8 | (2.2) 列印它 | 8 | |
| + | (2.3) 將運算子壓入棧 | ( ( ( + | 8 |
| 1 | (2.2) 列印它 | 8 1 | |
| ) | (2.4) 從棧中彈出:由於彈出的元素是 +,因此列印它 | ( ( ( | 8 1 + |
| (2.4) 從棧中彈出:由於彈出的元素是 (,因此我們忽略它並讀取下一個字元 | ( ( | 8 1 + | |
| - | (2.3) 將運算子壓入棧 | ( ( - | |
| ( | (2.1) 將運算元壓入棧 | ( ( - ( | |
| 7 | (2.2) 列印它 | 8 1 + 7 | |
| - | (2.3) 將運算子壓入棧 | ( ( - ( - | |
| 4 | (2.2) 列印它 | 8 1 + 7 4 | |
| ) | (2.4) 從棧中彈出:由於彈出的元素是 -,因此列印它 | ( ( - ( | 8 1 + 7 4 - |
| (2.4) 從棧中彈出:由於彈出的元素是 (,因此我們忽略它並讀取下一個字元 | ( ( - | ||
| ) | (2.4) 從棧中彈出:由於彈出的元素是 -,因此列印它 | ( ( | 8 1 + 7 4 - - |
| (2.4) 從棧中彈出:由於彈出的元素是 (,因此我們忽略它並讀取下一個字元 | ( | ||
| / | (2.3) 將運算元壓入棧 | ( / | |
| ( | (2.1) 壓入棧 | ( / ( | |
| 11 | (2.2) 列印它 | 8 1 + 7 4 - - 11 | |
| - | (2.3) 將運算元壓入棧 | ( / ( - | |
| 9 | (2.2) 列印它 | 8 1 + 7 4 - - 11 9 | |
| ) | (2.4) 從棧中彈出:由於彈出的元素是 -,因此列印它 | ( / ( | 8 1 + 7 4 - - 11 9 - |
| (2.4) 從棧中彈出:由於彈出的元素是 (,因此我們忽略它並讀取下一個字元 | ( / | ||
| ) | (2.4) 從棧中彈出:由於彈出的元素是 /,因此列印它 | ( | 8 1 + 7 4 - - 11 9 - / |
| (2.4) 從棧中彈出:由於彈出的元素是 (,因此我們忽略它並讀取下一個字元 | 棧為空 | ||
| 換行符 | (2.5) 停止 |
這是一個非常好的堆疊應用。假設一輛貨運列車有 n 節車廂,每節車廂都要在不同的車站卸貨。它們編號從 1 到 n,貨運列車按順序從 n 到 1 訪問這些車站。顯然,車廂按目的地進行標記。為了方便從列車中卸下車廂,我們必須將它們按編號升序重新排列(即從 1 到 n)。當車廂按此順序排列時,它們可以在每個車站卸下。我們在一個有 輸入軌道、輸出軌道 和 k 個位於輸入軌道和輸出軌道之間的存放軌道的調車場重新排列車廂(即 存放軌道)。
為了重新排列車廂,我們從前到後檢查輸入軌道上的車廂。如果正在檢查的車廂是輸出排列中的下一個車廂,我們將其直接移動到 輸出軌道。如果不是,我們將其移動到 存放軌道,並在需要將其放置到 輸出軌道 時將其留在那裡。存放軌道以 LIFO 的方式工作,因為車廂從頂部進入和離開這些軌道。在重新排列車廂時,只允許以下移動
- 車廂可以從輸入軌道的最前部(即右端)移動到其中一個 存放軌道 的頂部或輸出軌道的左端。
- 車廂可以從 存放軌道 的頂部移動到 輸出軌道 的左端。
該圖顯示了一個有 k = 3 個存放軌道 H1、H2 和 H3,以及 n = 9 的調車場。貨運列車的 n 節車廂從輸入軌道開始,並以從右到左 1 到 n 的順序結束於輸出軌道。車廂最初以從後到前的順序排列,依次是 5、8、1、7、4、2、9、6、3。之後,車廂會按照需要的順序重新排列。

- 考慮圖中的輸入排列,這裡我們注意到車廂 3 在最前面,所以它還不能輸出,因為它要排在車廂 1 和 2 之前。所以車廂 3 被分離並移動到存放軌道 H1。
- 下一個車廂 6 不能輸出,它被移動到存放軌道 H2。因為我們必須在車廂 6 之前輸出車廂 3,如果我們將車廂 6 移動到存放軌道 H1,這是不可能的。
- 現在很明顯,我們將車廂 9 移動到 H3。
對任何存放軌道上的車廂重新排列的要求是,車廂應該從上到下按升序排列。
- 所以現在將車廂 2 移動到存放軌道 H1,這樣就滿足了前面的說法。如果我們將車廂 2 移動到 H2 或 H3,那麼我們將沒有地方移動車廂 4、5、7 或 8。當新車廂 λ 被移動到其頂部具有最小標籤 Ψ 的存放軌道時,λ < Ψ,對未來車廂放置的限制最少。我們可能將其稱為分配規則,以決定特定車廂是否屬於特定存放軌道。
- 當考慮車廂 4 時,有三個地方可以移動車廂:H1、H2 和 H3。這些軌道的頂部分別是 2、6 和 9。所以使用前面提到的分配規則,我們將車廂 4 移動到 H2。
- 車廂 7 被移動到 H3。
- 下一個車廂 1 具有最小標籤,所以它被移動到輸出軌道。
- 現在是輸出車廂 2 和 3 的時候了,它們來自 H1(簡而言之,所有來自 H1 的車廂都附加到輸出軌道上的車廂 1)。
車廂 4 被移動到輸出軌道。現在沒有其他車廂可以移動到輸出軌道。
- 下一個車廂,車廂 8,被移動到存放軌道 H1。
- 車廂 5 從輸入軌道輸出。車廂 6 從 H2 移動到輸出軌道,車廂 7 從 H3 移動到輸出軌道,車廂 8 從 H1 移動到輸出軌道,車廂 9 從 H3 移動到輸出軌道。
排序是指將一組元素按特定順序排列。無論是升序還是降序,按基數還是字母順序,或者其他變體。最終排序的可能性只會受源元素型別的限制。
快速排序是一種 分而治之 型別的演算法。在這種方法中,要對一組數字進行排序,我們將它縮減為兩個更小的集合,然後對這些更小的集合進行排序。
以下示例可以解釋這一點
假設 A 是以下數字的列表
在縮減步驟中,我們找到一個數字的最終位置。在本例中,假設我們必須找到 48 的最終位置,它是列表中的第一個數字。
為此,我們採用以下方法。從最後一個數字開始,從右到左移動。將每個數字與 48 進行比較。如果數字小於 48,我們在該數字處停止並將其與 48 交換。
在本例中,該數字是 24。因此,我們將 24 和 48 交換。
48 右邊的數字 96 和 72 大於 48。現在從 24 開始,以相反的方向掃描數字,即從左到右。將每個數字與 48 進行比較,直到找到大於 48 的數字。
在本例中,它是 60。因此我們將 48 和 60 交換。
注意 48 左邊的數字 12、24 和 36 都小於 48。現在,從 60 開始,以從右到左的方向掃描數字。一旦找到較小的數字,就將其與 48 交換。
在本例中,它是 44。將其與 48 交換。最終結果是
現在,從 44 開始,從左到右掃描列表,直到找到大於 48 的數字。
這樣的數字是 84。將其與 48 交換。最終結果是
現在,從 84 開始,從右到左遍歷列表,直到到達小於 48 的數字。我們在到達 48 之前沒有找到這樣的數字。這意味著列表中的所有數字都已被掃描並與 48 進行比較。此外,我們注意到所有小於 48 的數字都在它左邊,所有大於 48 的數字都在它右邊。
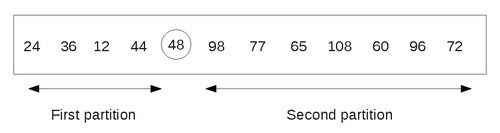
最終分割槽如下
因此,48 已被放置到正確的位置,現在我們的任務簡化為對兩個分割槽進行排序。上述建立分割槽的步驟可以對包含 2 個或更多元素的每個分割槽重複。由於我們一次只能處理一個分割槽,因此我們應該能夠跟蹤其他分割槽,以備將來處理。
這是透過使用兩個名為 LOWERBOUND 和 UPPERBOUND 的 堆疊 來完成的,以臨時儲存這些分割槽。分割槽的第一個和最後一個元素的地址分別被推入 LOWERBOUND 和 UPPERBOUND 堆疊。現在,只有在從堆疊中 彈出 其邊界值後,才將上述縮減步驟應用於分割槽。
我們可以從以下示例中理解這一點
取上述包含 12 個元素的列表 A。該演算法首先將 A 的邊界值,即 1 和 12,分別推入 LOWERBOUND 和 UPPERBOUND 堆疊。因此堆疊如下所示
LOWERBOUND: 1 UPPERBOUND: 12
為了執行縮減步驟,堆疊頂部的值從堆疊中彈出。因此,兩個堆疊都變為空。
LOWERBOUND: {empty} UPPERBOUND: {empty}
現在,縮減步驟導致 48 被固定在第 5 個位置並建立了兩個分割槽,一個是從位置 1 到 4,另一個是從位置 6 到 12。因此,值 1 和 6 被推入 LOWERBOUND 堆疊,4 和 12 被推入 UPPERBOUND 堆疊。
LOWERBOUND: 1, 6 UPPERBOUND: 4, 12
為了再次應用縮減步驟,堆疊頂部的值被彈出。因此,值 6 和 12 被彈出。因此堆疊看起來像
LOWERBOUND: 1 UPPERBOUND: 4
現在將縮減步驟應用於第二個分割槽,即從第 6 個元素到第 12 個元素。
在縮減步驟之後,98 被固定在第 11 個位置。因此,第二個分割槽只有一個元素。因此,我們將第一個分割槽的上下邊界值推入堆疊。因此,堆疊如下所示
LOWERBOUND: 1, 6 UPPERBOUND: 4, 10
處理以以下方式進行,並在堆疊不包含要處理的分割槽的任何上下邊界以及列表已排序時結束。
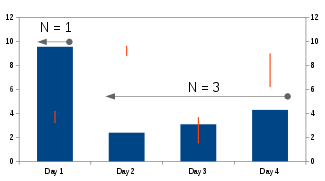
在股票跨度問題中,我們將使用堆疊來解決一個金融問題。
假設對於一隻股票,我們有一系列 n 天的每日價格報價,該股票在特定日期的價格 跨度 定義為股票價格在當前日期低於或等於該日期價格的連續天數的最大值。
輸入:一個包含 n 個元素的陣列 P
輸出:一個包含n個元素的陣列S,其中S[i]是滿足以下條件的最大整數k:k <= i + 1 且 P[j] <= P[i](j = i - k + 1,.....,i)。
演算法
1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 repeat
3.3.1 if (P[i - k] <= P[i]) then
Increment k by 1
3.3.2 else
Done with true condition
3.4 Till (k > i) or done with processing
Assign value of k to S[i] to get the span of the stock
4. Return array S
現在,分析該演算法的執行時間,我們觀察到
- 我們在開始時初始化了陣列S,並在最後返回它。這是一個常數時間操作,因此需要O(n)時間。
- repeat迴圈巢狀在for迴圈內。for迴圈的計數器為i,執行n次。不在repeat迴圈內,但在for迴圈內的語句執行了n次。因此,這些語句以及i的遞增和條件測試需要O(n)時間。
- 在外部for迴圈的i次重複中,內部repeat迴圈的主體最多執行i + 1次。在最壞情況下,元素S[i]大於所有之前的元素。因此,對if條件的測試,以及之後的語句,以及對until條件的測試,將在外部for迴圈的第i次迭代中執行i + 1次。因此,內部迴圈的總時間為O(n(n + 1)/2),即O()
所有這些步驟的執行時間透過將所有這三個步驟所花費的時間相加來計算。前兩個項是O(),而最後一項是O()。因此,該演算法的總執行時間為O()。
具有線性時間複雜度的演算法
[edit | edit source]為了更有效地計算跨度,我們注意到,如果我們知道i之前最接近的那一天,使得該天的股票價格高於當前天的股票價格,則可以輕鬆地計算出特定一天的跨度。如果存在這樣的日子,我們可以用h(i)表示它,並將h(i)初始化為-1。
因此,特定一天的跨度由公式s = i - h(i)給出。
為了實現這種邏輯,我們使用堆疊作為抽象資料型別來儲存日期i、h(i)、h(h(i))等等。當我們從第i-1天到第i天時,我們會彈出股票價格低於或等於p(i)的日期,然後將第i天的值推回到堆疊中。
這裡,我們假設堆疊由O(1)(即常數時間)的操作實現。該演算法如下所示
輸入:一個包含n個元素的陣列P和一個空的堆疊N
輸出:一個包含n個元素的陣列S,其中S[i]是滿足以下條件的最大整數k:k <= i + 1 且 P[j] <= P[i](j = i - k + 1,.....,i)。
演算法
1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 while not (Stack N is empty or done with processing)
3.3.1 if ( P[i] >= P[N.top())] then
Pop a value from stack N
3.3.2 else
Done with true condition
3.4 if Stack N is empty
3.4.1 Initialize h to -1
3.5 else
3.5.1 Initialize stack top to h
3.5.2 Put the value of h - i in S[i]
3.5.3 Push the value of i in N
4. Return array S
現在,分析該演算法的執行時間,我們觀察到
- 我們在開始時初始化了陣列S,並在最後返回它。這是一個常數時間操作,因此需要O(n)時間。
- while迴圈巢狀在for迴圈內。for迴圈的計數器為i,執行n次。不在repeat迴圈內,但在for迴圈內的語句執行了n次。因此,這些語句以及i的遞增和條件測試需要O(n)時間。
- 現在,觀察i次重複for迴圈時內部while迴圈的情況。done with a true condition語句最多執行一次,因為它會導致退出迴圈。假設t(i)是執行Pop a value from stack N語句的次數。因此,很明顯,while not (Stack N is empty or done with processing)最多測試t(i) + 1次。
- 將while迴圈中所有操作的執行時間加起來,我們得到
- 從堆疊N中彈出的元素永遠不會被推回堆疊中。因此,
因此,while迴圈中所有語句的執行時間為O()
演算法中所有步驟的執行時間透過將所有這些步驟所花費的時間相加來計算。每個步驟的執行時間為O()。因此,該演算法的執行時間複雜度為O()。
相關連結
[edit | edit source]佇列
[edit | edit source]佇列是一種基本的資料結構,在整個程式設計過程中都有使用。你可以把它想象成雜貨店的隊伍。排在隊伍最前面的人是第一個被服務的人。就像佇列一樣。
佇列也被稱為FIFO(先進先出),以演示它訪問資料的方式。
Queue<item-type>操作
enqueue(new-item:item-type)- 將一個專案新增到佇列的末尾。
front():item-type- 返回佇列最前面的專案。
dequeue()- 從佇列的前面移除專案。
is-empty():Boolean- 如果不再有專案可以出隊,並且沒有前面的專案,則為真。
is-full():Boolean- 如果不再有專案可以入隊,則為真。
get-size():Integer- 返回佇列中的元素數量。
除了get-size()以外的所有操作都可以在時間內執行。get-size()在最壞情況下執行時間為
基本的連結串列實現使用一個單向連結串列,並帶有一個尾指標來跟蹤佇列的尾部。
type Queue<item_type>
data list:Singly Linked List<item_type>
data tail:List Iterator<item_type>
constructor()
list := new Singly-Linked-List()
tail := list.get-begin() # null
end constructor
當你想入隊某個元素時,你只需將它新增到尾指標指向的元素的後面。所以,之前尾部被認為是新新增元素的下一個元素,並且尾指標指向新元素。如果列表為空,這將不起作用,因為尾部迭代器不指向任何元素。
method enqueue(new_item:item_type)
if is-empty()
list.prepend(new_item)
tail := list.get-begin()
else
list.insert_after(new_item, tail)
tail.move-next()
end if
end method
佇列上的頭部元素就是連結串列頭指標指向的那個元素。
method front():item_type
return list.get-begin().get-value()
end method
當你想出隊列表中的某個元素時,只需將頭指標指向頭部的上一個元素。舊的頭元素就是從列表中刪除的元素。如果列表現在為空,我們必須修復尾部迭代器。
method dequeue()
list.remove-first()
if is-empty()
tail := list.get-begin()
end if
end method
檢查是否為空很簡單。只需檢查列表是否為空。
method is-empty():Boolean
return list.is-empty()
end method
檢查是否已滿很簡單。連結串列被認為是無限大小的。
method is-full():Boolean
return False
end method
檢查大小再次傳遞到列表。
method get-size():Integer
return list.get-size()
end method
end type
在連結串列中,訪問第一個元素是一個 操作,因為列表包含一個直接指向它的指標。因此,入隊、頭部和出隊都是快速的 操作。
此處完成的空/滿檢查也是。
getSize()的效能取決於連結串列實現中對應操作的效能。它可能是,也可能是,這取決於所做的時間/空間權衡。大多數情況下,佇列的使用者不使用getSize()操作,因此可以透過不最佳化它來節省一些空間。
雙端佇列是一個同構元素列表,其中插入和刪除操作在兩個端點上執行。
由於這個屬性,它被稱為雙端佇列,即雙端佇列。
雙端佇列有兩種型別
- 輸入限制佇列:它只允許在一個端點插入
- 輸出限制佇列:它只允許在一個端點刪除