資料結構/樹
樹是一個非空集合,其中一個元素被指定為樹的根,而其餘元素被劃分為非空集合,每個集合都是根的子樹。
樹節點具有許多有用的屬性。節點的深度是從根節點到該節點的路徑長度(或邊數)。節點的高度是從該節點到其葉子的最長路徑。樹的高度是根節點的高度。葉子節點沒有子節點——它唯一的路徑是向上到其父節點。
有關更多資訊,請參見樹的公理化發展及其結果。
樹的型別
二叉樹:每個節點有零個、一個或兩個子節點。這個斷言使許多樹操作變得簡單和高效。
二叉搜尋樹:二叉樹,其中任何左子節點的值都小於其父節點,任何右子節點的值都大於或等於其父節點的值。
許多問題要求我們以系統的方式訪問樹的節點:例如,計算存在多少個節點或找到最大元素的任務。二叉樹可以使用三種不同的方法:先序、後序和中序,它們都做三件事:遞迴地遍歷左子樹和右子樹,並訪問當前節點。不同之處在於演算法何時訪問當前節點。
先序:當前節點,左子樹,右子樹(DLR)
後序:左子樹,右子樹,當前節點(LRD)
中序:左子樹,當前節點,右子樹(LDR)
層序:從根節點開始,逐層,從左到右。
- 訪問意味著執行一些涉及樹中當前節點的操作,例如增加計數器或檢查當前節點的值是否大於任何其他記錄的值。
preorder(node) visit(node) if node.left ≠ null then preorder(node.left) if node.right ≠ null then preorder(node.right)
inorder(node) if node.left ≠ null then inorder(node.left) visit(node) if node.right ≠ null then inorder(node.right)
postorder(node) if node.left ≠ null then postorder(node.left) if node.right ≠ null then postorder(node.right) visit(node)
levelorder(root) queue<node> q q.push(root) while not q.empty do node = q.pop visit(node) if node.left ≠ null then q.push(node.left) if node.right ≠ null then q.push(node.right)
對於對堆疊壓力較小的演算法,請參見執行緒樹。
preorder: 50,30, 20, 40, 90, 100 inorder: 20,30,40,50, 90, 100 postorder: 20,40,30,100,90,50
當已經排序的條目儲存在樹中時,所有新記錄都將走相同的路線,並且樹看起來更像一個列表(這樣的樹被稱為退化樹)。因此,樹需要平衡例程,確保所有分支下都有相同數量的記錄。這將使樹的搜尋速度保持在最佳狀態。具體來說,如果一個具有n個節點的樹是退化樹,那麼穿過樹的最長路徑將是 n 個節點;如果它是平衡樹,那麼最長路徑將是log n個節點。
演算法/左旋轉:這展示瞭如何應用平衡來在一個Treap中建立優先順序堆的不變性,Treap是一種資料結構,它具有堆的排隊效能和樹的關鍵查詢效能。平衡操作可以改變樹結構,同時保持另一個順序,即二叉樹排序順序。二叉樹順序是從左到右,左節點的鍵小於右節點的鍵,而優先順序順序是從上到下,較高節點的優先順序大於較低節點的優先順序。或者,優先順序可以被視為另一個排序鍵,只是查詢特定鍵更加複雜。
平衡操作可以移動節點上下樹,而不會影響左右順序。
AVL:根據以下規範平衡的二叉搜尋樹:任何節點的兩個子樹的高度差最多為一。
紅黑樹:一個平衡的二叉搜尋樹,使用基於分配給節點的顏色以及附近節點的顏色來進行平衡演算法。
AA 樹:一個平衡樹,實際上是紅黑樹的更嚴格變體。
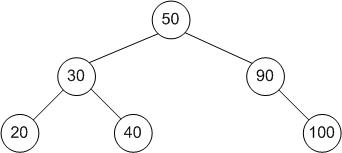
一個典型的二叉搜尋樹看起來像這樣
節點儲存在樹中的任何專案。根節點樹中的頂層專案。(樹中上面的 50)子節點當前節點下的節點。(樹中上面的 20 和 40 是 30 的子節點)父節點直接在當前節點上方的節點。(樹中上面的 90 是 100 的父節點)葉子節點沒有子節點的節點。(樹中上面的 20 是葉子節點)
要在二叉樹中搜索一個專案
- 從根節點開始
- 如果您要搜尋的專案小於根節點,則移動到根節點的左子節點;如果您要搜尋的專案大於根節點,則移動到根節點的右子節點;如果它等於根節點,那麼您已經找到了要查詢的專案。
- 現在檢查您要搜尋的專案是否等於、小於或大於您所在的新的節點。同樣,如果您要搜尋的專案小於當前節點,則移動到左子節點;如果您要搜尋的專案大於當前節點,則移動到右子節點。
- 重複此過程,直到找到要搜尋的專案,或者直到節點在正確的分支上沒有子節點,在這種情況下,樹不包含您要搜尋的專案。
例如,要查詢節點 40...
- 根節點是 50,它大於 40,因此您轉到 50 的左子節點。
- 50 的左子節點是 30,它小於 40,因此您接下來轉到 30 的右子節點。
- 30 的右子節點是 40,因此您找到了要查詢的專案 :)
.........
- 要新增一個專案,您首先必須遍歷樹,找到要放置它的位置。您遵循上述步驟進行操作。
- 當您到達一個節點,該節點在正確分支上沒有子節點時,就在那裡新增新的節點。
例如,要新增節點 25...
- 根節點是 50,它大於 25,因此您轉到 50 的左子節點。
- 50 的左子節點是 30,它大於 25,因此您轉到 30 的左子節點。
- 30 的左子節點是 20,它小於 25,因此您轉到 20 的右子節點。
- 20 的右子節點不存在,因此您在那裡新增 25 :)
假設您已經使用上面描述的搜尋技術找到了要刪除的節點。
例如,要刪除 40...
- 只需刪除節點!
- 將要刪除的節點的子節點直接連線到要刪除的節點的父節點。
例如,要刪除 90...
- 刪除 90,然後使 100 成為 50 的子節點。
一種非標準方法是將節點旋轉到選定的子樹中,並嘗試從該子樹中遞迴地再次刪除鍵,直到出現情況 1 或情況 2。這可能會使樹失去平衡,因此隨機選擇向右旋轉還是向左旋轉可能會有所幫助。
標準方法是選擇左子節點或右子節點,例如右子節點,然後透過從右子節點開始,一直向左移動,直到下一個左為 null,來獲取右節點的最左後代。然後移除右子節點的這個最左後代,用其右子樹替換它(它的左子節點為 null)。然後使用這個以前右子節點的最左後代的內容,替換要刪除的節點的鍵和值,以便其值現在位於已刪除的節點(右子節點的父節點)中。這仍然維護所有節點的鍵排序。下面是 treap 示例程式碼中的 Java 程式碼示例。
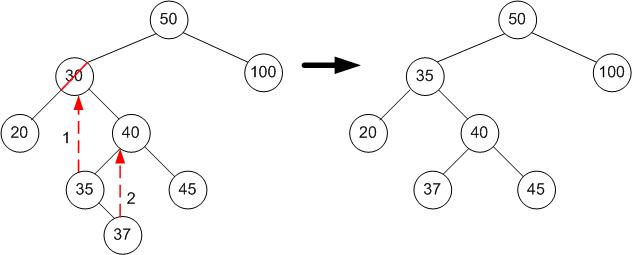
以下示例使用標準演算法,即後繼是待刪除節點的右子樹中最左邊的節點。
例如,要刪除 30
- 要刪除的節點的右節點是 40。
- (從現在開始,我們一直轉到左節點,直到沒有另一個節點......)40 的第一個左節點是 35。
- 35 沒有左節點,因此 35 是後繼者!
- 35 替換 30,位於原始右節點,具有 35 的節點被刪除,用其右子樹(根節點為 37)替換。
- 直接將待刪除節點右側的子節點移動到待刪除節點的位置。
- 由於新節點沒有左子節點,您可以將已刪除節點的左子樹的根節點作為其左子節點。
例如,要刪除 30
- 用後繼的內容(40)替換要刪除的內容(30)。
- 刪除後繼節點(內容為 40),用其右子樹(頭部內容為 45)替換它。
這最好用一個例子來說明
要刪除 30...
- 用後繼的內容(35)替換要刪除的內容(30)。
- 用其右子樹(37)替換後繼節點(35)。沒有左子樹,因為後繼節點是最左邊的。
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del);
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// non-standard method,
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
紅黑樹是一種自平衡樹結構,它為每個節點應用一種顏色。紅黑樹的結構必須遵守一組規則,這些規則規定了特定顏色節點的排列方式。當樹以某種方式修改時,就會應用這些規則,在插入新節點或刪除舊節點時,會導致某些節點的旋轉和重新著色。這使紅黑樹保持平衡,保證搜尋複雜度為 O(log n)。
紅黑樹必須遵守的規則如下:
- 每個節點必須是紅色或黑色。
- 根節點始終是黑色。
- 樹中的所有葉節點都是黑色(葉節點不包含資料,可以在大多數程式語言中建模為null 或nil 引用)。
- 每個紅色節點必須有兩個黑色子節點。
- 從給定節點到其任何後代葉節點的每條路徑必須包含相同數量的黑色節點。
紅黑樹可以建模為 2-3-4 樹,它是 B 樹(如下)的子類。帶有 1 個紅色節點的黑色節點可以看作是連結在一起的 3-節點,帶有 2 個紅色子節點的黑色節點可以看作是 4-節點。
4-節點被拆分,生成兩個節點,中間節點變為紅色,這將使中間節點的父節點(沒有紅色子節點)從 2-節點變為 3-節點,並將帶有 1 個紅色子節點的父節點變為 4-節點(但這不是總是左紅色節點)。
兩個紅色節點的內聯排列被旋轉成帶有兩個紅色子節點的父節點,即 4-節點,然後被拆分,如前所述。
A right rotate 'split 4-node' |red
red / \ --> B ---> B
B red/ \red / \
red / \ C A C A
C D / /
D D
Sedgewick 提到的最佳化是,所有插入的右紅色節點都被左旋轉,變成左紅色節點,因此只有內聯的左紅色節點需要在拆分之前右旋轉。Arne Anderson 在 1993 年的論文中描述的 AA 樹(上面)似乎是這種簡化的早期闡述,然而他建議使用右傾斜的“紅色標記”而不是左傾斜的“紅色標記”,正如 Sedgewick 建議的那樣,但 AA 樹似乎優先於左傾斜的紅黑樹。如果將來將 Linux CFS 排程程式描述為“基於 AA 的”,那將是一個相當大的衝擊。
總之,紅黑樹是一種檢測到同一個側面的兩次插入,並在情況變得更糟之前將樹拉平的方法。兩次左側插入將被旋轉,兩次右側插入在左旋轉以移除右傾斜的紅色節點後將看起來像兩次左側插入。同一父節點的兩次平衡插入可能會導致 4-節點拆分而無需旋轉,因此出現了一個問題,即紅黑樹是否可以被 a < P < b 的一側三元組的序列插入攻擊,然後是下一個三元組的 P' < a。
以下是 Python 說明程式碼
RED = 1
BLACK = 0
class Node:
def __init__(self, k, v):
# all newly inserted node's are RED
self.color = RED
self.k = k
self.v = v
self.left = None
self.right = None
class RBTree:
def __init__(self):
self.root = None
def insert(self, k, v) :
self.root = self._insert(self.root, k,v)
def _insert(self, n , k, v):
if n is None:
return Node(k,v)
if k < n.k :
n.left = self._insert(n.left, k , v)
elif k > n.k :
n.right = self._insert(n.right, k, v)
if n.right.color is RED:
#always on the left red's
#left rotate
tmp = n.right
n.right = tmp.left
tmp.left = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.left.color
n.left.color = tmpcolor
if n.left <> None and n.left.left <> None and n.left.left.color == RED and n.left.color == RED:
# right rotate in-line reds
print "right rotate"
tmp = n.left
n.left = tmp.right
tmp.right = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.right.color
n.right.color = tmpcolor
if n.left <> None: print n.left.color, n.color, n.right.color
#no need to test, because after right rotation, will need to split 3-node , as right rotation has
#brought red left grandchild to become left red child, and left red child is now red right child
#so there are two red children.
#if n.left <> None and n.right <> None and n.left.color == RED and n.right.color == RED:
print "split"
n.color = RED
n.left.color = BLACK
n.right.color = BLACK
return n
def find(self, k):
return self._find_rb(k, self.root)
def _find_rb(self, k, n):
if n is None:
return None
if k < n.k:
return self._find_rb( k, n.left)
if k > n. k:
return self._find_rb( k, n.right)
return n.v
def inorder(self):
self.inorder_visit(self.root, "O")
def inorder_visit(self, node,label=""):
if node is None: return
self.inorder_visit(node.left, label+"/L")
print label, "val=", node.v
self.inorder_visit(node.right, label+"/R")
def test1(N):
t = RBTree()
for i in xrange(0,N):
t.insert(i,i)
l = []
t.inorder()
for i in xrange(0,N):
x =t.find(i)
if x <> None:
l.append((x, i) )
print "found", len(l)
if __name__ == "__main__":
import random
test1(100000)
test1(1000)
test1(100)
test1(10)
- 二叉樹的節點有兩個子節點,左子節點及其所有後代小於節點的“值”,右子節點及其所有後代大於節點的“值”,而 B 樹是對此的概括。
- 概括是,節點不是一個值,而是一個值列表,列表的大小為 n(n > 2)。n 被選擇以最佳化儲存,以便節點的大小對應於一個塊,例如。這是在 ssd 驅動器出現之前的年代,但在 ssd ram 上搜索二叉節點仍然比搜尋 ssd ram 中的值塊,載入到普通 ram 和 cpu 快取中,然後搜尋載入的列表要慢。
- 在列表開頭,列表第一個元素的左孩子的值小於第一個元素,其所有孩子也如此。第一個元素的右邊是一個孩子,其值大於第一個元素的值,其所有孩子也如此,但也小於第二個元素的值。可以使用歸納法,對於元素 1 和 2 之間的孩子、2 和 3 之間的孩子、... 直到 n-1 和第 n 個節點,都成立。
- 在非滿 B 樹節點中插入,相當於在排序列表中插入。
- 在 B+ 樹中,插入只能在葉子節點進行,非葉子節點包含相鄰子節點之間分隔值的副本,例如元素右孩子節點列表中最左邊的值。
- 當列表變得滿時,例如有 n 個節點,節點會被“分裂”,這意味著建立兩個新的節點,並將分隔值傳遞給父節點。
B 樹最初被描述為二叉搜尋樹的泛化,其中二叉樹是 2 節點 B 樹,2 代表兩個孩子,由 2-1 = 1 個鍵分隔兩個孩子。因此,3 節點有 2 個值分隔 3 個孩子,N 節點有 N 個孩子,由 N-1 個鍵分隔。
經典的 B 樹可以有 N 節點內部節點,以及空 2 節點作為葉子節點,或者更方便地,孩子可以是值或者指向下一個 N 節點的指標,所以它是聯合。
B 樹的主要思想是,從一個根節點 N 節點開始,它可以儲存 N-1 個條目,但在第 N 個條目時,節點的鍵數用盡,節點可以分裂成兩個大小為 N/2 的 N 節點,由單個鍵 K 分隔,它等於右節點最左邊的鍵,所以任何鍵 K2 等於或大於 K 的條目都放在右節點,小於 K 的條目都放在左節點。當根節點分裂時,建立一個新的根節點,包含一個鍵,以及一個左孩子和一個右孩子。由於有 N 個孩子,但只有 N-1 個條目,所以最左邊的孩子被儲存為一個單獨的指標。如果最左邊的指標分裂,則左半部分成為新的最左邊的指標,右半部分和分隔鍵被插入到條目的前面。
另一種是 B+ 樹,它在資料庫系統中最常使用,因為只有值儲存在葉子節點中,而內部節點只儲存鍵和指向其他節點的指標,限制了資料值的大小,因為指標的大小。這通常允許具有更多條目的內部節點適合一定的塊大小,例如 4K 是常見的物理磁碟塊大小。因此,如果 B+ 樹內部節點與物理磁碟塊對齊,則從磁碟讀取大型索引塊的主要速率限制因素(因為它沒有快取在記憶體塊列表中)將減少到一次塊讀取。
B+ 樹具有更大的內部節點,因此理論上比等效的 B 樹更寬更短,後者必須將所有節點都容納在給定的物理塊大小內,因此總的來說,由於扇出更大,到達鍵的平均高度更低,因此它是更快的索引。
顯然,這種扇出非常重要,壓縮也可以應用於塊,以增加適合給定底層塊大小的條目數量(底層通常是檔案系統塊)。
大多數資料庫系統使用 B+ 樹演算法,包括 postgresql、mysql、derbydb、firebird、許多 Xbase 索引型別等。
許多檔案系統也使用 B+ 樹來管理它們的塊佈局(例如 xfs、NTFS 等)。
Transwiki 有一個 B+ 樹的 Java 實現,它使用傳統的陣列作為鍵列表和值列表。
下面是一個 B 樹的示例,帶有測試驅動程式,以及一個 B+ 樹,帶有測試驅動程式。記憶體/磁碟管理未包含在內,但在 雜湊記憶體檢查示例 中可以找到一個可用的 hack 示例。
這個 B+ 樹實現是從 B 樹中寫出來的,與 transwiki B+ 樹的不同之處在於,它試圖使用標準 Java 集合庫中已存在的 SortedMap 和 SortedSet 的語義。
因此,這個 B+ 實現的扁平葉子塊列表不能包含不包含任何資料的塊,因為排序依賴於條目的第一個鍵,所以需要建立一個包含其第一個條目的葉子塊。
一個 B 樹 Java 示例
[edit | edit source]package btreemap;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.TreeMap;
/** can't work without setting a comparator */
public class BTreeMap<K, V> implements SortedMap<K, V> {
private static final int NODE_SIZE = 100;
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return comparator;
}
Comparator< ? super K> defaultComparator = new
Comparator< K>() {
@Override
public int compare(K o1, K o2) {
// TODO Auto-generated method stub
Comparable c1 = (Comparable)o1;
Comparable c2 = (Comparable)o2;
return c1.compareTo(c2);
}
};
Comparator<? super K> comparator = defaultComparator;
BTBlock<K, V> root = new BTBlock<K, V>(NODE_SIZE, comparator);
/**
*
* @param comparator
* - this is mandatory for the tree to work
*/
public void setComparator(Comparator<? super K> comparator) {
this.comparator = comparator;
root = new BTBlock<K, V>(NODE_SIZE, comparator);
}
/**
*
*
*
* @param <K>
* @param <V>
* the entry is associated with a right child block.
*
*/
static class BlockEntry<K, V> {
K k;
V v;
BTBlock left;
BlockEntry() {
}
BlockEntry(K k, V v) {
left = null;
this.k = k;
this.v = v;
}
}
/**
*
* - this represents the result of splitting a full block into
* a left block, and a right block, and a median key, the right
* block and the median key held in a BlockEntry structure as above.
* @param <K>
* @param <V>
* @param <V>g
*/
static class SplitRootEntry<K, V> {
BTBlock<K, V> right;
BlockEntry<K, V> entry;
SplitRootEntry(BlockEntry<K, V> entry, BTBlock<K, V> right) {
this.right = right;
this.entry = entry;
}
SplitRootEntry() {
super();
}
}
/**
* this is used to return a result of a possible split , during recursive
* calling.
*
*
*
* @param <K>
* @param <V>
*/
static class resultAndSplit<K, V> {
/**
* null , if there is no split.
*/
SplitRootEntry<K, V> splitNode;
V v;
resultAndSplit(V v) {
this.v = v;
}
resultAndSplit(SplitRootEntry<K, V> entry, V v) {
this.v = v;
this.splitNode = entry;
}
}
/**
* used to represent the insertion point after searching a block if compare
* is zero, then a match was found, and pos is the insertion entry if
* compare < 0 and pos == 0 , then the search ended up less than the
* leftmost entry else compare > 0 , and the search will be to the immediate
* right of pos.
*
*
*
*/
static class PosAndCompare {
int pos = 0;
int compare = 0;
}
static class BTBlock<K, V> {
List<BlockEntry<K, V>> entries;
BTBlock<K, V> rightBlock = null;
private int maxSz = 0;
Comparator<? super K> comparator;
Comparator<? super K> comparator() {
return comparator;
}
public BTBlock(int size, Comparator<? super K> c) {
entries = new ArrayList<BlockEntry<K, V>>();
maxSz = size;
this.comparator = c;
}
/**
* PosAndCompare usage: if compare is zero, then a match was found, and
* pos is the insertion entry if compare < 0 and pos == 0 , then the
* search ended up less than the leftmost entry else compare > 0 , and
* the search will be to the immediate right of pos.
*
*
*
*/
// private void blockSearch(K k, PosAndCompare pc) {
// for (int i = 0; i < entries.size(); ++i) {
// pc.compare = comparator.compare(k, entries.get(i).k);
// if (pc.compare == 0) {
// pc.pos = i;
// return;
// }
// if (pc.compare < 0 && i == 0) {
// pc.pos = 0;
// return;
// }
//
// if (pc.compare < 0) {
// pc.pos = i - 1;
// pc.compare = 1;
// return;
// }
//
// }
// pc.pos = entries.size() - 1;
// pc.compare = 1;
//
// // binary search, it's hard to get it right !
// // int left = 0;
// // int right = entries.size();
// //
// // while (left <= right && left < entries.size()) {
// // // pc.pos = (right - left) / 2 + left;
// // pc.pos = (left + right) / 2;
// // pc.compare = comparator().compare(k, entries.get(pc.pos).k);
// // if (pc.compare < 0) {
// // right = pc.pos - 1;
// // } else if (pc.compare > 0) {
// // left = pc.pos + 1;
// // } else {
// // return;
// // }
// // }
// //
// // BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
// // pc.pos = Collections.binarySearch(entries, e, cmp);
//
// }
Comparator<BlockEntry<K, V>> cmp = new Comparator<BlockEntry<K, V>>() {
@Override
public int compare(BlockEntry<K, V> o1, BlockEntry<K, V> o2) {
// TODO Auto-generated method stub
return comparator.compare(o1.k, o2.k);
}
};
resultAndSplit<K, V> put(K k, V v) {
V v2;
if (entries.size() == 0) {
entries.add(new BlockEntry<K, V>(k, v));
return new resultAndSplit<K, V>(v);
} else {
// PosAndCompare pc = new PosAndCompare();
BlockEntry<K, V> e = new BlockEntry<K, V>(k, v);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
// blockSearch(k, pc);
// a match
if (res >= 0) {
v2 = entries.get(res).v;
entries.get(res).v = v;
return new resultAndSplit<K, V>(v2);
}
// follow leftBlock if search is to left of first entry
if (index == entries.size() && rightBlock != null) {
resultAndSplit<K, V> result = rightBlock.put(k, v);
if (result.splitNode != null) {
rightBlock = result.splitNode.right;
entries.add(result.splitNode.entry);
}
} else if (index == entries.size() && rightBlock == null
&& entries.size() == maxSz) {
rightBlock = new BTBlock<K, V>(this.maxSz, comparator);
resultAndSplit<K, V> result = rightBlock.put(k, v);
} else if (index < entries.size()
&& entries.get(index).left != null) {
// follow right block if it exists
resultAndSplit<K, V> result = entries.get(index).left.put(
k, v);
if (result.splitNode != null) {
entries.get(index).left = result.splitNode.right;
// add to the left
entries.add(index, result.splitNode.entry);
}
} else {
// add to the left
entries.add(index, e);
}
// check if overflowed block , split if it has.
if (entries.size() > maxSz) {
int mid = entries.size() / 2;
// copy right half to new entries list.
List<BlockEntry<K, V>> leftEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = 0; i < mid; ++i) {
leftEntries.add(entries.get(i));
}
BlockEntry<K, V> centreEntry = entries.get(mid);
BTBlock<K, V> leftBlock = new BTBlock<K, V>(maxSz,
comparator);
leftBlock.entries = leftEntries;
// the median entry's left block is the new left block's
// leftmost block
leftBlock.rightBlock = centreEntry.left;
// the new right block becomes the right block
centreEntry.left = leftBlock;
// reduce the old block's entries into its left half of
// entries.
ArrayList<BlockEntry<K, V>> newEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = mid + 1; i < entries.size(); ++i)
newEntries.add(entries.get(i));
this.entries = newEntries;
// create a return object, with the reduced old block as the
// left block
// and the median entry with the new right block attached
SplitRootEntry<K, V> split = new SplitRootEntry<K, V>(
centreEntry, this);
// the keyed value didn't exist before , so null
return new resultAndSplit<K, V>(split, null);
}
return new resultAndSplit<K, V>(v);
}
}
V get(K k) {
if (entries.size() == 0)
return null;
BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
if (res >= 0) {
return entries.get(res).v;
}
if (index == entries.size() && rightBlock != null) {
return rightBlock.get(k);
} else if (index < entries.size()
&& entries.get(index).left != null) {
return (V) entries.get(index).left.get(k);
} else
return null;
}
void getRange(SortedMap map, K k1, K k2) {
BlockEntry<K, V> e = new BlockEntry<K, V>(k1, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
BlockEntry<K, V> e2 = new BlockEntry<K, V>(k2, null);
int res2 = Collections.binarySearch(entries, e2, cmp);
int index2 = -res2 - 1;
int from = res >= 0 ? res : index;
int to = res2 >= 0 ? res2 : index2;
for (int i = from; i <= to; ++i) {
if (i < entries.size() && (i > from || res < 0)
&& entries.get(i).left != null) {
entries.get(i).left.getRange(map, k1, k2);
// if (pc2.pos == pc.pos)
// break;
}
if (i < to || res2 >= 0)
map.put(entries.get(i).k, entries.get(i).v);
if (i == entries.size() && rightBlock != null) {
rightBlock.getRange(map, k1, k2);
}
}
}
K headKey() {
if (rightBlock != null) {
return rightBlock.headKey();
}
return entries.get(0).k;
}
K tailKey() {
int i = entries.size() - 1;
if (entries.get(i).left != null) {
return (K) entries.get(i).left.tailKey();
}
return entries.get(i).k;
}
void show(int n) {
showTabs(n);
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
System.err.print("#" + i + ":(" + e.k + ":" + e.v + ") ");
}
System.err.println();
showTabs(n);
if (rightBlock != null) {
System.err.print("Left Block\n");
rightBlock.show(n + 1);
} else {
System.err.println("No Left Block");
}
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
showTabs(n);
if (e.left != null) {
System.err.println("block right of #" + i);
e.left.show(n + 1);
} else {
System.err.println("No block right of #" + i);
}
}
showTabs(n);
System.err.println("End of Block Info\n\n");
}
private void showTabs(int n) {
// TODO Auto-generated method stub
for (int i = 0; i < n; ++i) {
System.err.print(" ");
}
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
root.getRange(map, fromKey, toKey);
return map;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
// TODO Auto-generated method stub
return subMap(root.headKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
// TODO Auto-generated method stub
return subMap(fromKey, root.tailKey());
}
@Override
public K firstKey() {
// TODO Auto-generated method stub
return root.headKey();
}
@Override
public K lastKey() {
// TODO Auto-generated method stub
return root.tailKey();
}
@Override
public int size() {
// TODO Auto-generated method stub
return 0;
}
@Override
public boolean isEmpty() {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean containsKey(Object key) {
// TODO Auto-generated method stub
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
// TODO Auto-generated method stub
return false;
}
@Override
public V get(Object key) {
// TODO Auto-generated method stub
return root.get((K) key);
}
@Override
public V put(K key, V value) {
resultAndSplit<K, V> b = root.put(key, value);
if (b.splitNode != null) {
root = new BTBlock<K, V>(root.maxSz, root.comparator);
root.rightBlock = b.splitNode.right;
root.entries.add(b.splitNode.entry);
}
return b.v;
}
@Override
public V remove(Object key) {
// TODO Auto-generated method stub
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
// TODO Auto-generated method stub
}
@Override
public void clear() {
// TODO Auto-generated method stub
}
@Override
public Set<K> keySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
public class TestBtree {
private static final int N = 50000;
public static void main(String[] args) {
BTreeMap<Integer, Integer> map = new BTreeMap<Integer , Integer>();
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
map.setComparator(comparator);
List<Integer> testVals = new ArrayList<Integer>();
for (int i =0 ; i < N ; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i ) {
int x = r.nextInt(testVals.size());
x = testVals.remove(x);
//int x=i;
t.add(x);
map.put(x, x);
}
System.err.println("output " + N + " vals");
map.root.show(0);
for (int i = 0; i < N; ++i) {
int x = t.get(i);
if ( x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("Checked " + N + " entries");
}
}
一個 B+ 樹 Java 示例
[edit | edit source]實驗包括計時執行(例如 time java -cp . btreemap.BPlusTreeTest1),使用外部塊大小 + 1 大小的葉子塊大小,這樣它基本上只是底層的條目 TreeMap,與,例如,400 個內部節點大小,以及 200 個外部節點大小。其他實驗包括使用 SkipListMap 代替 TreeMap。
package btreemap;
import java.util.Collection;
import java.util.Comparator;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.SortedSet;
import java.util.TreeMap;
import java.util.TreeSet;
/**
* a B+ tree, where leaf blocks contain key-value pairs and
* internal blocks have keyed entries pointing to other internal blocks
* or leaf blocks whose keys are greater than or equal to the associated key.
*
* @author syan
*
* @param <K> key type implements Comparable
* @param <V> value type
*/
public class BPlusTreeMap<K, V> implements SortedMap<K, V> {
private int maxInternalBlockSize;
BPlusAnyBlock<K, V> root;
private int maxExternalSize;
BPlusTreeMap(int maxInternalSize, int maxExternalSize) {
this.maxInternalBlockSize = maxInternalSize;
this.maxExternalSize = maxExternalSize;
}
static class SplitOrValue<K, V> {
V v;
K k;
BPlusAnyBlock<K, V> left, right;
boolean split;
public boolean isSplit() {
return split;
}
public void setSplit(boolean split) {
this.split = split;
}
public SplitOrValue(V value) {
v = value;
setSplit(false);
}
public SplitOrValue(BPlusAnyBlock<K, V> left2,
BPlusAnyBlock<K, V> bPlusBlock) {
left = left2;
right = bPlusBlock;
k = right.firstKey();
setSplit(true);
// System.err.printf("\n\n** split occured %s**\n\n", bPlusBlock
// .getClass().getSimpleName());
}
}
static abstract class BPlusAnyBlock<K, V> {
public abstract SplitOrValue<K, V> put(K k, V v);
abstract SplitOrValue<K, V> splitBlock();
public abstract V get(K k);
public abstract boolean isEmpty();
public abstract K firstKey();
}
SortedSet<BPlusLeafBlock<K, V>> blockList = getLeafBlockSet();
SortedSet<BPlusLeafBlock<K, V>> getLeafBlockSet() {
// return new ConcurrentSkipListSet<BPlusLeafBlock<K, V>>();
return new TreeSet<BPlusLeafBlock<K, V>>();
}
static class BPlusLeafBlock<K, V> extends BPlusAnyBlock<K, V> implements
Comparable<BPlusLeafBlock<K, V>> {
SortedMap<K, V> entries = getEntryCollection();
static <K, V> SortedMap<K, V> getEntryCollection() {
return new TreeMap<K, V>();
}
int maxSize;
private BPlusTreeMap<K, V> owner;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusLeafBlock(BPlusTreeMap<K, V> bPlusTreeMap,
SortedMap<K, V> rightEntries) {
this.owner = bPlusTreeMap;
maxSize = owner.maxExternalSize;
entries = rightEntries;
}
public SplitOrValue<K, V> put(K k, V v) {
V v2 = entries.put(k, v);
if (entries.size() >= maxSize)
return splitBlock();
else
return new SplitOrValue<K, V>(v2);
}
public SplitOrValue<K, V> splitBlock() {
SortedMap<K, V> leftEntries = getEntryCollection();
SortedMap<K, V> rightEntries = getEntryCollection();
int i = 0;
for (Entry<K, V> e : entries.entrySet()) {
// System.out.println(this.getClass().getSimpleName() +
// " split entry " + e.getKey());
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
rightEntries.put(e.getKey(), e.getValue());
}
BPlusLeafBlock<K, V> right = createBlock(rightEntries);
// System.out.println("finished block split");
// System.out.println("\nleft block");
// for (K ik : leftEntries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\nright block");
// for (K ik : right.entries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private BPlusLeafBlock<K, V> createBlock(SortedMap<K, V> rightEntries) {
return owner.createLeafBlock(rightEntries);
}
@Override
public V get(K k) {
return entries.get(k);
}
@Override
public int compareTo(BPlusLeafBlock<K, V> o) {
return ((Comparable<K>) entries.firstKey()).compareTo(o.entries
.firstKey());
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
static class BPlusBranchBlock<K, V> extends BPlusAnyBlock<K, V> {
SortedMap<K, BPlusAnyBlock<K, V>> entries = createInternalBlockEntries();
int maxSize;
private BPlusAnyBlock<K, V> left;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusBranchBlock(int maxSize2) {
this.maxSize = maxSize2;
}
public SplitOrValue<K, V> put(K k, V v) {
BPlusAnyBlock<K, V> b = getBlock(k);
SplitOrValue<K, V> sv = b.put(k, v);
if (sv.isSplit()) {
entries.put(sv.k, sv.right);
if (entries.size() >= maxSize)
sv = splitBlock();
else
sv = new SplitOrValue<K, V>(null);
}
return sv;
}
BPlusAnyBlock<K, V> getBlock(K k) {
assert (entries.size() > 0);
BPlusAnyBlock<K, V> b = entries.get(k);
if (b == null) {
// headMap returns less than k
SortedMap<K, BPlusAnyBlock<K, V>> head = entries.headMap(k);
if (head.isEmpty()) {
b = left;
// System.out.println("for key " + k
// + " getting from leftmost block");
// showEntries();
} else {
b = entries.get(head.lastKey());
// System.out.println("for key " + k
// + " getting from block with key " + head.lastKey());
// showEntries();
}
}
assert (b != null);
return b;
}
public void showEntries() {
System.out.print("entries = ");
for (K k : entries.keySet()) {
System.out.print(k + " ");
}
System.out.println();
}
public SplitOrValue<K, V> splitBlock() {
Set<Entry<K, BPlusAnyBlock<K, V>>> ee = entries.entrySet();
int i = 0;
BPlusBranchBlock<K, V> right = new BPlusBranchBlock<K, V>(maxSize);
SortedMap<K, BPlusAnyBlock<K, V>> leftEntries = createInternalBlockEntries();
for (Entry<K, BPlusAnyBlock<K, V>> e : ee) {
// System.out.print("split check " + e.getKey() + ":"
// );
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
right.entries.put(e.getKey(), e.getValue());
}
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private SortedMap<K, BPlusAnyBlock<K, V>> createInternalBlockEntries() {
return new TreeMap<K, BPlusAnyBlock<K, V>>();
}
@Override
public V get(K k) {
BPlusAnyBlock<K, V> b = getBlock(k);
return b.get(k);
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
BPlusLeafBlock<K, V> b1 = getLeafBlock(fromKey);
BPlusLeafBlock<K, V> b2 = getLeafBlock(toKey);
SortedSet<BPlusLeafBlock<K, V>> range = blockList.subSet(b1, b2);
for (BPlusLeafBlock<K, V> b : range) {
SortedMap<K, V> m = b.entries.subMap(fromKey, toKey);
map.putAll(m);
}
return map;
}
private BPlusLeafBlock<K, V> getLeafBlock(K key) {
BPlusAnyBlock<K, V> b1;
b1 = root;
while (b1 instanceof BPlusBranchBlock<?, ?>) {
b1 = ((BPlusBranchBlock<K, V>) b1).getBlock(key);
}
return (BPlusLeafBlock<K, V>) b1;
}
public BPlusLeafBlock<K, V> createLeafBlock(SortedMap<K, V> rightEntries) {
BPlusLeafBlock<K, V> b = new BPlusLeafBlock<K, V>(this, rightEntries);
blockList.add(b);
return b;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
return subMap(firstKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
return subMap(fromKey, lastKey());
}
@Override
public K firstKey() {
return blockList.first().entries.firstKey();
}
@Override
public K lastKey() {
return blockList.last().entries.lastKey();
}
@Override
public int size() {
return (int) getLongSize();
}
private long getLongSize() {
long i = 0;
for (BPlusLeafBlock<K, V> b : blockList) {
i += b.entries.size();
}
return i;
}
@Override
public boolean isEmpty() {
return root.isEmpty();
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return false;
}
@Override
public V get(Object key) {
return (V) root.get((K) key);
}
@Override
public V put(K key, V value) {
if (root == null) {
SortedMap<K, V> entries = BPlusLeafBlock.getEntryCollection();
entries.put(key, value);
root = createLeafBlock(entries);
return null;
}
SplitOrValue<K, V> result = root.put(key, value);
if (result.isSplit()) {
BPlusBranchBlock<K, V> root = new BPlusBranchBlock<K, V>(
maxInternalBlockSize);
root.left = result.left;
root.entries.put(result.k, result.right);
this.root = root;
}
return result.v;
}
@Override
public V remove(Object key) {
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public void clear() {
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (BPlusLeafBlock<K, V> b : blockList) {
kk.addAll(b.entries.keySet());
}
return kk;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return null;
}
public void showLeaves() {
for (BPlusLeafBlock<K, V> b : blockList) {
System.out.println("Block");
for (Entry<K, V> e : b.entries.entrySet()) {
System.out.print(e.getKey() + ":" + e.getValue() + " ");
}
System.out.println();
}
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
/** driver program to test B+ tree */
public class BPlusTreeTest1 {
private static final int N = 1200000;
public static void main(String[] args) {
BPlusTreeMap<Integer, Integer> map = new BPlusTreeMap<Integer, Integer>(
400, 200 );// 5000002);
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
List<Integer> testVals = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i) {
int x = r.nextInt(N);
int z = testVals.set(x, testVals.get(0));
testVals.set(0, z);
}
for (int i = 0; i < N; ++i) {
map.put(testVals.get(i), testVals.get(i));
showProgress("put", testVals, i);
}
System.err.println("output " + N + " vals");
try {
for (int i = 0; i < N; ++i) {
showProgress("get", testVals, i);
int x = testVals.get(i);
if (x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("\nChecked " + N + " entries");
} catch (Exception e) {
// TODO: handle exception
e.printStackTrace();
map.showLeaves();
}
}
private static void showProgress(String label, List<Integer> testVals, int i) {
if (i % (N / 1000) == 0) {
System.out.printf("%s %d:%d; ", label, i, testVals.get(i));
if (i % (N / 10100) == 0)
System.out.println();
}
}
}
Treaps
[edit | edit source]二叉樹中的不變式是,左邊的鍵小於右邊的鍵。例如,對於具有順序的鍵,ord(L) < ord(R)。然而,這並沒有規定節點之間的關係,並且左右旋轉不會影響以上內容。因此,可以強加另一種順序。如果順序是隨機的,它很可能會抵消普通二叉樹的任何傾斜,例如,當按順序插入已經排序的輸入時。
下面是一個 Java 示例實現,包括一個普通二叉樹刪除程式碼示例。
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Random;
public class Treap1<K extends Comparable<K>, V> {
public Treap1(boolean test) {
this.test = test;
}
public Treap1() {}
boolean test = false;
static Random random = new Random(System.currentTimeMillis());
class TreapNode {
int priority = 0;
K k;
V val;
TreapNode left, right;
public TreapNode() {
if (!test) {
priority = random.nextInt();
}
}
}
TreapNode root = null;
void insert(K k, V val) {
root = insert(k, val, root);
}
TreapNode insert(K k, V val, TreapNode node) {
TreapNode node2 = new TreapNode();
node2.k = k;
node2.val = val;
if (node == null) {
node = node2;
} else if (k.compareTo(node.k) < 0) {
node.left = insert(k, val, node.left);
} else {
node.right = insert(k, val, node.right);
}
if (node.left != null && node.left.priority > node.priority) {
// left rotate
TreapNode tmp = node.left;
node.left = node.left.right;
tmp.right = node;
node = tmp;
} else if (node.right != null && node.right.priority > node.priority) {
// right rotate
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
}
return node;
}
V find(K k) {
return findNode(k, root);
}
private V findNode(K k, Treap1<K, V>.TreapNode node) {
if (node == null)
return null;
if (k.compareTo(node.k) < 0) {
return findNode(k, node.left);
} else if (k.compareTo(node.k) > 0) {
return findNode(k, node.right);
} else {
return node.val;
}
}
static class Deleted {
boolean success = false;
}
boolean delete(K k) {
Deleted del = new Deleted();
root = deleteNode(k, root, del);
return del.success;
}
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del) ;
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
public static void main(String[] args) {
LinkedList<Integer> dat = new LinkedList<Integer>();
for (int i = 0; i < 15000; ++i) {
dat.add(i);
}
testNumbers(dat, true); // no random priority balancing
testNumbers(dat, false);
}
private static void testNumbers(LinkedList<Integer> dat,
boolean test) {
Treap1<Integer, Integer> treap = new Treap1<>(test);
for (Integer integer : dat) {
treap.insert(integer, integer);
}
long t1 = System.currentTimeMillis();
Iterator<Integer> desc = dat.iterator();
int found = 0;
while (desc.hasNext()) {
Integer j = desc.next();
Integer i = treap.find(j);
if (j.equals(i)) {
++found;
}
}
long t2 = System.currentTimeMillis();
System.out.println("found = " + found + " in " + (t2 - t1));
System.out.println("test delete");
int deleted = 0;
for (Integer integer : dat) {
if (treap.delete(integer))
++deleted;
}
System.out.println("Deleted = " + deleted);
}
}
參考文獻
[edit | edit source]- William Ford 和 William Tapp。使用STL的C++資料結構。第 2 版。新澤西州上鞍河:普倫蒂斯·霍爾,2002 年。