離散數學/集合論/第 2 頁

冪集

一個集合 A 的冪集 是所有子集的集合（包括它本身和空集）。它表示為 P(A)。

使用集合推導符號，P(A) 可以定義為

P(A) = { Q | Q ⊆ A }

示例 4

如果 A 是

(a) A = {1, 2, 3}

(b) A = {1, 2}

(c) A = {1}

(d) A =ø

解

(a) P(A) = { {1, 2, 3}, {2, 3}, {1, 3}, {1, 2}, {1}, {2}, {3},ø }

(b) P(A) = { {1, 2}, {1}, {2},ø }

(c) P(A) = { {1},ø }

(d) P(A) = {ø }

冪集的基數

看看示例 4 中四個集合的基數，以及它們相應冪集的基數。它們是

	| A |	| P(A) |
(a)	3	8
(b)	2	4
(c)	1	2
(d)	0	1

很明顯，這裡有一個簡單的規律在起作用：用 2 的冪表示，冪集的基數分別是 2³、2²、2¹ 和 2⁰。

看起來我們發現了一個規律，如果 | A | = k，那麼 | P(A) | = 2^k。但我們能看出原因嗎？

好吧，A 的冪集的元素是 A 的所有可能的子集。任何一個這樣的子集都可以透過以下方式形成

• 選擇 A 的任何一個元素。我們可以決定將它包含在我們的子集中，也可以省略它。因此，處理 A 的第一個元素有 2 種方法。

• 現在選擇 A 的第二個元素。和以前一樣，我們可以將它包含在我們的子集中，也可以從我們的子集中省略它：同樣是處理該元素的 2 種方法。

• ...就這樣一直處理 A 的所有 k 個元素。

現在，組合學的基準原理告訴我們，如果我們能以 2 種方式完成 k 件事情中的每一件，那麼依次完成所有事情的總方法數為 2^k。

這些 2^k 種決策組合中的每一種——包含元素或省略元素——都會給我們 A 的一個不同的子集。因此，總共有 2^k 個不同的子集。

所以，如果 | A | = k，那麼 | P(A) | = 2^k。

集合論的基本規則

下面列出的定律 可以被稱為集合論的基本規則。我們透過回到交集、並集、全集和空集的定義，並考慮給定元素是否在一個或多個集合中，來推匯出這些定律。

冪等律

例如，我們將考慮“我第一次聽到你”定律——更準確地說，被稱為冪等律——它們指出

A ∩ A = A 並且 A ∪ A = A

如果你學習過邏輯，你可能對這條定律很熟悉。上述關係類似於重言式。

這些看起來很明顯，對吧？對這些定律的交集部分的一個簡單的解釋是這樣的

兩個集合 A 和 B 的交集定義為僅包含在 A 中且在 B 中的元素。如果我們在該定義中用 A 代替 B，我們得到 A 和 A 的交集是包含僅在 A 中且在 A 中的元素的集合。顯然，我們不需要重複說兩次（我第一次聽到你），所以我們可以簡單地說 A 和 A 的交集是 A 中的元素的集合。換句話說

A ∩ A = A

我們可以用類似的方式推匯出 A ∪ A = A 的解釋。

德摩根定律

有兩條定律，被稱為德摩根定律，告訴我們如何去掉括號，當括號外面有一個補符號——′——時。其中一條定律是這樣的

(A ∪ B) ′ = A ′ ∩ B ′

（如果你已經完成了練習 3，第 4 題，你可能已經從文氏圖中發現了這條定律。）

仔細看看這條定律是如何工作的。括號後的補符號在括號被移除時會影響括號內的所有三個符號

A 變為 A ′

B 變為 B ′

而 ∪ 變為 ∩。

為了證明這條定律，首先注意到，當我們定義子集時，我們說如果

A ⊆ B 並且 B ⊆ A，那麼 A = B

所以我們證明

(i) (A ∪ B) ′ ⊆ A ′ ∩ B ′

然後反過來

(ii) A ′ ∩ B ′ ⊆ (A ∪ B) ′

(i) 的證明是這樣的

讓我們隨機選取一個元素 x ∈ (A ∪ B) ′。我們對 x 一無所知；它可以是一個數字，一個函式，甚至是一頭大象。我們對 x 所知道的只是

x ∈ (A ∪ B) ′

所以

x ∉ (A ∪ B)

因為這就是補的含義。

這意味著 x 對你在 A 中嗎？和你在 B 中嗎？這兩個問題都回答否（否則它將在 A 和 B 的並集中）。因此

x ∉ A 並且 x ∉ B

再次使用補運算，我們得到

x ∈ A ′ 並且 x ∈ B ′

最後，如果一個東西在兩個集合中，它一定在它們的交集中，所以

x ∈ A ′ ∩ B ′

所以，我們從 (A ∪ B) ′ 中隨機選取的任何一個元素肯定都在 A ′ ∩ B ′ 中。因此，根據定義

(A ∪ B) ′ ⊆ A ′ ∩ B ′

(ii) 的證明類似

首先，我們從第一個集合中隨機選取一個元素，x ∈ A ′ ∩ B ′

使用我們對交集的瞭解，這意味著

x ∈ A ′ 並且 x ∈ B ′

所以，使用我們對補運算的瞭解，

x ∉ A 並且 x ∉ B

如果一個東西既不在 A 中也不在 B 中，它就不能在它們的並集中，所以

x ∉ A ∪ B

所以，最後

x ∈ (A ∪ B) ′

所以

A ′ ∩ B ′ ⊆ (A ∪ B) ′

我們現在已經證明了 (i) 和 (ii)，因此

(A ∪ B) ′ = A ′ ∩ B ′

這讓你體驗了這些定律背後的內容。所以，這裡列出了所有定律。

集合定律

交換律

A ∩ B = B ∩ A

A ∪ B = B ∪ A

結合律

(A ∩ B) ∩ C = A ∩ (B ∩ C)

(A ∪ B) ∪ C = A ∪ (B ∪ C)

分配律

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

冪等律

A ∩ A = A

A ∪ A = A

恆等律

A ∪ø= A

A ∩ U = A

A ∪ U = U

A ∩ø = ø

對合律 (A ′) ′ = A

補律

A ∪ A' = U

A ∩ A' =ø

U ′ =ø

ø′ = U

德摩根定律

(A ∩ B) ′ = A ′ ∪ B ′

(A ∪ B) ′ = A ′ ∩ B ′

對偶性與布林代數

您可能注意到以上集合定律成對出現：如果在任何給定的定律中，您將∪替換為∩，反之亦然（並且，如果需要，交換U和ø)，您將得到另一條定律。每對中的“夥伴定律”被稱為對偶，每條定律都是另一條定律的對偶。

• 例如，德摩根定律中的每一項都是另一項的對偶。

• 第一個補律，A ∪ A ′ = U，是第二個的對偶：A ∩ A ′ =ø.

• 等等。

這被稱為對偶原理。實際上，這意味著您只需要記住這張表格的一半！

這組定律構成了布林代數的公理。更多資訊請參見 布林代數。

使用集合定律的證明

我們可以使用這些定律 - 並且只有這些定律 - 來確定關於集合之間關係的其他陳述是真還是假。韋恩圖可能有助於暗示這些關係，但只有基於這些定律的證明才會被數學家認為是嚴謹的。

示例 5

使用集合定律，證明集合 (A ∪ B) ∩ (A ′ ∩ B) ′ 實際上與集合A相同。仔細說明您在每個階段使用的定律。

在開始證明之前，先說幾個“做”和“不要”

做從單個表示式 (A ∪ B) ∩ (A ′ ∩ B) ′ 開始，目標是將其簡單地更改為A。	不要從寫下整個等式 (A ∪ B) ∩ (A ′ ∩ B) ′ = A 開始 - 這就是我們必須得到的最終結果。
做一次只改變表示式的其中一部分，一次只使用一個集合定律。	不要省略步驟，一次改變兩件事。
做將等號彼此對齊。	不要讓您的工作變得雜亂無章且佈局混亂。
做說明您在每個階段使用的定律。	不要認為即使是最簡單的步驟也是理所當然的。

解

		使用的定律
(A ∪ B) ∩ (A ′ ∩ B) ′	= (A ∪ B) ∩ ((A ′) ′ ∪ B ′)	德摩根定律
	= (A ∪ B) ∩ (A ∪ B ′)	對合律
	= A ∪ (B ∩ B ′)	分配律
	= A ∪ø	補律
	= A	恆等律

我們現在已經證明了 (A ∪ B) ∩ (A ′ ∩ B) ′ = A，無論集合A和B包含什麼。像這樣的陳述 - 對A和B的所有值都為真的陳述 - 有時被稱為恆等式。

證明提示

這些證明沒有萬無一失的方法 - 練習是最好的指導。但這裡有一些一般性提示。

• 從等式中更復雜的一側開始，目標是將其簡化為另一側。

• 尋找分配律會導致簡化的位置（就像“普通”代數中的因式分解 - 請參閱上面的示例 5中的第三行）。

• 您可能需要使用德摩根定律來擺脫括號外的“符號”。

• 有時您可能需要“複雜化”一個表示式，然後才能對其進行簡化，正如下一個示例所示。

示例 6

使用集合定律證明A ∪ (A ∩ B) = A。

看起來很容易，是嗎？但是你可能會在這個問題上走很多彎路。（如果你喜歡，先嚐試一下，然後再閱讀下面的解決方案。）關鍵是首先“複雜化”它，將第一個A 寫成A ∩ U（使用恆等律之一）。

解

		使用的定律
A ∪ (A ∩ B)	= (A ∩ U) ∪ (A ∩ B)	恆等律
	= A ∩ (U ∪ B)	分配律
	= A ∩ (B ∪ U)	交換律
	= A ∩ U	恆等律
	= A	恆等律

集合論練習 4

點選連結檢視 集合論練習 4。

笛卡爾積

有序對

為了介紹這個主題，我們首先來看幾個使用我們之前提到的組合原理的例子（參見 基數）；即，如果事件R可以發生r種方式，而第二個事件S然後可以發生s種方式，那麼事件R和S依次發生的總方式數為r × s。這有時被稱為r-s 原理。

示例 7

選單

主菜

清蒸比目魚

烤羊肉

蔬菜咖哩

千層麵

甜點

新鮮水果沙拉

蘋果派

蛋糕

從上面的選單中可以選出多少種不同的套餐 - 主菜加甜點？

解

由於我們可以用四種方式選擇主菜，然後用三種方式選擇甜點來形成每次不同的組合，因此，使用r-s 原理，答案是共有 4 × 3 = 12 種不同的套餐。

示例 8

您正在準備出門。您有 5 條不同的（乾淨的！）內褲和兩條牛仔褲可供選擇。您可以用多少種方式選擇穿一條內褲和一條牛仔褲？

解

使用r-s 原理，有 5 × 2 = 10 種方式可以依次選擇這兩件衣服。

在以上兩種情況下，我們都有有序對的例子。顧名思義，有序對僅僅是一對以特定順序排列的“事物”。通常，選擇事物順序是任意的 - 我們只需要決定一種約定，然後堅持下去；有時順序實際上只有一種方式。

就套餐而言，大多數人選擇先吃主菜，然後吃甜點。在穿著的衣服中，我們在牛仔褲之前穿上內褲。您完全可以違背慣例，先吃甜點，然後吃主菜 - 或者將內衣穿在褲子上 - 但如果您這樣做，您將得到不同的有序對集。當然，您通常需要解釋很多！

組成有序對的兩個“事物”用圓括號括起來，並用逗號隔開；就像這樣

(千層麵，蛋糕)

如果您做過座標幾何，那麼您之前就遇到過有序對。例如，(2, 3) 表示x軸上向右移動 2 個單位，y軸上向上移動 3 個單位的點。在這裡，在數字的順序中也存在著一種約定：我們使用字母順序，將x座標放在y座標之前。（同樣，您可以選擇以相反的方式進行座標幾何，將y放在x之前，但是，您需要解釋很多！)

因此，使用集合符號，我們可以像這樣描述示例 7中的情況

M = {主菜}，D = {甜點}，C = {完整的套餐}。

那麼C可以寫成

C = { (m, d) | m ∈ M 且 d ∈ D }。

C被稱為集合積或笛卡爾積M和D，我們寫成

C = M × D

(讀作“C 等於 M 叉乘 D”)

假設示例 7中的選單擴充套件到包括開胃菜，可以是湯或果汁。現在可以選出多少種完整的套餐？

好吧，我們可以擴充套件r-s 原理以包含第三個選擇，並得到 2 × 4 × 3 = 24 種可能的套餐。

如果S = {湯，果汁}，那麼我們可以寫成

C = S × M × D

此集合的元素是有序三元組：(開胃菜，主菜，甜點)。因此，請注意，這些專案在三元組中出現的順序與它們被選擇的集合的順序相同：S × M × D 沒有給我們與 M × D × S 相同的有序三元組集。

有序n元組

一般來說，如果我們有n個集合：A₁, A₂, ..., A_n，那麼它們的笛卡爾積定義為

A₁ × A₂ × ... × A_n = { (a₁, a₂, ..., a_n) | a₁ ∈ A₁, a₂ ∈ A₂, ..., a_n ∈ A_n) }

而 (a₁, a₂, ..., a_n) 被稱為 有序n元組。

符號

A₁ × A₂ × ... × A_n 有時寫成

$\times _{i=1}^{n}$ A_i

笛卡爾平面

笛卡爾平面：圖8

你可能已經知道用有序對來表示平面上的一個點的方式。圖8中的圖表說明了一個笛卡爾平面，顯示了用有序對(5, 2)表示的點。

這些線被稱為軸：x軸和y軸。它們相交的點被稱為原點。點(5, 2)的位置如下：從原點開始；沿著x軸方向移動5個單位，然後沿著y軸方向移動2個單位。

使用集合符號

如果X = {x軸上的數字} 且 Y = {y軸上的數字}，那麼

(5, 2) ∈ X × Y

而且，事實上，如果X = {所有實數} 且 Y = {所有實數}，那麼X × Y作為一個整體代表了x-y平面中的所有點。

(這就是你有時會看到x-y平面被稱為R²的原因，其中R = {實數}。)
示例9

據信，如果A, B, P和Q是B ⊂ A 且 Q ⊂ P的集合，那麼

B × Q ⊂ A × P

使用仔細陰影和標記的笛卡爾圖來研究這個命題。

解

考慮到我們上面提到的X × Y中的有序對對應於x-y平面中的點，如果我們想在圖中表示A × P這樣的笛卡爾積，我們需要分別在x軸和y軸上將A和P表示為點集。

表示笛卡爾積A × P的區域是由x和y座標位於這些集合A和P內的點表示。像這樣

笛卡爾平面：圖9a

對於B和Q也可以說同樣的話：B必須位於x軸上，Q必須位於y軸上。

此外，由於B ⊂ A，因此我們必須將B表示為從A的元素中選擇的集合。類似地，由於Q ⊂ P，Q的元素必須位於P的元素內。

當我們在圖中新增這些元件時，它看起來像這樣

笛卡爾平面：圖9b

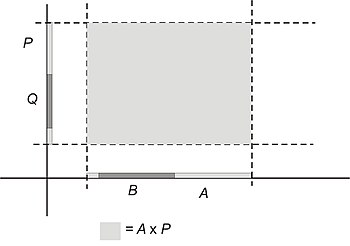
最後，當我們用一個矩形來表示集合B × Q，該矩形的限制由B和Q的限制決定，很明顯，這個矩形將位於表示A × P的矩形內

笛卡爾平面：圖9c

因此，命題B × Q ⊂ A × P似乎是正確的。

集合論習題5

點選連結以獲取集合論習題5。