離散數學/集合論

離散數學
← 介紹	集合論	集合論/頁面 2 →

維基百科在 集合論 中有相關資訊

介紹

集合論從一個簡單的開始：它考察一個物件是否屬於或不屬於一個集合，這個集合是透過某種明確的方式描述的。從這個簡單的開始，可以發展出一系列越來越複雜（而且有用！）的思想，這些思想導致了具有多種應用的符號和技術。

定義：集合

集合的當前定義可能聽起來很模糊。一個集合可以定義為實體的無序集合，這些實體由於遵循某個規則而相關聯。

'實體'可以是任何東西，字面上：數字、人、形狀、城市、文字片段，...等等

關於它們都遵循的'規則'的關鍵事實是它必須是明確定義的。換句話說，它必須清楚地描述實體遵循的內容。例如，如果我們談論的實體是單詞，則一個明確定義的規則是

X is English

一個沒有明確定義（因此不能用來定義集合）的規則可能是

X is hard to spell

其中 X 是任何單詞

元素

屬於給定集合的實體稱為該集合的元素。例如

Henry VIII is an element of the set of Kings of England. : kings of England {Henry VIII}

集合符號

要列出集合的元素，我們將它們用大括號括起來，並用逗號隔開。例如

 $\{-3,-2,-1,0,1,2,3\}$

集合的元素也可以用語言描述

 $\{{\text{ integers between }}-3{\text{ and  }}3{\text{ inclusive}}\}$

集合生成式符號可用於描述那些難以明確列出的集合。為了表示任何特定的集合，我們使用字母 $x$

 $\{x|x{\text{ is an integer and }}|x|<4\}$

或者等效地

 $\{x|x\in \mathbb {Z} ,|x|<4\}$

符號 $\in$ 和 $\notin$ 分別表示元素的包含和排除

 ${\text{dog }}\in \{{\text{quadrupeds}}\}$ 
 ${\text{Washington DC}}\notin \{{\text{European capital cities}}\}$

集合可以包含無限個元素，例如素數集合。省略號用於表示模式的無限延續

 $\{2,3,5,7,11,\dots \}$

請注意，省略號的使用可能會導致歧義，上面的集合可以被視為可被 4 整除的整數集合，例如。

集合通常用大寫字母表示： $A$ ， $B$ ，...
元素通常用小寫字母表示： $x$ ， $y$ ，...

特殊集合

全集

當前上下文中所有實體的集合稱為全集，或簡稱為宇宙。它用 $U$ 表示。

上下文可以是家庭作業練習，例如，其中全集被限制為其考慮的特定實體。此外，它可以是任何任意的問題，我們清楚地知道它在哪裡應用。

空集

不包含任何元素的集合稱為空集或空集。它用一對空括號表示： $\{\}$ 或符號 $\varnothing$ 表示。

定義一個不包含任何元素的集合可能看起來很奇怪。但是，請記住，人們可能會尋找問題的解決方案，在這些問題中，一開始並不清楚這些解決方案是否存在。如果事實證明沒有解決方案，那麼解決方案集將為空。

例如

如果 $U=\{{\text{words in the English language}}\}$ ，那麼 $\{{\text{words with more than 50 letters}}\}=\varnothing$ 。

如果 $U=\{{\text{whole numbers}}\}$ ，那麼 $\{x|x^{2}=10\}=\varnothing$ 。

空集的運算

對空集執行的運算（作為要操作的事物的集合）也可能令人困惑。（此類運算為空運算。）例如，空集元素的總和為零，但空集元素的乘積為一（參見空乘積）。這可能看起來很奇怪，因為空集沒有元素，那麼它們是加起來還是乘起來有什麼關係（因為“它們”不存在）？最終，這些運算的結果更多地反映了所討論的運算本身，而不是空集。例如，請注意，零是加法的單位元，而一是乘法的單位元。

特殊數字集

一些集合使用如此頻繁，以至於它們被賦予特殊的符號。

自然數

從 1 開始的“計數”數（或整數）稱為自然數。此集合有時用N表示。所以N = {1, 2, 3, ...}

注意，當我們用手寫這個集合時，我們不能用粗體型別寫，所以我們用黑板粗體字寫一個 N： $\mathbb {N}$

整數

所有整數，正數、負數和零構成整數集。它有時用Z表示。所以Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}

在黑板粗體中，它看起來像這樣： $\mathbb {Z}$

實數

如果我們將整數集擴充套件到包括所有小數，我們將形成實數集。實數集有時用R表示。

實數在小數點後可能有一個有限的數字（例如 3.625），或者一個無限的小數位數。在無限位數的情況下，這些位數可能

重複；例如 8.127127127...

... 或者它們可能不重複；例如 3.141592653...

黑板粗體： $\mathbb {R}$

有理數

那些小數位數有限或迴圈的實數稱為 *有理數*。有理數集合有時用字母 **Q** 表示。

有理數始終可以寫成精確的分數 *p*/ *q*；其中 *p* 和 *q* 是整數。如果 *q* 等於 1，則分數只是整數 *p*。注意，*q* 決不能等於零，因為此時該值將是未定義的。

例如：0.5、-17、2/17、82.01、3.282828... 都是有理數。

黑板粗體： $\mathbb {Q}$

無理數

如果一個數 *不能* 用分數 *p*/ *q* 精確表示，則稱其為 *無理數*。

例如：√2、√3、π。

集合論練習 1

點選連結檢視集合論練習 1

集合之間的關係

現在我們將研究集合之間可能存在的關係。

相等

兩個集合 $A$ 和 $B$ 被稱為 **相等** 當且僅當它們具有完全相同的元素。在這種情況下，我們簡單地寫

 $A=B$

注意關於相等集合的另外兩個事實

元素列出的 *順序* 無關緊要。

如果一個元素被 *列出多次*，則任何重複出現都將被忽略。

因此，例如，以下集合都是相等的

 $\{1,2,3\}=\{3,2,1\}=\{1,1,2,3,2,2\}$

（您可能想知道為什麼有人會寫出一個像 $\{1,1,2,3,2,2\}$ 的集合。您可能還記得，當我們定義 *空集* 時，我們注意到特定問題可能沒有解決方案，因此需要一個空集。好吧，在這裡，我們可能正在嘗試幾種不同的解決問題的方法，其中一些方法實際上會導致相同的解決方案。但是，當我們考慮 *不同的* 解決方案時，任何此類重複將被忽略。）

子集

如果集合 $A$ 的所有元素也是集合 $B$ 的元素，那麼我們說 $A$ 是 $B$ 的 *子集*，我們寫

 $A\subseteq B$

例如

在以下示例中

If  $T=\{2,4,6,8,10\}$  and  $E=\{{\text{even integers}}\}$ , then  $T\subseteq E$ 
If  $A=\{{\text{alphanumeric characters}}\}$  and  $P=\{{\text{printable characters}}\}$ , then  $A\subseteq P$ 
If  $Q=\{{\text{quadrilaterals}}\}$  and  $F=\{{\text{plane figures bounded by four straight lines}}\}$ , then  $Q\subseteq F$

請注意， $A\subseteq B$ 並不意味著 $B$ 必須包含不在 $A$ 中的額外元素；這兩個集合可以相等——正如 $Q$ 和 $F$ 在上面那樣。但是，如果此外 $B$ 確實包含至少一個不在 $A$ 中的元素，那麼我們稱 $A$ 是 $B$ 的 真子集。在這種情況下，我們將寫

 $A\subset B$

在上面的例子中

 $E$  contains ... -4, -2, 0, 2, 4, 6, 8, 10, 12, 14, ... , so  $T\subset E$

 $P$  contains $, ;, &, ..., so  $A\subset P$

但 $Q$ 和 $F$ 只是說同一件事的不同方式，所以 $Q=F$

使用 $\subset$ 和 $\subseteq$ ；顯然類似於在比較兩個數字時使用 < 和 ≤。

還要注意，每個集合都是全集的子集，而空集是每個集合的子集。

（你可能會對最後一句話感到好奇：空集怎麼可能成為任何東西的子集，因為它不包含任何元素？這裡的關鍵是，對於每個集合 $A$ ，空集不包含任何不在 $A$ 中的元素。所以 $\oslash \subseteq A$ 對於所有集合 $A$ 。）

最後，請注意，如果 $A\subseteq B{\text{ and }}B\subseteq A{\text{ then }}A$ 和 $B$ 必須包含完全相同的元素，因此相等。換句話說

 $A\subseteq B{\text{ and }}B\subseteq A{\text{ then }}A=B$

不相交

如果兩個集合沒有共同的元素，則稱它們為不相交。例如

If  $A=\{{\text{even numbers}}\}$  and  $B=\{1,3,5,11,19\}$ , then  $A$  and  $B$  are disjoint sets

維恩圖

維恩圖可以是說明集合之間關係的一種有用方法。

在維恩圖中

全集用一個矩形表示。矩形內的點代表全集中的元素；矩形外的點代表不在全集中的元素。你可以將這個矩形看作是一個'圍欄'，將不需要的東西擋在外面，並將我們的注意力集中在我們正在討論的事情上。

其他集合用迴圈表示，通常是橢圓形或圓形，繪製在矩形內。同樣，給定迴圈內的點代表它所代表的集合中的元素；迴圈外的點代表不在集合中的元素。

在左側，集合A和B是不相交的，因為迴圈沒有重疊。

在右側，A是B的子集，因為表示集合A的迴圈完全被迴圈B包圍。

維恩圖：實戰示例

示例 1

圖 3表示一個維恩圖，它顯示了兩個集合A和B，在一般情況下，對集合之間的任何關係一無所知。

注意，表示全集的矩形被分成四個區域，分別標記為i、ii、iii和iv。

如果結果表明，關於集合A和B，可以說什麼

(a) 區域ii為空？

(b) 區域iii為空？

(a) 如果區域ii為空，那麼A不包含任何不在B中的元素。所以A是B的子集，圖應該像上面的圖 2一樣重新繪製。

(b) 如果區域iii為空，那麼A和B沒有共同的元素，因此是不相交的。然後圖應該像上面的圖 1一樣重新繪製。

示例 2

(a) 畫一個維恩圖來表示三個集合A、B和C，在一般情況下，對集合之間可能的任何關係一無所知。

(b) 現在表示U的矩形被分成多少個區域？

(c) 當這些區域的各種組合為空時，討論集合A、B和C之間的關係。

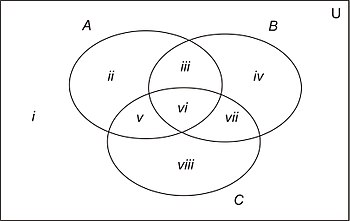
(a) 圖 4中的圖顯示了三個集合的一般情況，其中對它們之間任何可能的關係列一無所知。

(b) 表示U的矩形現在被分成 8 個區域，用羅馬數字i到viii表示。

(c) 可能存在各種空的區域組合。在每種情況下，都可以重新繪製維恩圖，以使空的區域不再包含在內。例如

如果區域ii為空，則表示A的迴圈應該變小，並移動到B和C內部以消除區域ii。

如果區域ii、iii和iv為空，則使A和B變小，並將它們移動，使它們都位於C內部（從而消除所有這三個區域），但以一種方式這樣做，使它們仍然相互重疊（從而保留區域vi）。

如果區域iii和vi為空，則'拉開'迴圈A和B以消除這些區域，但保持每個迴圈與迴圈C重疊。

……等等。繪製上述每個示例的維恩圖留作讀者的練習。

示例 3

定義以下集合

U = {1, 2, 3, …, 10}

A = {2, 3, 7, 8, 9}

B = {2, 8}

C = {4, 6, 7, 10}

使用下面描述的兩階段技術，繪製一個維恩圖來表示這些集合，並在適當的區域標記所有元素。

該技術如下

繪製一個'一般'的 3 集合維恩圖，類似於示例 2中的圖。

一次只遍歷全集中的元素，每次只遍歷一次，將每個元素輸入圖的適當區域。

如果需要，重新繪製圖，將迴圈彼此移動或分開以消除任何空的區域。

不要從輸入集合A的元素開始，然後是集合B，然後是集合C – 你可能會錯過元素或將它們包含兩次！

解決方案

在繪製三個空迴圈的圖後，它看起來像圖 4（但沒有羅馬數字！），遍歷U中的十個元素 - 數字 1 到 10 - 對每個元素問三個問題；就像這樣

第一個元素：1

你在A中嗎？不

你在B中嗎？不

你在C中嗎？不

對所有三個問題的回答都是'否'，這意味著數字 1 在所有三個迴圈之外。所以在適當的區域（圖 4中的區域編號i）中寫入它。

第二個元素：2

你在A中嗎？是

你在B中嗎？是

你在C中嗎？不

是，是，否：所以數字 2 在A和B內，但在C之外。然後放在區域iii中。

……以此類推，對元素 3 到 10 進行操作。

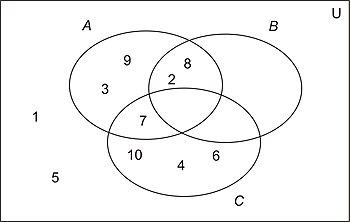
生成的圖看起來像圖 5。

最後一步是檢查圖中是否存在空的區域 - 在這種情況下，我們稱之為圖 4中的iv、vi和vii區域 - 然後重新繪製圖以消除這些區域。當我們這樣做時，我們將清楚地看到三個集合之間的關係。

所以我們需要

拉開B和C，因為它們沒有共同的元素。

將B推到A內，因為它在A之外沒有元素。

最終結果如圖6所示。

維恩圖中的區域和真值表

也許你已經意識到，在維恩圖中新增一個額外的集合會使表示全集的矩形被劃分的區域數量加倍。這給了我們一個非常簡單的模式，如下所示

使用一個集合迴圈，將只有兩個區域：迴圈的內部和外部。

使用兩個集合迴圈，將有四個區域。

使用三個迴圈，將有八個區域。

……等等。

不難理解為什麼應該是這樣。我們在圖中新增的每個新迴圈都會將每個現有區域分成兩個，從而將區域總數加倍。

在A中嗎？	在B中嗎？	在C中嗎？
Y	Y	Y
Y	Y	N
Y	N	Y
Y	N	N
N	Y	Y
N	Y	N
N	N	Y
N	N	N

但還有另一種看待這個問題的方法，那就是，在上面示例 3的解決方案中，我們對每個元素問了三個問題：你在 A 中嗎？你在 B 中嗎？和你在 C 中嗎？現在，對每個問題顯然有兩個可能的答案：是和否。當我們將這些問題的答案組合在一起時，一個接一個，那麼總共有 2³ = 8 種可能的答案集。這八種可能的答案組合中的每一種都對應於維恩圖上的一個不同區域。

完整的答案集非常類似於一個真值表 - 這是邏輯中的一個重要概念，它處理可能為真或假的語句。右側的表格顯示了 3 個集合A、B和C的八種可能的答案組合。

你會發現研究每列中 Y 和 N 的模式會很有幫助。

當你向下閱讀C列時，字母在每一行都會改變：Y、N、Y、N、Y、N、Y、N

向下閱讀B列時，字母在每隔一行都會改變：Y、Y、N、N、Y、Y、N、N

向下閱讀A列時，字母每四行都會改變：Y、Y、Y、Y、N、N、N、N

集合論練習 2

點選連結檢視集合論練習 2

集合運算

正如我們可以用“加”、“減”、“乘”和“除”等運算將兩個數字組合成第三個數字一樣，我們也可以用多種方法將兩個集合組合成第三個集合。我們將再次從維恩圖開始，維恩圖展示了兩個集合 *A* 和 *B* 的一般位置，我們對它們之間可能的關係沒有任何資訊。

在A中嗎？	在B中嗎？	區域
Y	Y	iii
Y	N	ii
N	Y	iv
N	N	i

右側表格中的前兩列顯示了對兩個集合 *A* 和 *B* 的問題“你在 *A* 中嗎？”和“你在 *B* 中嗎？”的四種可能的答案集合；第三列中的羅馬數字顯示了 *圖 7* 中維恩圖中對應的區域。

交集

兩個迴圈重疊的區域 *iii*（對應於“是”後跟“是”的區域）稱為集合 *A* 和 *B* 的 *交集*。它用 *A* ∩ *B* 表示。所以我們可以將交集定義如下

兩個集合 *A* 和 *B* 的 *交集*，寫成 *A* ∩ *B*，是屬於 *A* **且** 屬於 *B* 的元素的集合。

（請注意，在符號邏輯中，一個類似的符號， $\scriptstyle \wedge$ ，用於用 **AND** 運算子連線兩個邏輯命題。）

例如，如果 *A* = {1, 2, 3, 4} 且 *B* = {2, 4, 6, 8}，則 *A* ∩ *B* = {2, 4}。

那麼，我們可以說，我們已經使用 *交集運算* 將兩個集合組合成第三個集合。

並集

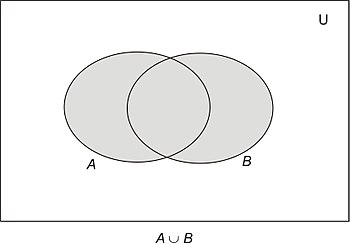
以類似的方式，我們可以將兩個集合的 *並集* 定義如下

兩個集合 *A* 和 *B* 的 *並集*，寫成 *A* ∪ *B*，是屬於 *A* **或** 屬於 *B*（或兩者都屬於）的元素的集合。

然後，並集由 *圖 7* 中的區域 *ii*、*iii* 和 *iv* 表示。

（再次，在邏輯中，一個類似的符號， $\scriptstyle \vee$ ，用於用 **OR** 運算子連線兩個命題。）

因此，例如，{1, 2, 3, 4} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}。

然後你會看到，為了進入交集，一個元素必須對 *兩個* 問題都回答“是”，而為了進入並集，*任何一個* 答案都可以是“是”。

∪ 符號看起來像“並集”的首字母，也像一個可以容納很多物品的杯子。 ∩ 符號看起來像一個灑了的東西的杯子，不能容納很多物品，或者可能是“n”，代表“交集”。注意不要混淆這兩個符號。

差集

兩個集合 *A* 和 *B* 的 *差集*（也稱為 *A* 和 *B* 的 *集合論差集*，或 *B* 在 *A* 中的 *相對補集*）是 **屬於** *A* **但不屬於** *B* 的元素的集合。

這寫成 *A* - *B*，或者有時寫成 *A* \ *B*。

然後，差集中的元素是那些對第一個問題“你在 *A* 中嗎？”回答“是”，但對第二個問題“你在 *B* 中嗎？”回答“否”的元素。這種答案組合位於上述表格的第 2 行，對應於 *圖 7* 中的區域 *ii*。

例如，如果 *A* = {1, 2, 3, 4} 且 *B* = {2, 4, 6, 8}，則 *A* - *B* = {1, 3}。

補集

到目前為止，我們已經考慮了 *兩個* 集合組合成第三個集合的運算：*二元* 運算。現在我們來看一個 *一元* 運算，它只涉及 *一個* 集合。

**不** 屬於集合 *A* 的元素的集合稱為 *A* 的 *補集*。它寫成 *A*′（或者有時寫成 *A*^C，或 ${\bar {A}}$ ）。

顯然，這是對問題“你在 *A* 中嗎？”回答“否”的元素的集合。

例如，如果 **U** = **N** 且 *A* = {奇數}，則 *A*′ = {偶數}。

請注意 *補集* 這個詞的拼寫：它的字面意思是“互補的專案或物品”；換句話說，“完成”的東西。所以，如果我們已經有了 *A* 的元素，*A* 的補集就是 *完成* 全集的集合。

集合運算的性質

1. 交換律

$A\cup B=B\cup A$

$A\cap B=B\cap A$

2. 結合律

$A\cup (B\cup C)=(A\cup B)\cup C$

$A\cap (B\cap C)=(A\cap B)\cap C$

3. 分配律

$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

4. 補集的特殊性質

$(A')'=A$

$U'=\phi$

$\phi '=U$

$A\cap B'=A-B$

5. 德·摩根定律

$(A\cap B)'=A'\cup B'$

$(A\cup B)'=A'\cap B'$ .

總結

交集：屬於A和屬於B的元素	並集：屬於A或屬於B（或兩者都屬於）的元素
差集：屬於A而不屬於B的元素	對稱差集：屬於A或屬於B但不屬於兩者的元素
補集：不屬於A的元素