分形/共形對映

共形對映

以下是共形對映應用於圖片的例子。這種技術是域著色的推廣，其中域空間不是由固定的無限色輪著色，而是由一個有限的圖片平鋪平面。教學上的意義在於有一個來自網路攝像頭的圖片流，允許更多的互動性和更豐富的反饋迴圈。

共形對映

一個鐘錶的圖片。

一個鐘錶經過相似變換後的圖片。

共形對映是保持角度的平面變換。平面可以用笛卡爾座標系引數化，其中一個點表示為$(x,y)\in \mathbb {R} ^{2}$，但對於共形對映，最好將它理解為複平面，其中點表示為$x+i\,y\in \mathbb {C}$.

在復座標系中，乘以一個實數r對應一個同質變換，乘以一個單位數$e^{i\theta }$對應一個角度為θ的旋轉，乘以一個通用的複數$z=r\,e^{i\theta }$對應一個相似對映。

全純函式是一個共形對映，因為它在區域性是一個相似對映$f(z)=a\,(z-z_{0})+b+o(z-z_{0})$，其中$a=f'(z_{0})$是導數，$b=f(z_{0})$是f在z₀的值。導數是變換的區域性縮放因子。

在相似性之後，相似性具有常數導數函式，多項式，特別是單項式$z\mapsto z^{k}$是最簡單的全純函式。它的導數是$z\mapsto k\,z^{k-1}$，它在原點為零；因此，相關的對映只有在遠離原點時才是共形的。

我們面臨的一個問題是，全純函式通常不是單射的：例如，考慮單項式$z^{k}$，例如，k個不同的點被對映到同一個值。

考慮到用鐘錶圖片平鋪的平面，當平方時，它變成以下模糊的圖片

一個鐘錶平方。注意每個點都被覆蓋了兩次。

我們看到，中心圓盤是全域性儲存的，被對映到自身，但每個點（除了零）都被覆蓋了兩次，使得圖片變得模糊。例如，+1（在 3 點鐘位置）和 −1（在 9 點鐘位置）都被髮送到 +1（在中間右側），+i（中午）和 i（6 點鐘位置）都被髮送到 −1（在中間左側）。

為了獲得一個單射應用，我們可以將自己限制在例如正實半平面或負實半平面。

負實半平面平方。

正實半平面平方。

從更遠的地方看，我們得到了整個平鋪的相同大圖。

• 
  負實半平面平方。
• 
  鐘錶平方：共形但不是單射。
• 
  正實半平面平方。

拉回

鹽度被描繪成一個原像

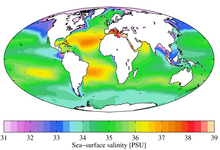
為了獲得一個漂亮的共形圖片，考慮不是直接像而是原像會更容易更自然。

這正是許多地球資訊被描繪的方式。例如，將溫度值設定為每個點的地圖可以透過將地球儀上的每個點用顏色繪製來描繪，該顏色指定該點溫度函式的值。目標空間，即溫度空間，從藍色（較小值）到紅色（較大值）被繪製。這裡使用了相同的繪圖技術，但目標空間不再是 1 維實數空間；它不是一條線，而是整個平面。

圖片不再表示應用程式的域，而是它的目標空間。點 z 根據畫素 f(z) 著色。

由 $z\mapsto z^{2}$ 進行的反向對映。

注意重複：點 z 和 −z 被著色相同，因為它們都被對映到同一個影像 z²。

一個 4 次多項式。注意它導數的零點。簡單的零點看起來沒什麼特別。

由 $z\mapsto z^{3}$ 進行的反向對映。

同樣，k 階單項式將 k 個不同的點對映到同一個影像。

可以透過描繪它的反向對映來理解關於保角對映的許多有用資訊。由於正向縮放因子是導數，反向縮放因子是導數的“逆”。因此，在函式導數的零點處發生了一些非常特殊的事情，縮放因子變得無窮大，並且它顯示出來了。此外，零點的階數可以透過特徵圍繞奇點的重複次數來讀出。我們也注意到，當導數為實數且為正時，圖片是“直立”的，而當導數為實數且為負時，圖片是“倒置”的。當我們將自己限制在實軸上時，我們可以找出實函式圖形的草圖。我們也注意到拐點是縮放因子的最小值或最大值。

反演，極點

在全純函式之後，區域性保角對映還包括亞純函式，並且它們的極點的位置和階數可以讀出。

反演 $z\mapsto 1/z$.

反演（詳細檢視）。

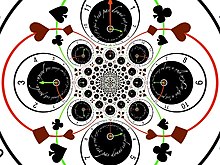
反演 $z\mapsto 1/z$ 在零點處有一個簡單的極點。它是一個莫比烏斯變換 $z\mapsto {\frac {az+b}{cz+d}}$，其中 a、b、c 和 d 是四個複數，使得 $ad-bc\neq 0$，因此它將圓和線對映到圓和線。特別是，水平線和垂直線變成了過零點的圓。反演交換了單位圓的內部和外部。

兩個極點在 ±1/2。

一個二階極點 $z\mapsto 1/z^{2}$.

像零點一樣，極點的階數也可能高於簡單極點。圓一般情況下只是無窮小地被保留。我們可以將高階極點視為幾個簡單極點彙集在一起。

對數和指數

指數對映 $z\mapsto e^{z}$。注意同態和旋轉不變性，對應於目標格子的水平（實數）和垂直（純虛數）平移不變性。

對數對映 $z\mapsto \log(z)$。注意單位圓被垂直地解開。

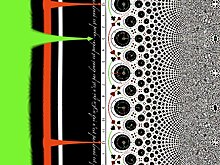
複分析和地圖學中一個非常重要的對映是從直角座標 (x,y) 到極座標 (r,θ) 的變換。這個變換是由對數/指數函式對實現的，它們互為倒數 ($\log(\exp(z))=z$)。實際上，

$\log(r\,e^{i\theta })=\log(r)+i\theta$ 將 (r, θ) 對映到 (x = log(r), y = θ)，而 $\exp(x+i\,y)=\exp(x)\,e^{i\,y}$ 將 (x, y) 對映到 (r = exp(x), θ = y)。

在圖中，對數將以原點為中心的圓展開成垂直線，並將射線對映到水平線。相反，指數將垂直線包裹成同心圓，並將水平線對映到透過原點的射線。請注意，對數在零處趨於無窮大，但其增長速度比反演慢得多。

改變格子的基底，可以得到螺旋變化。作為極點和零點，可以新增對數奇點。

• 
• 
• 
• 

本質奇點

本質奇點 $z\mapsto e^{1/z}$.

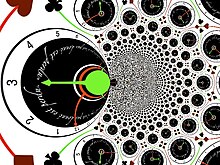
解析函式會遇到另一種型別的奇點，例如本質奇點 $z\mapsto e^{1/z}$ 在 $z=0^{-}$ 為零，並具有零點累積，在 $z=0^{+}$ 具有極點累積。

收斂半徑

解析函式可以求和成冪級數。在給定點，其泰勒級數具有收斂半徑。比較函式及其截斷泰勒級數的反向對映，我們可以說明這個概念。

• 
  正切函式在每個 kπ/2 處有一個簡單的極點。它在無窮遠處有一個本質奇點。
• 
  它在 0 處的 7 階泰勒級數在其收斂圓盤中是一個很好的近似。

程式

• Don Marshall 的 zipper
• ConformalMaps，Samuel S. Watson 在 Julia 中編寫
• 使用 Zipper 演算法數值逼近共形對映
• RoyWiggins 實現的 Julia 包，用於數值共形對映的 zipper 演算法

外部連結

• 維基百科中的共形對映類別
• 這些圖片使用以下方式變形 Java 小程式；另一個 版本 可用於 Mac OS X，它可以變形來自網路攝像頭的影片流。java -d32 -jar ComplexMap.jar。這很有趣。使用 Java 實驗數學工具 庫。
• John H. Mathews 的共形對映模組
• 許多共形對映的互動式視覺化
• 用於視覺化共形對映的 Java 小程式
• 共形對映，Michael Trott，Wolfram 演示專案。
• Java 小程式，Jürgen Richter-Gebert 使用 Cinderella。
• 共形網路攝像頭 基於 Cinderella。使用您的網路攝像頭以互動方式繪製本頁上的示例，使用您的網路攝像頭饋送。
• conformal_map，Yue Liu 編寫的

另請參見

• 對圓盤進行平方運算的解析方法
• 梅比烏斯變換