分形/莫比烏斯變換

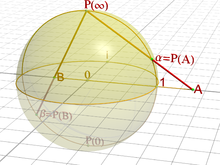
黎曼球面

莫比烏斯變換是平面變換的一個例子

定義

莫比烏斯變換 是擴充套件複平面的有理函式 f，其形式為

$f(z)={\frac {az+b}{cz+d}}$

其中復變數 z 為複數。

這裡係數 a, b, c, d 和結果 w 是複數，滿足

$ad-bc\neq 0$

$w=f(z)={\frac {az+b}{cz+d}}$

表示形式

• 函式
• 矩陣

函式

$f(z)={\frac {az+b}{cz+d}}$

$f\ \colon z\to w$

$w=f(z)$

矩陣

使用齊次座標的矩陣形式:

$M=\left({\begin{matrix}{\begin{array}{cc}a&b\\c&d\end{array}}\end{matrix}}\right)\,$

$w=\left({\begin{matrix}{\begin{array}{c}w\\1\end{array}}\end{matrix}}\right)=\left({\begin{matrix}{\begin{array}{cc}a&b\\c&d\end{array}}\end{matrix}}\right)\left({\begin{matrix}{\begin{array}{c}z\\1\end{array}}\end{matrix}}\right)=\left({\begin{matrix}{\begin{array}{c}az+b\\cz+d\end{array}}\end{matrix}}\right)\,}$

矩陣 M 是一個 2x2 可逆方陣

示例

• 使用複數進行變換
  • 梅比烏斯變換
    • 論文：看起來像圓形的正方形：由 Saul Schleimer 和 Henry Segerman 對球形影像進行變換 和 Shadertoy : 球形影像 by soma_arc 和 python 程式碼 Henry Segerman
• 梅比烏斯變換在 mandelbrot-graphics 庫中
• Kleinian 群分形的數學 by hiddendimension
• 廣義圓和梅比烏斯變換 by Stéphane Laurent
• 射影變換和梅比烏斯變換 by Tadao Ito

簡單

以下簡單的變換也是梅比烏斯變換

• $f(z)=z\quad (a=1,b=0,c=0,d=1)$ 是一個恆等變換
• $f(z)=z+b\quad (a=1,c=0,d=1)$ 是一個平移變換
• $f(z)=az\quad (b=0,c=0,d=1)$ 是一個相似變換和旋轉變換的組合。
  • 如果 $|a|=1$ 那麼它就是一個旋轉變換
  • 如果 $a\in \mathbb {R}$ 那麼它就是一個相似變換
• $f(z)=1/z\quad (a=0,b=1,c=1,d=0)$ 反演變換和關於實軸的對稱變換

如何...?

特徵值和特徵向量

一個數 $\lambda$ 和一個非零向量 $v$ 滿足

$Mv=\lambda v$

分別稱為矩陣 M 的特徵值 和特徵向量。

對於二維空間，存在包含根式的公式，可用於求解特徵值。可以使用二次方程求解特徵值

$\lambda _{\pm }={\frac {{\rm {tr}}(M)\pm {\sqrt {{\rm {tr}}^{2}(M)-4\det(M)}}}{2}}.$

對角化

一個對角矩陣是一個矩陣，其中主對角線之外的元素都為零。換句話說，對角矩陣中所有非對角元素都為零。

矩陣 $A$ 的主對角線是指元素列表 $A_{i,j}$，其中 $i=j$，這裡 $a_{11},a_{22}$

矩陣 M 的對角化給出矩陣對：D、P，使得：

• D 是對角矩陣（所有非對角元素為 0）
• $M=PDP^{-1}$

對於 2x2 矩陣，存在一個簡單的封閉形式解

與標量的乘積

如果 A 是一個矩陣，而 c 是一個標量，則矩陣 $c\mathbf {A}$ 和 $\mathbf {A} c$ 是透過將 A 中所有元素的左側或右側乘以 c 得到的。

跡

2x2 方陣 $\mathbf {A}$ 的跡 $\operatorname {tr}$

$\mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}}$

是其對角元素的總和

$\operatorname {tr} (\mathbf {A} )=\sum _{i=1}^{2}a_{ii}=a_{11}+a_{22}$

因此 $\operatorname {tr} (\mathbf {M} )=a+d$

行列式

矩陣 $\mathbf {M}$ 的行列式 $\operatorname {det}$

$\operatorname {det} \mathbf {M} =\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}=ad-bc$

逆變換

透過逆變換 w=Sz=1/z（原始莫比烏斯變換）對映廣義圓。直線對映到圓/直線。

逆莫比烏斯變換

$\mathbf {M} ^{-1}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}^{-1}={\frac {1}{\operatorname {det} \mathbf {M} }}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}={\frac {1}{ad-bc}}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}$

$z={\frac {1}{\operatorname {det} \mathbf {M} }}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}{\begin{pmatrix}w\\1\end{pmatrix}}$

$z=f^{-1}(w)$.

插值

如何平滑地插值莫比烏斯變換？

如果您有兩個表示為

$f(z)={\frac {az+b}{cz+d}}$

$g(z)={\frac {pz+q}{rz+s}}$

的莫比烏斯變換，其中係數是複數

$a,b,c,d,p,q,r,s,z\in \mathbb {C}$

是否可以推匯出第三個函式 $h(z,t)$，其中 $t\in \mathbb {R}$ 且 $0\leq t\leq 1$，它“平滑地”插值 $f(z)$ 和 $g(z)$ 所表示的變換？

解

$h(z,t)=fe^{t\log(f^{-1}g)}=f\operatorname {exp} (t\log(f^{-1}g))$

透過三個點指定變換

給定黎曼球面（我們稱之為 z 球面）上的三個不同點z₁、z₂、z₃，以及另一個球面（w 球面）上的另外三個不同點w₁、w₂、w₃，則存在一個唯一的莫比烏斯變換f(z)，其滿足：

• $f(z_{i})=w_{i}$
• $f^{-1}(w)=z_{i}$

對於i=1,2,3

對映到 0, 1, 無窮大

具有顯式公式的莫比烏斯變換為：

$f(z)={\frac {(z-z_{1})(z_{2}-z_{3})}{(z-z_{3})(z_{2}-z_{1})}}$

對映：

• z₁ 到 w₁= 0
• z₂ 到 w₂= 1
• z₃ 到 w₃= ∞

單位圓到實軸 - 第一種方法

讓我們在圓上選擇 3 個 z 點：

• z₁= -1
• z₂= i
• z₃= 1

那麼莫比烏斯變換將為：

$f(z)={\frac {(z+1)(i-1)}{(z-1)(i+1)}}$

已知：

$i+1=-i(i-1)$

可以將其簡化為：

$f(z)=i{\frac {z+1}{z-1}}$

在Maxima CAS中，可以進行以下操作：

(%i1) rectform((z+1)*(%i-1)/((z-1)*(%i+1)));
(%o1) (%i*(z+1))/(z−1)

其中一般形式的係數為：

$a=i$

$b=i$

$c=1$

$d=-1$

因此可以使用一般形式計算逆函式：

$f^{-1}(w)={\frac {dw-b}{-cw+a}}={\frac {-i-w}{i-w}}$

讓我們使用 Maxima CAS 檢查一下：

(%i3) fi(w):=(-%i-w)/(%i-w);
(%o3) fi(w):=−%i−w/%i−w
(%i4) fi(0);
(%o4) −1
(%i5) fi(1);
(%o5) −%i−1/%i−1
(%i6) rectform(%);
(%o6) %i

查詢如何在沒有符號計算程式 (CAS) 的情況下進行計算：

(%i3) fi(w):=(-%i-w)/(%i-w);
(%o3) fi(w):=−%i−w/%i−w
(%i8) z:x+y*%i;
(%o8) %i*y+x
(%i9) z1:fi(w);
(%o9) (−%i*y−x−%i)/(−%i*y−x+%i)
(%i10) realpart(z1);
(%o10) ((−y−1)*(1−y))/((1−y)^2+x^2)+x^2/((1−y)^2+x^2)
(%i11) imagpart(z1);
(%o11) (x*(1−y))/((1−y)^2+x^2)−(x*(−y−1))/((1−y)^2+x^2)
(%i13) ratsimp(realpart(z1));
(%o13) (y^2+x^2−1)/(y^2−2*y+x^2+1)
(%i14) ratsimp(imagpart(z1));
(%o14) (2*x)/(y^2−2*y+x^2+1)

將曼德勃羅集主心形展開兩步：莫比烏斯對映和共形對映

將曼德勃羅集主心形展開到週期 7-13

因此使用符號：

$z=x+yi=f^{-1}(w)$

得到：

$x=\operatorname {Re} (z)=\operatorname {Re} (f^{-1}(w))={\frac {y^{2}+x^{2}-1}{y^{2}-2y+x^{2}+1}}$

$y=\operatorname {Im} (z)=\operatorname {Im} (f^{-1}(w))={\frac {2x}{y^{2}-2y+x^{2}+1}}$

它可用於展開曼德勃羅集的成分

單位圓到實軸 - 第二種方法

函式 

$f(z)=i{\frac {z-1}{z+1}}$

將單位圓對映到實軸 

• z=1 到 w=0
• z=i 到 w=1
• z=-1 到 $w=\infty$

對映到虛軸

函式 $f(z)={\frac {z-1}{z+1}}$ 將單位圓對映到虛軸。

視覺化

• 由 Mark McClure 展現的莫比烏斯變換
• 由 Tim Hutton 提供的即時演示
• 由 Tim Hutton 提供的莫比烏斯變換迭代

參考文獻

• 由 Claude Heiland-Allen 提供的莫比烏斯變換