分形/計算機圖形技術/2D/變換

平面變換

名稱

• 變換
  • 幾何影像變換
  • 幾何變換
  • 座標變換
• 投影
  • 製圖地圖投影（在 3D 到 2D 圖形的情況下）
• 對映

理論

2D 光柵圖形中的對映是一個複雜的函式 $f$，它將複平面對映到複平面。

$f:\mathbb {C} \to \mathbb {C}$

它被實現為點變換。

它通常表示為

$w=f(z)$

其中

• $z=x+yi$ 是複平面的一個點（輸入）
• $w=u+vi$ 是影像複平面的一個點（輸出 = 結果）

示例程式碼

例如，墨卡託：

function Spherical_mercator(x, y) {
  return [x, Math.log(Math.tan(Math.PI / 4 + y / 2))];
}

function transverseMercatorRaw(lambda, phi) {
  return [log(tan((halfPi + phi) / 2)), -lambda];
}

transverseMercatorRaw.invert = function(x, y) {
  return [-y, 2 * atan(exp(x)) - halfPi];
};

如果有人使用離散幾何（多邊形和折線），那麼投影就很難實現。必須在精度和效能之間取得平衡。

// https://github.com/adammaj1/Mandelbrot-Sets-Alternate-Parameter-Planes/blob/main/src/lcm/d.c
// projection from p to c 
complex double map_parameter(const ParameterTypeT ParameterType, const complex double parameter){

	
	complex double p; 
	// plane transformation 
	switch(ParameterType){
	
		case c_identity :{p = parameter;  break;}
		
		case c_inverted :{p = 1.0/parameter; break;}
		
		case c_parabola :{p = 0.25+ 1.0/parameter; break;}
		
		case c_Myrberg_type :{p = cf - 1.0/parameter; break;}
		
		case c_inverted_2_type :{p = -2.0 + 1.0/parameter; break;}
		
		case c_exp :{p = cf + cexp(parameter) ; break;} // here one can change cf to get different image 
		
		
		case lambda_identity :{ p = parameter;  break;}
		
		case lambda_inverted_type :{p = 1.0/parameter; break;}
		
		case lambda_inverted_1_type :{p =1.0+ 1.0/parameter; break;}
		
		default: {p = parameter;}
	}

分類

對映分類

• 基於物件的對映（影像物件是具有相同整數值的連線畫素集）
• 基於畫素的對映

2D 圖形中的變換（對映）

• 基本型別
• 複合變換

實現

矩陣的使用

• 不使用矩陣（使用函式）
• 使用矩陣

座標

• 使用笛卡爾座標
• 使用齊次座標

矩陣

• "矩陣乘法不滿足交換律。變換的順序至關重要——旋轉後平移與平移後旋轉截然不同"

實現

• Imath 是一個 C++ 和 python 庫，用於計算機圖形的 2D 和 3D 向量、矩陣和數學運算。

• 矩陣的部分
• 
  行
• 
  列

型別

• 縮放
• 反轉
• 展開（閉合曲線）
• 應用於圖片的共形對映
• 梅比烏斯變換
• 指數和墨卡托地圖

仿射變換

為了用矩陣表示仿射變換，我們可以使用齊次座標。這意味著將 2 向量 (x, y) 表示為 3 向量 (x, y, 1)，更高維度也是如此。

2D 仿射變換矩陣

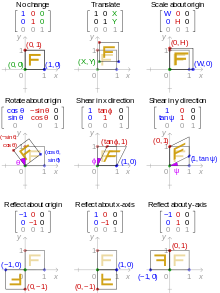
變換名稱	仿射矩陣	示例
恆等（變換到原始影像）	${\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$
平移	${\begin{bmatrix}1&0&v_{x}>0\\0&1&v_{y}=0\\0&0&1\end{bmatrix}}$
反射	${\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$
縮放	${\begin{bmatrix}c_{x}=2&0&0\\0&c_{y}=1&0\\0&0&1\end{bmatrix}}$
旋轉	${\begin{bmatrix}\cos(\theta )&-\sin(\theta )&0\\\sin(\theta )&\cos(\theta )&0\\0&0&1\end{bmatrix}}$	其中 θ = π/6 =30°
剪下	${\begin{bmatrix}1&c_{x}=0.5&0\\c_{y}=0&1&0\\0&0&1\end{bmatrix}}$

仿射變換適用於將兩幅或多幅影像對齊（配準）的配準過程。一個影像配準的例子是全景影像的生成，全景影像是多幅拼接在一起的影像的產物。

縮放或調整大小

關於原點按比例因子縮放物體

$s=s_{x}+s_{y}*i$ 

$x'=x*s_{x}$
$y'=y*s_{y}$

變為

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}s_{x}&0&0\\0&s_{y}&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}$$

縮放

• 均勻（在縮放時保持物體的比例）：sx = sy
• 非均勻：sx != sy

在保持固定中心點的情況下調整物體大小 = 關於其自身中心縮放物體

• 寬度' = 寬度 * sx
• 高度' = 高度 * sy
• 計算中心點的角座標

平移

複數平移是一個對映

$z'\to z+t$

其中

• $z=x+y*i$
• $z'=x'+y'*i$
• $t=t_{x}+t_{y}*i$

使用這種系統，平移可以用矩陣乘法表示。 函式形式

$x'=x+t_{x}$ 
$y'=y+t_{y}$ 

變為

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}1&0&t_{x}\\0&1&t_{y}\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}.$$

旋轉

繞原點以角度 θ 逆時針（正方向）旋轉的函式形式為

$x'=x\cos \theta -y\sin \theta$ 
$y'=x\sin \theta +y\cos \theta$.  

寫成矩陣形式，就變成了：

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}$$

類似地，繞原點順時針（負方向）旋轉的函式形式為

$x'=x\cos \theta +y\sin \theta$ 
$y'=-x\sin \theta +y\cos \theta$ 

矩陣形式為

$${\begin{bmatrix}x'\\y'\\1\end{bmatrix}}={\begin{bmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}x\\y\\1\end{bmatrix}}$$

這些公式假設x軸指向右側，y軸指向上方。

歸一化座標下的逆時針旋轉矩陣

$${\begin{bmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}$$

沒有矩陣的 C 程式碼

 
/* 

C program to rotate an object by a given angle about a given point
gcc r.c -Wall -Wextra -lm
./a.out
*/

#include <stdio.h>
#include <math.h> 
#include <complex.h> 		// complex numbers : https://stackoverflow.com/questions/6418807/how-to-work-with-complex-numbers-in-c


//The sin() function returns the value in the range of [-1, 1]

/*
https://stackoverflow.com/questions/2259476/rotating-a-point-about-another-point-2d 
First subtract the pivot point (cx,cy), then rotate it (counter clock-wise), then add the point again.
*/


 complex double rotate_point(const complex double center, const double angle_in_radians, const complex double point )
{
	// translate point to center
	complex double translated_point = creal(point) - creal(center)  + (cimag(point) - cimag(center))*I;

	// rotate point counter clock-wise by a given angle about a given pivot point ( center)
	double s = sin(angle_in_radians);
	double c = cos(angle_in_radians);
	complex double new_point = creal(translated_point) * c - cimag(translated_point) * s + (creal(translated_point) * s + cimag(translated_point) * c)*I;

	// translate point back
	new_point = creal(new_point) + creal(center) +(cimag(new_point) + cimag(center))*I;
  
  
	return new_point;
}

#define kMax 6

// center, angle_rad, point 
double examples[kMax][5] = {
		{50,-50, -0.7853982, 100,100 },
		{50,-50, -0.7853982, 100,200 },
		{50,-50, -0.7853982, 200,200 },
		{0,0, 1.570796, 100,100}, 
		{0,0, 1.570796, 150,200}, 
		{0,0, 1.570796, 200,200} 

};

int main(void){

	
	
	
	int k;
	
	
	
	complex double center ;
	double angle_r ; 
	complex double point ;
	complex double rotated_point;
	
	
	for (k=0; k<kMax; ++k){
		center = examples[k][0] + examples[k][1] * I ;
		angle_r = examples[k][2]; 
		point = examples[k][3] + examples[k][4] * I ;
		rotated_point = rotate_point(center, angle_r, point );
		fprintf(stdout, "point %f%+f*I rotated about %f%+f*I  by %f radians is %f%+f*I \n", creal(point), cimag(point), creal(center), cimag(center), angle_r, creal(rotated_point), cimag(rotated_point));
		}
	
	 


	return 0;
}

輸出

point 100.000000+100.000000*I rotated about 50.000000-50.000000*I  by -0.785398 radians is 191.421359+20.710673*I 
point 100.000000+200.000000*I rotated about 50.000000-50.000000*I  by -0.785398 radians is 262.132040+91.421348*I 
point 200.000000+200.000000*I rotated about 50.000000-50.000000*I  by -0.785398 radians is 332.842715+20.710668*I 
point 100.000000+100.000000*I rotated about 0.000000+0.000000*I  by 1.570796 radians is -99.999967+100.000033*I 
point 150.000000+200.000000*I rotated about 0.000000+0.000000*I  by 1.570796 radians is -199.999951+150.000065*I 
point 200.000000+200.000000*I rotated about 0.000000+0.000000*I  by 1.570796 radians is -199.999935+200.000065*I 

其他有趣的對映

• 
• 
• 
• 
  帶有 python 程式碼
• 
• 
• 
• 
• 

例子：

• Jason Davies：地圖
• 桶形失真
• 螺旋形
• 對數極座標圖
• 拋物柱面座標
• 拋物線座標
• 共形對映的數值近似
• 描述
• 拐點
• Altmetric：25次引用：1更多詳細資訊文章 | 開放量子物理中的指數敏感性及其成本，作者：András Gilyén、Tamás Kiss 和 Igor Jex
• 布拉施克乘積
• 化圓為方
• 橢圓，作者：Claude Heiland-Allen
• 作者：Paul Bourke
• 製圖投影是二維中的非線性變換
  • 地圖投影和座標變換
• 到球體
• 曼德爾布羅特集合投影到收縮的黎曼球體上，作者：Arneauxtje
• 曼德爾布羅特象谷（短版本）蒂莫西·蔡斯
• 曼德爾布羅特芽和分支蒂莫西·蔡斯蒂莫西·蔡斯
• craftvid 製作的曼德爾布羅特集合球體縮放影片  : "這是曼德爾布羅特集合的 300 萬億倍縮放。 影像設定在球形“莫比烏斯”投影上，旨在包裹到球形表面上。 影像在球體的正面中心放大，同時在球體的背面逐漸消失。"
• 貓眼 : 反轉的曼德爾布羅特集合，作者：denis archambaud
• 反轉和冪曼德爾布羅特集合，作者：Jens-Peter Christensen
• Z² + Sin(Cˉᵐ+phase)，作者：Jens-Peter Christensen
• snibgo 的 ImageMagick 頁面：桶形和針墊形
• snibgo 的 ImageMagick 頁面：3D 縮放、旋轉和平移 請參閱立方體地球

共形對映

• "共形對映保持角度，並將無窮小圓對映到無窮小圓。 非共形對映將無窮小圓對映到無窮小橢圓（或更糟）。" Claude Heiland-Allen
• "複函式 $f(z)$ 在無窮遠處是共形的，如果函式 $f(1/z)$ 在 0 處是共形的。 這等同於通常的關於共形的定義，即在大小和方向（順時針/逆時針）方面保持角度不變，如果你將 $f$ 視為在黎曼球體的“北極”處保持角度不變。"

• 共形冪
• 
• 
• 
• 
• 
• 
• 

• 

共形對映

• henry seg：python 中的球形影像編輯
• newconformist：將雙曲平面共形對映到任意形狀，作者：Zeno Rogue
• 應用於圖片的共形對映示例
• 梅比烏斯變換
• 共形幾何處理概述（2017 年），作者：Keenan Crane
• 離散共形變形：演算法與實驗，作者：Jian Sun、Tianqi Wu、Xianfeng Gu 和 Feng Luo
• 共形對映
• 龐加萊雙曲圓盤共形對映食譜，作者：bugman123
• 用 Python 視覺化共形對映，作者：MJ Gruber
• 共形動畫，作者：denis archambaud
• ConformalMaps 是一個 Julia 包，用於將來自簡單連通平面域到圓盤的黎曼對映進行近似。 它使用拉鍊演算法，如 Don Marshall 和 Steffen Rohde 的論文《共形對映拉鍊演算法的收斂性》中所述。
• sswatson：ConformalMaps

共形對映詞典，作者：John H. Mathews 和 Russell W. Howell（2008 年）

• 第 1 部分
• 第 2 部分
• 第 3 部分
• 第 4 部分

製圖地圖投影

圓柱投影

球體到圓柱的正切（赤道）投影的幾何形狀。

圓柱投影（或圓柱 p.）將球體（無極點）對映到圓柱上

茹科夫斯基變換（對映）

描述 

• John D Cook

域著色或復相圖

複雜函式的視覺化

• 視覺化複雜函式的 5 種方法
• commons : Category:Complex_functions
• Rand Asswad 的複雜對映
• Paul Nylander 的龐加萊雙曲圓盤共形對映配方
• david lowry-duda : phase_mag_plot/

模形式

• David Lowry-Duda 的模形式
• L 函式和模形式資料庫 (LMFDB)

黎曼對映

• Christopher J. Bishop 的黎曼對映定理
• ©2015 LYM Canada 的針對反傻瓜的黎曼對映
• 對映元件到單位圓盤 (黎曼對映)
  • 乘子對映 和內部射線
    • 在引數平面上
    • 在動力平面上
  • Boettcher 對映、復勢和外部射線
    • 在引數平面上
      • 引數射線 = 場線
      • 復勢、外部角度

參考文獻

• J. Ström、K. Åström 和 T. Akenine-Möller 的沉浸式線性代數