消歧義

平面的指數對映是

是平面的指數變換

平面的指數對映不是

指數函式（指數對映）的茱莉亞集合或曼德博集合，例如指數曼德博集合 z := exp(z) + c
一個軸上的對數刻度^[1]
兩個軸上的對數刻度：對數-對數刻度圖^[2]
極方位等距投影（黎曼幾何中的指數對映）^[3]
指數運算元，可以應用於灰度影像的變形運算元。^[4]

比較不同輸入下的指數函式

單個數字（0D 空間）給出數字的自然指數
數軸（1D 空間）。指數刻度不用。對數刻度用於指數資料。它給出線性函式。^[5]
平面（2D 空間）給出指數對映

數字

在數學中，對數是指數運算的逆函式。這意味著以 b 為底的數字 x 的對數是指將 b 提高到該指數，以產生 x

y=\log _{b}x

等同於

x=b^{y}

如果 $b$ 是一個正實數。（如果 $b$ 不是一個正實數，則指數和對數都可以定義，但可能取多個值，這使得定義變得更加複雜。）^[6]

對數函式和指數函式
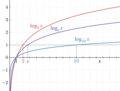
對數函式的圖，具有三個常用的底數。特殊點 $log b b = 1$ 由虛線表示，所有曲線在 $log b 1 = 0$ 交匯
以 2 為底的對數圖在x軸處交於 $x = 1$ ，並透過點 (2, 1)，(4, 2) 和 (8, 3)，例如， $log 2 (8) = 3$ 和 $23 = 8$ 。該圖無限接近於y軸，但不會與之相交

實指數函式是從 $\mathbb {R}$ 到 $(0;\infty )$ 的雙射。^[7] 它的逆函式是自然對數，記作 $\ln ,\log ,\log _{e};$ ；因此，一些舊的文字將指數函式稱為反對數。

尺度

對數刻度（或對數刻度）是一種以緊湊的方式顯示數值資料跨越非常大範圍的值的方法——通常資料中最大的數字比最小的數字大數百甚至數千倍。這種刻度是非線性的：在對數刻度上，數字 10 和 20 以及 60 和 70 之間的距離並不相同。相反，數字 10 和 100 以及 60 和 600 的間距是相等的。因此，沿著刻度移動一個單位距離意味著該數字已乘以 10（或其他固定因子）。通常，指數增長曲線會顯示在對數刻度上，否則它們會增長得太快，無法容納在小型圖表中。另一種思考方式是資料的位數以恆定的速度增長。例如，數字 10、100、1000 和 10000 在對數刻度上是等距的，因為它們的位數每次增加 1：2、3、4 和 5 位。這樣，增加兩位數會使對數刻度上測量的量乘以 100。

對數刻度

在 1 個軸上 = 半對數圖^[8]
- 線性-對數圖
- 對數-線性圖
在兩個軸上 = 對數-對數圖^[9]

Lin-Lin 刻度
Log-Lin 刻度
Lin-Log 刻度
Log-Log 刻度

對數刻度用於指數資料。它給出線性函式。^[10]^[11]

對映

道格拉斯·N·阿諾德的複變函式圖形:
- "復指數函式將以正負πi為界的無限開帶一一對映到平面減去負實軸。
- 實部為常數的直線對映到圓，而虛部為常數的直線對映到從原點出發的射線。
- 在動畫中，我們檢視的是帶內的一個矩形，而不是整個帶，因此覆蓋的區域是一個環減去負實軸。
- 環的內邊界非常靠近原點，幾乎不可見。
- 我們還使帶的寬度略小於2π，以便環不會完全閉合."
- 復指數函式將矩形|Re(z)| ≤ a，|Im(z)| ≤ π對映到環 $e^{-a}\leq |w|\leq e^{a}$
保羅·福爾斯特德的複變函式組合檢視器 - 選擇的對映函式的組合：g(f(z))。需要增加網格大小才能獲得相同的效果（矩形到環的對映）。
復指數函式作者：蘇珊·阿丁頓
複變函式對映作者：胡安·卡洛斯·龐塞·坎普薩諾
復指數函式作者：濱田達吉 : 復指數函式將矩形域對映到扇形影像（穿孔圓的部分或完整扇區）
復指數對映由 Siamak 在 GeoGebra 上繪製:
- 垂直軸被變換到 w 平面的圓上
- 水平軸被變換到 w 平面的半徑上
(保角)指數對映下 [-3,3]x[-3,3] 大小的正方形網格的影像幾乎是完整的環^[12]
復指數函式將矩形 [-1,1]x[0 ,pi/2] 雙全純對映到四分之一環 $[e^{-1},e]x[e^{-1},e]$ ^[13]
太平洋科技的復指數函式 24 個檢視
Mathematica 問題：如何將 expz 作為復變對映視覺化

虛擬數學博物館：保角對映，復指數函式"笛卡爾網格被“保角地”對映到極座標網格（即保持角度）：實軸的平行線被對映到徑向線，而平行於虛軸的長度為 2π 的線段被對映到以 0 為中心的圓."

exp(x + i · y) = exp(x) · exp(i · y) = exp(x) · cos(y) + i · exp(x) · sin(y)

表示復指數的曲面
實部
虛部
模量 = cabs
主幅角 = carg

表示復指數的密度曲線
實部
虛部

指數對映
對數極座標對映。點 (x,y) 被對映到 $(\rho ,\theta )$ 其中 $\rho =\log {\sqrt {x^{2}+y^{2}}}$ 和 $\theta =\arctan({\frac {y}{x}})$ 。一般來說，以原點為圓心，半徑為 r 的圓被對映到水平線和垂直線。
墨卡託投影與旋轉
從切空間到球體的指數對映

3D	2D	描述
$f(z)=\exp(z)$	$f(z)=\exp(z)$
$f(z)=\log(z)$	$f(z)=\log(z)$

週期

指數函式是週期性的

exp(z + 2 π * i) = exp(z).

從公式中也可以清楚地看出週期性

exp(x + i * y) = exp(x) * (cos(y) + i * sin(y)) .

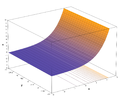
指數函式的圖形是一個二維曲面 (x,y)，它在四維空間 (x,y,v,w) 中彎曲。

v+iw = exp(x+iy) 對於從 -1.5 到 1.5 的 x 值和從 -2π 到 2π 的 y 值，因此顯示了螺旋的兩個完整旋轉。

名稱

指數對映^[14]
指數對映^[15]^[16]^[17]
墨卡託（這不是一個好的名字，因為這裡只是從平面複平面（二維笛卡爾平面）到指數平面的對映。這裡沒有從球面到平面複平面（笛卡爾平面）的對映^[18]）
- 墨卡托地圖
- 墨卡託投影^[19]^[20]^[21]^[22]
極座標投影
對數極座標對映（對數極座標）
對數^[23]
- 以點 c0 為中心的對數投影：z-> (log(|z-c0|)
log(z)-Mandelbrot-Zooms^[24] = 側滾（側滾分形縮放）^[25]^[26]^[27]

一般名稱

圖形投影
幾何變換

描述

 Math notation

$map:\mathbb {C} \to \mathbb {C}$

$c_{e}\leftarrow e^{c}+c_{0}$

// c with complex type
complex double map(complex double c) {
return c_e = cexp(c) + c0; }

// c without complex type
cx_e = exp(creal(c)) * cos(cimag(c)) + realpart(c0); // real part of c_e
cy_e = exp(creal(c)) * sin(cimag(c)) + imagpart(c0); // imag part of c_e

特點

對映

笛卡爾平面上的矩形到極座標的二次扇區，
x 對映到半徑，y 對映到角度（弧度）^[28]

水平方向
- 對映 $c_{0}$ 到無窮大（序列的極限 = MF = Myrberg-Feigenbaum 點 = Feigenbaum 點)
- 將與上述序列相關的關鍵元件對映到相同大小
垂直方向
- 垂直座標是以 $2\pi$ 為週期的，因為它們使用了三角函式

例子

週期為 $p=1*2^{n}$ （週期倍增級聯）的根點序列，並且該序列的極限點是 Myrberg-Feigenbaum 點 $\mathbf {MF} _{1/2}=c_{0}=-1.401155...$
週期為 $p=1*3^{n}$ 的根點序列，並且該序列的極限點是 Myrberg-Feigenbaum 點 $\mathbf {MF} =c_{0}=-1.7864402555636388747...$

非正式描述

指數對映將整個複平面轉換為一個條帶，該條帶沿實軸無限延伸，沿虛軸的寬度為 2π。指數對映來自曼德爾布羅集詞彙表和百科全書，作者羅伯特·穆納福，(c) 1987-2022
" 其思想是專注於曼德爾布羅集內或附近的某個點，並建立一個影像，其中一個方向是距離的對數，另一個方向是角度。結果非常類似於 astro-ph/031571 地圖^[29] 和 XKCD 漫畫版本。^[30] 該地圖投影是共形的，因此它不會扭曲區域性角度，並且物體通常在所有尺度上都是可識別的。" 安德斯·桑德伯格^[31]
曼德爾布羅集的影像，以 c0 為中心，採用對數投影：z-> (log(|z-c0|), arg(z-c0))。安德斯·桑德伯格 ^[32]
" 它是一個朝向目標點的對數對映（或者，正如有些人可能說的那樣，一個以目標點為南極、複數 ∞ 為北極的墨卡託投影）；水平方向是週期性的，我將兩個週期並排放置，而垂直方向則在頂部和底部延伸到無窮大，這對應於無限地放大或縮小，每次一個水平週期的尺寸為 exp(2π)≈535.5。對數對映上的水平線（“平行線”）對應於目標點的同心圓，垂直線對應於從目標點發出的半徑；並且變形保持角度。" 戴維·馬多爾 ^[33]
" 座標系使得角度分量對映到結果影像的 y 軸，半徑對映到 x 軸。此外，x 軸（半徑）使用 exp 函式進行歸一化，以便在該對映中保留角度。 " 米卡·塞帕 ^[34]
log : " 為了說明曼德爾布羅集邊界的複雜性，圖 8 顯示了 dM 在變換 log(z - c) 下的影像，其中 c 為曼德爾布羅集邊界的某個點。請注意，主心形的上右側有一個尖點；在圖中向左看對應於向點 c 放大。（具體來說，c = -0.39054087... - 0.58678790i...，該點位於主心形邊界上，對應於黃金分割西格爾圓盤。）請注意，主心形的上右側有一個尖點；在圖中向左看對應於向點 c 放大。" ^[35]
" 傳奇的橫向滾動分形縮放。1 個月+（插值器+影片編輯器）= Log(z)。這意味著該位置的對數投影，這產生了這個有趣的橫向滾動平面 ^^)" ^[36]
" 沒有程式可以在 Log(Z) 平面渲染此分形。但你可以在 Ultra Fractal 或類似的具有可程式設計分散式的軟體中製作它。公式為：C = exp(D)，其中 D 是你的可縮放座標" SeryZone X
只是 c = c0 + cexp(x + i y) 和 x + i y = clog(c - c0)，以 2pi/width 縮放（克勞德）
想法
- J. Richard Gott III、Mario Jurić、David Schlegel、Fiona Hoyle、Michael Vogeley、Max Tegmark、Neta Bahcall、Jon Brinkmann 編著的《宇宙地圖》
- XKCD 漫畫版本

正式數學描述

正向變換

這裡變換是 2 個變換的合成

復指數函式: $f(c)=e^{c}$
幾何或複數平移 $t(x)=x+c_{0}$

  $c_{e}=t(f(c))$

c_{e}\leftarrow e^{c}+c_{0}

其中

c 是 c 平面（笛卡爾座標系中的平面圖像 = 兩個軸上的線性刻度）中的一個引數點。它是二次對映 $z^{2}+c$ 的一個引數
$c_{e}$ 是新變換平面（對數極座標影像）中的一個引數
$c_{0}$ 是一個常數引數（用於平移）。有時稱為中心，但更好的名稱似乎是：目標或極限點
e 是尤拉數，是一個數學常數，約等於 2.71828，

逆變換:

c=ln(c_{e}-c_{0})

其中

$ln$ 是自然對數

exp

復指數對映

復指數函式是週期性的，週期為 $2 πi$ ，並且 $\exp(z+2\pi ik)=\exp z$ 對所有 $z\in \mathbb {C} ,k\in \mathbb {Z}$ 成立。

指數函式將複平面中的任何直線對映到複平面中的對數螺旋線，中心位於原點。存在兩種特殊情況

當原直線平行於實軸時，生成的螺旋線永遠不會閉合自身；
當原直線平行於虛軸時，生成的螺旋線是某個半徑的圓。

將復指數函式視為涉及四個實變數的函式： $v+iw=\exp(x+iy)$ 指數函式的圖形是一個在四個維度上彎曲的二維曲面。

從 $xy$ 域的彩色編碼部分開始，以下是該圖形的不同投影到二維或三維空間中的表示。

復指數函式的圖形
棋盤格鍵
$x>0:\;{\text{green}}$
投影到範圍複平面 (V/W)。與下一個透檢視像進行比較。
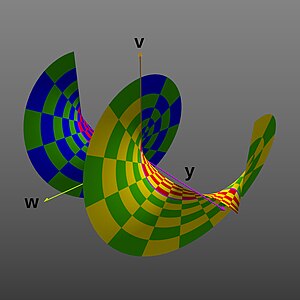
投影到 $x$ 、 $v$ 和 $w$ 維度，產生一個喇叭狀或漏斗狀的形狀（想象成二維透檢視像）。
投影到 $y$ 、 $v$ 和 $w$ 維度，產生螺旋形狀。 ( $y$ 範圍擴充套件到 $\pm 2\pi$ ，再次作為二維透檢視像）。

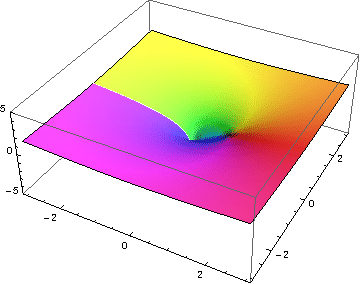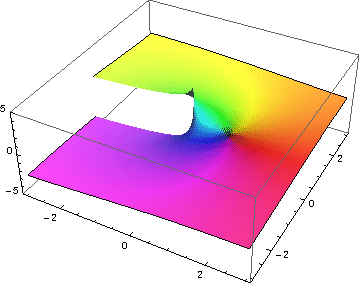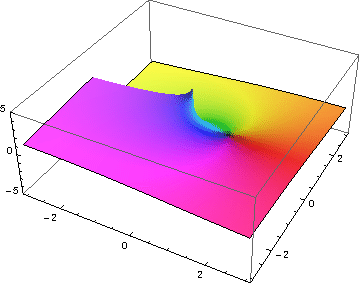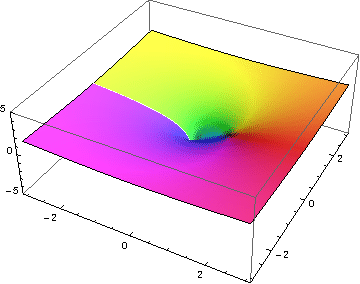
第二張圖展示瞭如何將域複平面對映到值域複平面。

零對映到 1
實數 $x$ 軸對映到正實數 $v$ 軸。
虛數 $y$ 軸以恆定角速度繞單位圓旋轉。
具有負實部的值對映到單位圓內部。
具有正實部的值對映到單位圓外部。
具有恆定實部的值對映到以零為中心的圓。
具有恆定虛部的值對映到從零延伸的射線。

第三張圖和第四張圖展示了第二張圖中的圖形如何在其他兩個維度（在第二張圖中未顯示）上延伸。

第三張圖展示了沿實數 $x$ 軸延伸的圖形。它展示了圖形是關於實數指數函式圖形的 $x$ 軸的旋轉曲面，產生喇叭或漏斗形狀。

第四張圖展示了沿虛數 $y$ 軸延伸的圖形。它展示了圖形的曲面對於正負 $y$ 值並不真正沿負實數 $v$ 軸交匯，而是圍繞 $y$ 軸形成螺旋曲面。由於它的 $y$ 值已擴充套件到 $\pm2 π$ ，此圖也更好地描繪了虛數 $y$ 值中的 2π 週期性。

Log

複數對數作為共形對映^[37]

由於 ** $\log z$ ** 的一個分支是全純的，並且由於它的導數 ** $\log z$ ** 從未為 0，它定義了一個共形對映。

例如，**主分支** $w=\operatorname {Log} z$ ，被視為從 $\mathbb {C} -\mathbb {R} _{\leq 0}$ 到由 $\left|\operatorname {Im} z\right|<\pi$ 定義的水平帶的對映，具有以下屬性，這些屬性是極座標形式公式的直接結果。

以 0 為中心的 _z_ 平面上的圓形對映到 _w_ 平面上的垂直線段，連線 $a-\pi i$ 到 $a+\pi i$ ，其中 _ $a$ _ 是圓形的半徑的對數。
從 _z_ 平面上的 0 發出的射線對映到 _w_ 平面上的水平線。

如上，_z_ 平面上的每個圓形和射線在直角處相遇。它們的 Log 對映影像是 _w_ 平面上的垂直線段和水平線（分別），它們也以直角相遇。這是 Log 的共形特性的說明。

程式設計師說明

// https://code.mathr.co.uk/mandelbrot-graphics/blob/HEAD:/c/lib/m_d_transform.c
static void m_d_transform_exponential_forward(void *userdata, double _Complex *c, double _Complex *dc) {
  m_d_transform_exponential_t *t = userdata;
  double _Complex c0 = *c;
  double _Complex dc0 = *dc;
  *c = cexp(c0) + t->center;
  *dc = dc0 * cexp(c0);
}


static void m_d_transform_exponential_reverse(void *userdata, double _Complex *c, double _Complex *dc) {
  m_d_transform_exponential_t *t = userdata;
  double _Complex c0 = *c;
  double _Complex dc0 = *dc;
  *c = clog(c0 - t->center);
  *dc = dc0 / (c0 - t->center);
}

從 MathMap 過濾墨卡託

filter mercator (image in)
   in(xy*xy:[cos(pi/2/Y*y),1])
end

Maxima CAS 原始碼

(%i1) kill(all);
(%i2) display2d:false;
(%i3) ratprint : false; /* remove "rat :replaced " */
(%i4) c:cx +cy*%i$
(%i5) c0:c0x+c0y*%i$
(%i6) realpart(c0 + exp(c));
(%o6) %e^cx*cos(cy)+c0x
(%i7) imagpart(c0 + exp(c));
(%o7) %e^cx*sin(cy)+c0y
(%i8) cabs(c0 + exp(c));
(%o8) sqrt((%e^cx*sin(cy)+c0y)^2+(%e^cx*cos(cy)+c0x)^2)
(%i9) carg(c0 + exp(c));
(%o9) atan2(%e^cx*sin(cy)+c0y,%e^cx*cos(cy)+c0x)

筆記

該對映是**週期性的**，因為內部有三角函式。

(%i1) kill(all);
(%i2) display2d:false;
(%i3) ratprint : false; /* remove "rat :replaced " */
(%i4) ce:ceex+cey*%i;
(%i5) c0:c0x+c0y*%i;
(%i6) realpart(log(ce - c0));
(%o6) log((cey-c0y)^2+(ceex-c0x)^2)/2
(%i7) imagpart(log(ce - c0));
(%o7) atan2(cey-c0y,ceex-c0x)

// https://www.foerstemann.name/dokuwiki/doku.php?id=log_z_-mandelbrot-zooms
// log(z)-Mandelbrot-Zooms by 
<languageVersion: 1.0;> 
kernel zoomer
< namespace : "Zoomer"; vendor : "private"; version : 2; description : "zoomer 2"; >
{
  const float PI = 3.14159265;
  const float EU = 2.71828; 
  parameter float translate <       
      minValue:float(0);
      maxValue:float(400.0); 
      defaultValue:float(0.0); >;
  parameter float rotate <       
      minValue:float(0.0);
      maxValue:float(960.0); 
      defaultValue:float(0.0); >;
  input image4 iImage1;
  input image4 iImage2;
  input image4 iImage3;
  input image4 iImage4;
  output float4 outputColor;
  void evaluatePixel()
  {
      float2 position = outCoord() - float2(479.5,199.5);
      float2 tmp = outCoord();
      tmp.y = abs(log(sqrt(pow(position.x,2.0) + pow(position.y,2.0))/510.0))*30.474;
      tmp.x = mod((atan(position.x, position.y)/PI + 1.0)*480.0, 958.5) ;
      position = tmp + float2(rotate,translate);
      position.x = mod(position.x,958.5)+1.0;
      if ( position.y < 398.5) {outputColor = sampleLinear( iImage1, position );} 
      else if ( position.y < 797.0) {outputColor = sampleLinear( iImage2, position - float2( 0.0 , 398.0 ));} 
      else if ( position.y < 1199.5) {outputColor = sampleLinear( iImage3, position - float2( 0.0 , 796.0 ));}
      else {outputColor = sampleLinear( iImage4, position - float2( 0.0 , 1194.0 ) );}  
  }
}

中心

$c_{0}$ 是一個常數引數（用於平移 = 偏移）。

它有時被稱為中心，但更好的名稱似乎是

目標
極限點
偏移或平移

目標點（中心）被投影到指數對映檢視中的 -∞+0i。它將在最左邊無限遠，並且在影像上不可見。

縮放

影像的最左列具有最小縮放（最大的平面半徑）
影像的最右列具有最大縮放（最小的平面半徑）

指數網格掃描

約定

Robert Munafo 基於水平畫素座標生成角度，並基於垂直畫素座標生成半徑（影像處於垂直位置，它位於較短的尺寸上）
通常的方法是從垂直畫素座標獲得角度（影像處於水平位置，它位於較長的尺寸上）

具有指數座標對映的網格掃描與平面圖像的標準掃描不同。

for (int j = 0; j < h; ++j) { // vertical coordinate = number of the rows
    
     double e_angle = ((double) j) * px / r * 3.14159265359;  // Robert's way:  angle from 0 to 2π. 
   
   for (int i = 0; i < w; ++i) { // horizontal coordinate = number of the columns
    
       e_radius = ((double) i) * px / r * 3.14159265359;
       .....
    }

描述

影像寬度是最大畫素數 = 影像以畫素為單位的寬度（整數）

這裡

畫素座標 j 從 0 到影像高度 - 1
因此 j/畫素高度從 0.0 到 1.0
因此角度從 0 到 2 pi

Claude 的方法在數學上是正確的：角度通常被認為是從 -π 到 π，而不是從 0 到 2π。要解決這個問題，您可以在從其計算角度之前調整畫素座標。更改此

double e_angle = ((double) j) * px / r * 3.14159265359;

為此

double e_angle = ((double) (j-h/2)) * px / r * 3.14159265359;

筆記

e_radius 是 i 的線性函式
e_angle 是 j 的線性函式

計算畫素座標

以下是由 Robert Munafo 提供的示例^[39]

   /* Inputs are:
     ctr_r is the real coordinate of the center of the view we want to plot
     ctr_i is the imaginary coordinate of the center of the view
     
     real_width is the width of the image (in real coordinates). this should reflect the width when "zoomed in" all the way
     
     pixel_width is the number of pixels per row of the image we want to create
     pixel_height is the number of rows of pixels, or pixels per column
  
     This setup code computes:
     px_spacing is the width of the image (in real coordinate)
       divided by the number of pixels in a row
     halfwidth is half the width of the image (in real coordinate)
     halfheight is half the height of the image (in imaginary coordinate)
     min_r is the real coordinate of the left edge of the image
     max_i is the imaginary coordinate of the top of the image
  */
  void setup()
  {
    px_spacing = real_width / pixel_width;
    halfwidth = real_width / 2.0;    
    halfheight = halfwidth * pixel_height / pixel_width;
    min_r = ctr_r - halfwidth;
    max_i = ctr_i + halfheight;
  }
  

  /* Plot a single pixel, row i and column j. Use as many rows as you need
     for the image to show the whole Mandelbrot set. */
  void pixel_53(int i, int j, int itmax)
  {
    double cr, ci, offset_r, offset_i, angle, log_radius;
  
    /* compute angle and radius. Note that pixel_width is the number of
       pixels wide of the image, and j goes from 0 to pixel_width-1. This
       means that "j/pixel_width" goes from 0.0 to 1.0, and therefore
       angle goes from 0 to 2 pi. log_radius needs to be computed the
       same way in order for shapes to be preserved, which happens because
       the complex exponential function is a conformal map.
    Important: the row coordinate i can be as big as you want: add as many
       rows of pixels as are needed for the "log_radius" to get close to 1.
       This ensures that exp(log_radius) gets big enough to go beyond the
       area that has the Mandelbrot set in it. */
    angle =      (((double) j) / pixel_width) * 2.0 * 3.14159265359;
    log_radius = (((double) i) / pixel_width) * 2.0 * 3.14159265359;
  
    /* compute offsets = translation = add complex number offset */
    offset_r = cos(angle) * halfwidth * exp(log_radius);
    offset_i = sin(angle) * halfwidth * exp(log_radius);
  
    ci = ctr_i + offset_i;
    cr = ctr_r + offset_r;
    evaluate_and_plot(cr, ci, itmax, i, j);
  }

與

Claude Heiland-Allen 的指數條帶進行比較：最終影片的渲染可以透過在重新投影到一系列平面圖像之前，圍繞縮放中心計算指數間隔的環來加速。如果出現問題，請訪問：https://mathr.co.uk/mandelbrot/exponential_strip.svg

縱橫比

為了獲得最佳（更共形）結果，請使用寬縱橫比（9:1 效果很好，視窗大小為 1152x128 或 1536x170）。

比例因子 R

為了最大程度地減少需要計算的畫素總數，這與^[40]成正比

 $K={\frac {R^{2}-1}{logR}}$

用以下公式定義縮放效率：

 ${\frac {2}{K}}$

那麼

傳統的 R=2 的效率只有 46%，
R=4/3 的效率為 74%
R=8/7 的效率為 87%

其中

影片影像大小為 W×H

影片

影像

類別：曼德勃羅特集合 - commons 中的墨卡託投影

無變換
實數（= 1D）版本
1D：3 個具有非線性（即對數）x 軸比例的視窗
複數（= 2D）版本
正投影
極座標投影
M(3,1) Misiurewicz 在 1E10 倍放大率下（底部）使用指數對映
GIMP 中的墨卡託效果，使用 MathMap

兩張具有相同引數的影像。在上圖中，主天線位於兩側，在下圖中位於影像的中心

墨卡託
靠近 Myrberg-Feigenbaum 點區域的對映圖。主曼德勃羅特集合的芽以幾何方式收斂到該點（以 Feigenbaum 常數設定的速率），在頂部和底部產生規律間隔的芽。由於我沒有它的精確座標，因此該地圖的中心略微偏離。
此影像對應於圍繞一個點的 10^30 倍縮放（我只使用了 30 位精度，因此左側邊緣存在偽影
此影像對應於圍繞一個點的 10^30 倍縮放（我只使用了 30 位精度，因此左側邊緣存在偽影）。
10^60 倍縮放。條帶結構的出現是因為縮放穿過圍繞較小曼德勃羅特集合的嵌入朱利亞集合；每個經過縮放的新曼德勃羅特集合都會將其自己的朱利亞集合新增到序列中。中心點為 c=-1.256827152259138864846434197797294538253477389787308085590211144291 +0.37933802890364143684096784819544060002129071484943239316486643285025i
$Zooms of the Mandelbrot set around a point projected so that the distance to the point forms a logarithmic scale. Details on the left edge are ~10^15 times smaller than on the right edge. The rightmost black blob in the pictures is the main "continent" of the set. Satelite sets of different sizes can be seen linked by fractal chains of varying complexity. The colors are set using the distance estimator method.$

曼德勃羅集在某一點周圍的縮放，投影方式使該點距離形成對數刻度。左邊緣的細節比右邊緣小約 10^15 倍。圖片中最右邊的黑色斑點是集合的主要“大陸”。不同大小的衛星集可以透過不同複雜程度的分形鏈連線起來。顏色使用距離估計器方法設定。

如何從指數影像中讀取位置？

fractalforums.org : 你能找到這個分形的位置嗎？
"使用複數對數函式進行逆對映（將計算所需資料的在條帶中的位置，以正常正交座標空間中的給定位置表示）" Robert Munafo^[41]

提示

影像不具有對稱性（上下），因此 c0 的虛部不為零

實現

分形程式

fraktaler-3
UltraFractal
fractalzoomer 中的 Polar_Projection
Fractalshades - Geoffroy Billotey 編寫的 Python 程式
emndl: 曼德勃羅集的指數條帶視覺化，Claude Heiland-Allen 編寫的程式
pfract - Mika Seppä 編寫的控制檯 C 程式
emndl: mathr 的指數條帶曼德勃羅集渲染器: 它為: c = c0 + cexp(x + i y) 並且 x + i y = clog(c - c0)，寬度縮放 2pi/width
Fractalshades 文件 : P01-feigenbaum expmap

Kalles Fractaler 和 zoomasm

最終影片的渲染可以透過在重新投影到一系列平面圖像之前，計算圍繞縮放中心的指數間隔環來加速。
kf-2.15 支援以指數對映形式渲染 EXR 關鍵幀
zoomasm 可以將以上關鍵幀組裝成縮放影片。zoomasm 從 EXR 開始，包括原始迭代資料，並且顏色演算法可以編寫在 OpenGL 著色器原始碼片段中
Claude Heiland-Allen 編寫的 kf-extras - 具有指數對映（也稱為對數極座標或墨卡託投影）轉換器

OpenCV

ImageMagic

processing

forum.processing : how-to-change-an-image-from-x-y-coordinate-to-polar-coordinate

sci-kit

Mathworks

David Young 來自 mathworks 的對數極座標影像取樣版本 1.0.0.0 (4.33 KB)

glsl

一個典型的著色器看起來像這樣（Thorsten Förstemann 編寫的程式碼）

// https://web.archive.org/web/20210715234846/https://www.foerstemann.name/dokuwiki/doku.php?id=log_z_-mandelbrot-zooms
<languageVersion: 1.0;> 
kernel zoomer
< namespace : "Zoomer"; vendor : "private"; version : 2; description : "zoomer 2"; >
{
  const float PI = 3.14159265;
  const float EU = 2.71828; 
  parameter float translate <       
      minValue:float(0);
      maxValue:float(400.0); 
      defaultValue:float(0.0); >;
  parameter float rotate <       
      minValue:float(0.0);
      maxValue:float(960.0); 
      defaultValue:float(0.0); >;
  input image4 iImage1;
  input image4 iImage2;
  input image4 iImage3;
  input image4 iImage4;
  output float4 outputColor;
  void evaluatePixel()
  {
      float2 position = outCoord() - float2(479.5,199.5);
      float2 tmp = outCoord();
      tmp.y = abs(log(sqrt(pow(position.x,2.0) + pow(position.y,2.0))/510.0))*30.474;
      tmp.x = mod((atan(position.x, position.y)/PI + 1.0)*480.0, 958.5) ;
      position = tmp + float2(rotate,translate);
      position.x = mod(position.x,958.5)+1.0;
      if ( position.y < 398.5) {outputColor = sampleLinear( iImage1, position );} 
      else if ( position.y < 797.0) {outputColor = sampleLinear( iImage2, position - float2( 0.0 , 398.0 ));} 
      else if ( position.y < 1199.5) {outputColor = sampleLinear( iImage3, position - float2( 0.0 , 796.0 ));}
      else {outputColor = sampleLinear( iImage4, position - float2( 0.0 , 1194.0 ) );}  
  }
}

Python

stackoverflow 問題: image-information-along-a-polar-coordinate-system

這樣建立的影像也稱為

指數對映
墨卡託-曼德勃羅集對映
黎曼數球的墨卡託投影。^[42]^[43]

在以下程式示例中，計算了曼德勃羅集的對數投影，

曼德勃羅集使用 NumPy 透過複數矩陣進行計算。使用 David Madore 和 Anders Sandberg 提出的一種對數投影。這種投影使得縮放動畫的計算更加容易

對數投影允許創建極速加速的曼德勃羅集縮放動畫（另請參閱 Thorsten Förstemann 的動畫和 Claude Heiland-Allen 的座標分析 ^[44]^[45]^[46]^[47]

import numpy as np
import matplotlib.pyplot as plt

d, h = 200, 1000  # Pixeldichte (= Bildbreite) und Bildhöhe
n, r = 800, 5000  # Anzahl der Iterationen und Fluchtradius (r > 2)

x = np.linspace(0, 2, num=d+1)
y = np.linspace(0, 2 * h / d, num=h+1)

A, B = np.meshgrid(x * np.pi, y * np.pi)
C = 4.0 * np.exp((A + B * 1j) * 1j) + (- 1.748764520194788535 + 3e-13 * 1j)

Z, dZ = np.zeros_like(C), np.zeros_like(C)
D = np.zeros(C.shape)

for k in range(n):
    M = Z.real ** 2 + Z.imag ** 2 < r ** 2
    Z[M], dZ[M] = Z[M] ** 2 + C[M], 2 * Z[M] * dZ[M] + 1

N = abs(Z) > 2  # Distanzschätzung des Außenbereichs
D[N] = np.log(abs(Z[N])) * abs(Z[N]) / abs(dZ[N])

plt.imshow(D.T ** 0.05, cmap=plt.cm.nipy_spectral, origin="lower")
plt.savefig("Mercator_Mandelbrot_map.png", dpi=200)