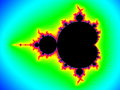
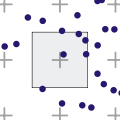
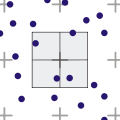
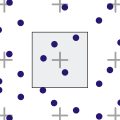
分形/掃描
掃描,取樣
取樣
- 從函式、對映、影像中獲取有限數量的值的過程。[1][2]
- 在統計學、質量保證和調查方法學中,抽樣是從統計總體中選擇個體子集(統計樣本)以估計整個總體的特徵。統計學家試圖收集代表所討論總體的樣本。抽樣比測量整個總體成本更低,資料收集速度更快,並且可以在無法測量整個總體的情況下提供見解。
分類標準:
- 遍數(單遍、多遍)
- 網格(規則=均勻/不規則或自適應)
- 隨機(隨機)/非隨機
- 有分解或無分解
按範圍劃分的取樣型別
- 點取樣=點取樣方法。種子是一個定義的、有理複雜的數字,它代表一個畫素=畫素中心。請注意,可以在一個畫素內找到無限多個點,而許多這樣的點可能具有與畫素中心不同的顏色/行為。
- 空間取樣(樣本之間發生了什麼?):一個手動定義的同質網格=均勻取樣
- 1 畫素近似=影像顯示“平面上距離填充的朱利亞集至多為畫素直徑的點的集合”[3]
按自適應劃分的取樣
- 規則、均勻(非自適應)取樣
- 自適應(非均勻)取樣=自適應網格細化 (AMR)
- 標準掃描:一步渲染整個影像(以全解析度)
- fractint 繪製方法
- 在每個後續細化步驟上進行圓形渲染
步驟
- 預覽
- 最終渲染
- 掃描標準 c 平面
- 掃描指數平面
掃描平面
- 所有畫素(平面逐畫素掃描)一次透過
- 相同的畫素大小(規則、均勻網格)
它還取決於平面描述
int SetPlane(complex double center, double radius, double a_ratio){
ZxMin = creal(center) - radius*a_ratio;
ZxMax = creal(center) + radius*a_ratio; //0.75;
ZyMin = cimag(center) - radius; // inv
ZyMax = cimag(center) + radius; //0.7;
double PixelWidth = (ZxMax-ZxMin)/iWidth;
double PixelHeight = (ZyMax-ZyMin)/iHeight; // pixel_size = PixelWidth = PixelHeight
return 0;
}
這裡在Lisp
; common lisp. Here float values can be used, there is no mapping
(loop for y from -1.5 to 1.5 by 0.1 do
(loop for x from -2.5 to 0.5 by 0.05 do
(princ (code-char 42))) ; print char
(format t "~%")) ; new line
以及在C
/* c */
/* screen coordinate = coordinate of pixels */
int iX, iY,
iXmin=0, iXmax=1000,
iYmin=0, iYmax=1000,
iWidth=iXmax-iXmin+1,
iHeight=iYmax-iYmin+1;
/* world ( double) coordinate = parameter plane*/
const double ZxMin=-5;
const double ZxMax=5;
const double ZyMin=-5;
const double ZyMax=5;
/* */
double PixelWidth=(ZxMax-ZxMin)/iWidth;
double PixelHeight=(ZyMax-ZyMin)/iHeight;
double Zx, Zy, /* Z=Zx+Zy*i */
Z0x, Z0y, /* Z0 = Z0x + Z0y*i */
for(iY=0;iY<iYmax;++iY)
{ Z0y=ZyMin + iY*PixelHeight; /* mapping from screen to world; reverse Y axis */
if (fabs(Z0y)<PixelHeight/2) Z0y=0.0; /* Zy = 0 is a special value */
for(iX=0;iX<iXmax;++iX)
{ /* initial value of orbit Z0 */
Z0x=ZxMin + iX*PixelWidth;
}
}
由 Robert Munafo 完成的正常網格掃描繪圖[10]
/* Plot a single pixel, row i and column j
NOTE:
itmax is the maximum number of Mandelbrot iterations
min_r is the real coordinate of the left edge of the image
max_i is the imaginary coordinate of the top of the image
px_spacing = pixel size is the width of the image (in real coordinates) divided by the number of pixels in a row
image aspect ratio = 1:1
*/
void pixel_53(int i, int j, int itmax)
{
double cr, ci;
ci = max_i - ((double) i) * px_spacing;
cr = min_r + ((double) j) * px_spacing;
evaluate_and_plot(cr, ci, itmax, i, j);
}
// modified code using center and radius to scan the plane
int height = 720;
int width = 1280;
double dWidth;
double dRadius = 1.5;
double complex center= -0.75*I;
double complex c;
int i,j;
double width2; // = width/2.0
double height2; // = height/2.0
width2 = width /2.0;
height2 = height/2.0;
complex double coordinate(int i, int j, int width, int height, complex double center, double radius) {
double x = (i - width /2.0) / (height/2.0);
double y = (j - height/2.0) / (height/2.0);
complex double c = center + radius * (x - I * y);
return c;
}
for ( j = 0; j < height; ++j) {
for ( i = 0; i < width; ++i) {
c = coordinate(i, j, width, height, center, dRadius);
// do smth
}
}
另一個版本
int main()
{
int aa = 4;
int w = 800 * aa;
int h = 800 * aa;
#pragma omp parallel for schedule(static, 1)
for (int j = 0; j < h; ++j)
{
double y = (h/2 - (j + 0.5)) / (h/2) * r;
for (int i = 0; i < w; ++i)
{
double x = (i + 0.5 - w/2) / (h/2) * r;
double _Complex c = x + I * y;
// proceed
}
}
return 0;
}
四叉樹型別
- 區域四叉樹
- 點四叉樹
- 距離估計,由 Claude Heiland-Allen 完成的 Koebe 1/4 定理
- 由 Mandrian 完成的快速曼德布羅集四叉樹
- 由 Rico Mariani 完成的繪製曼德布羅集的 Mariani-Silver 演算法
- 來自曼德布羅集詞彙表和百科全書的 Mariani/Silver 演算法,由 Robert Munafo 完成,(c) 1987-2022。
- openprocessing:由 Naoki Tsutae 完成的四叉樹
-
曼德布羅多執行緒
-
迭代視覺化
// Quad-tree by Naoki Tsutae in Processing // https://openprocessing.org/sketch/1769288 quadTree = (x, y, size) => { if (size < minRectSize) return; const n = noise((x + posx) * 0.001, (y + posy) * 0.001, variation); if (abs(n - 0.45) > size / maxRectSize) { rect(x, y, size); } else { size /= 2; const d = size / 2; quadTree(x + d, y + d, size); quadTree(x + d, y - d, size); quadTree(x - d, y + d, size); quadTree(x - d, y - d, size); } };
區域四叉樹表示空間劃分,透過將區域分解為四個相等的象限、子象限等等,每個葉節點包含與特定子區域相對應的資料。樹中的每個節點要麼具有
- 正好四個子節點
- 或者沒有子節點(葉節點)。
遵循這種分解策略的四叉樹的高度(即,只要在子象限中有感興趣的資料,就細分子象限)對正在分解的空間中感興趣區域的空間分佈敏感且依賴於此。區域四叉樹是一種trie。
深度為 n 的區域四叉樹可用於表示包含 2n × 2n 個畫素的影像,其中每個畫素值均為 0 或 1。根節點表示整個影像區域。如果任何區域中的畫素並非完全為 0 或 1,則將其細分。在此應用中,每個葉節點表示一個畫素塊,這些畫素塊均為 0 或 1。請注意,當這些樹用於儲存影像時,在空間方面可能會有潛在的節省;影像通常有許多大小可觀的區域,在整個區域中具有相同的顏色值。與其儲存影像中每個畫素的二維陣列,不如使用四叉樹來捕獲可能比我們否則需要畫素解析度大小的單元高出許多劃分級別的相同資訊。樹解析度和整體大小受畫素大小和影像大小的限制。
區域四叉樹還可以用作資料場的可變解析度表示。例如,區域中的溫度可以儲存為四叉樹,每個葉節點儲存其表示的子區域的平均溫度。
Once b [the exterior distance estimate for c] is found, by the Koebe 1/4-theorem, we know there's no point of the Mandelbrot set with distance from c smaller than b/4.
// code in Haskell by Claude Heiland-Allen https://mathr.co.uk/blog/2010-10-30_distance_estimation.html
exterior :: Square -> Bool
exterior s@(Square a b c d) = fromMaybe False $ do
lb <- distance a
lt <- distance b
rb <- distance c
rt <- distance d
let k = 4 * sqrt 2 * size s
return $ and
[ lb + rb > k
, lt + rt > k
, lb + lt > k
, rb + rt > k
]

超取樣或超取樣抗鋸齒 (SSAA) 是一種空間抗鋸齒方法,即用於從計算機遊戲中渲染的影像或生成影像的其他計算機程式中消除鋸齒(鋸齒狀和畫素化邊緣,俗稱“鋸齒”)的方法。鋸齒的出現是因為與具有連續平滑曲線和線條的現實世界物體不同,計算機螢幕向觀看者顯示大量的小方塊。這些畫素大小相同,每個畫素都有單一顏色。線條只能顯示為畫素集合,因此除非它是完全水平或垂直的,否則看起來會很鋸齒。超取樣的目的是減少這種效果。在畫素內部的多個例項(而不僅僅是在中心,像正常情況一樣)進行顏色取樣,然後計算平均顏色值。這是透過以比要顯示的解析度高得多的解析度渲染影像,然後將其縮小到所需大小,並使用額外的畫素進行計算來實現的。結果是降取樣的影像,在物體邊緣的畫素行之間具有更平滑的過渡。
樣本數量決定了輸出質量。
- TechInfo - 由 Michael Condron 提供的抗鋸齒
- Fract (Lisp 程式碼) 由 Yannick Gingras 提供
- 維基百科上的空間抗鋸齒[11]
- 分形論壇討論:分形的抗鋸齒 - 最佳方法?[12]
- 超級取樣
-
超級取樣影像示例
-
超級取樣的 Cpp 程式碼
-
帶鋸齒的棋盤 - 影像和 C 原始碼
超級取樣,其他名稱
計算成本和自適應超級取樣
[edit | edit source]超級取樣在計算上很昂貴,因為它需要更大的顯示卡記憶體和記憶體頻寬,因為使用的緩衝區大小要大得多。[16] 解決這個問題的一種方法是使用稱為自適應超級取樣的技術,它只對物體邊緣的畫素進行超級取樣。
最初,每個畫素內只取幾個樣本。如果這些值非常相似,則只使用這些樣本確定顏色。如果不是,則使用更多樣本。這種方法的結果是,只有在必要的地方才會計算更多樣本,從而提高效能。
型別
[edit | edit source]在畫素內取樣時,必須以某種方式確定樣本位置。雖然這樣做的方法數量是無限的,但有一些方法是常用的。[16][17]
-
均勻分佈的網格演算法
-
旋轉網格演算法(樣本密度為 2 倍)
-
隨機演算法
-
抖動演算法
-
泊松圓盤演算法
-
準蒙特卡羅方法演算法
-
N 皇后
-
RGSS
-
高解析度抗鋸齒 (HRAA),五邊形
-
翻轉四邊形
-
翻轉三角形
網格
[edit | edit source]最簡單的演算法。畫素被分成幾個子畫素,每個子畫素的中心都會取一個樣本。它快速且易於實現。但是,由於取樣的規律性,如果使用的子畫素數量較少,仍然會發生鋸齒。
隨機
[edit | edit source]也稱為隨機取樣,它避免了網格超級取樣的規律性。但是,由於模式的不規則性,樣本在畫素的某些區域會變得不必要,而在其他區域則會缺失。[18]
泊松圓盤
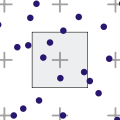
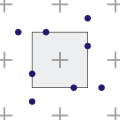
[edit | edit source]-
使用泊松圓盤取樣生成的點樣本,以及最小點間距離的圖形表示
泊松圓盤取樣演算法[19] 將樣本隨機放置,然後檢查任何兩個樣本是否過於接近。最終結果是均勻但隨機的樣本分佈。但是,該演算法所需的計算時間過長,不適合用於即時渲染,除非取樣本身在計算上比樣本點的定位更昂貴,或者樣本點不會為每個畫素重新定位。[18]
Poisson-disk sampling (blue noise) is the best sampling pattern. It maximizes the uniformity of the samples in addition to the randomness of their placement, which gets you the most bang for your buck with respect to the contribution of each sample. quaz0r on FF
連結
抖動
[edit | edit source]對網格演算法的修改,以近似泊松圓盤。畫素被分成幾個子畫素,但樣本不是從每個子畫素的中心取的,而是從子畫素內的隨機點取的。聚集仍然可能發生,但程度較小。[18] 抖動也被推薦用於避免莫爾紋。
旋轉網格
[edit | edit source]使用 2×2 網格佈局,但樣本模式被旋轉,以避免樣本與水平或垂直軸對齊,這極大地提高了最常見情況下的抗鋸齒質量。為了獲得最佳模式,旋轉角度為 arctan (12)(約 26.6 度),正方形被拉伸了倍。[20] [citation needed]
具有極端偽隨機鋸齒的影像示例
[edit | edit source]因為分形具有無限的細節,並且除了算術舍入誤差之外沒有噪聲,所以它們比照片或其他測量資料更清晰地說明了鋸齒。逃逸時間(它們在畫素的精確中心轉換為顏色)在集合的邊界處趨於無窮大,因此,由於鋸齒,靠近邊界的中心的顏色是不可預測的。此示例在其大約一半的畫素中都有邊緣,因此它顯示出許多鋸齒。第一張影像以其原始取樣率上傳。(由於大多數現代軟體都會進行抗鋸齒處理,因此可能需要下載完整尺寸的版本才能看到所有鋸齒。)第二張影像以五倍的取樣率進行計算,然後使用抗鋸齒進行下采樣。假設人們真的想要每個畫素的平均顏色,那麼這張影像就更接近了。它明顯比第一張影像更有序。
為了正確比較這些影像,有必要以全尺寸檢視它們。
-
1. 使用程式“MandelZot”計算
-
2. 透過模糊和下采樣五倍進行抗鋸齒處理
-
3. 對邊緣點進行插值,然後進行抗鋸齒處理並進行下采樣
-
4. 對從上一張影像中刪除的點進行增強
-
5. 再次下采樣,不進行抗鋸齒處理
在這種情況下,碰巧有額外的資訊可用。透過使用“距離估計器”演算法重新計算,識別出了非常靠近集合邊緣的點,因此,集合邊緣附近快速變化的逃逸時間會將異常精細的細節混疊進來。從這些計算出的點得出的顏色已被識別為其畫素的異常不具有代表性。集合在那裡變化得更快,因此單個點樣本不能代表整個畫素。在第三張影像中,這些點被替換為周圍點的插值。這減少了影像的噪點,但也有使顏色變亮的副作用。因此,此影像與透過更大的計算點集獲得的影像不完全相同。為了顯示被丟棄了什麼,第四張影像顯示了被拒絕的點,這些點被混合到灰色背景中。
最後,“發芽渦輪機”非常規則,因此在向下取樣以獲取最近的畫素時,在主“渦輪軸”附近可以清楚地看到系統性的(莫爾)混疊。第一張影像中的混疊看起來是隨機的,因為它來自畫素大小以下的所有細節級別。當抑制較低級別的混疊以製作第三張影像,然後再次對第三張影像進行降取樣(無抗鋸齒)以製作第五張影像時,第三張影像尺度上的順序在第五張影像中表現為系統性的混疊。
影像的純降取樣具有以下效果(建議全尺寸檢視)
-
1) Mandelbrot 集合 的特定螺旋特徵的圖片
-
2) 每個畫素 4 個樣本
-
3) 每個畫素 25 個樣本
-
4) 每個畫素 400 個樣本
程式碼
[edit | edit source]- 由 使用者 Geek3 編寫的 Cpp 程式碼
// subpixels finished -> make arithmetic mean
char pixel[3];
for (int c = 0; c < 3; c++)
pixel[c] = (int)(255.0 * sum[c] / (subpix * subpix) + 0.5);
fwrite(pixel, 1, 3, image_file);
//pixel finished
- Ned Batchelder[21] 的 Aptus 命令列版本(python 和 c 程式碼)(參見 aptuscmd.py)使用透過 PIL 函式 resize[22] 的高質量降取樣濾波器
- Josef Jelinek 編寫的 Java 程式碼:[23] 使用網格演算法進行超取樣,計算 4 個新點(角點),產生的顏色是每個顏色分量的平均值
//Created by Josef Jelinek
// http://java.rubikscube.info/
Color c0 = color(dx, dy); // color of central point
// computation of 4 new points for antialiasing
if (antialias) { // computes 4 new points (corners)
Color c1 = color(dx - 0.25 * r, dy - 0.25 * r);
Color c2 = color(dx + 0.25 * r, dy - 0.25 * r);
Color c3 = color(dx + 0.25 * r, dy + 0.25 * r);
Color c4 = color(dx - 0.25 * r, dy + 0.25 * r);
// resulting color; each component of color is an avarage of 5 values (central point and 4 corners)
int red = (c0.getRed() + c1.getRed() + c2.getRed() + c3.getRed() + c4.getRed()) / 5;
int green = (c0.getGreen() + c1.getGreen() + c2.getGreen() + c3.getGreen() + c4.getGreen()) / 5;
int blue = (c0.getBlue() + c1.getBlue() + c2.getBlue() + c3.getBlue() + c4.getBlue()) / 5;
color = new Color(red, green, blue);
}
- 可以建立大影像(例如 10 000 x 10 000),並將其轉換/調整大小(縮小)。例如使用 ImageMagick
convert big.ppm -resize 2000x2000 m.png
降取樣和插值本質上是壓縮,低頻分量,即
- 變化速度低於取樣頻率一半的緩慢變化顏色將被保留
- 高頻細節將丟失
區間算術
[edit | edit source]如何最佳化搜尋最近的點?
[edit | edit source]另請參閱
[edit | edit source]- Tessellation 是將空間劃分為一組較小多邊形的過程
- 2D 網格型別
- commons:Category:Mesh in computer graphics
- 取樣和影像噪聲 - dither 用於更準確地顯示包含比顯示硬體能夠顯示的更大範圍顏色的圖形
- Fractint 繪製方法[30]
- Steven Stoft 編寫的 Fratal Witchcraft 繪製方法[31]
- AlmondBread 演算法 [32]
- rugh 集方法 [33]
- 細胞對映 基於區間算術,在圖中使用標籤傳播以避免函式迭代和舍入誤差 [34]
- “我們將基於區間算術的細胞對映與圖中的標籤傳播相結合,以避免函式迭代和舍入誤差。” - Luiz Henrique de Figueiredo 等人[35][36]
- 使用外部距離估計[37] 和 Koebe 四分之一定理
- 使用 對稱
參考資料
[edit | edit source]- ↑ 來自塔爾圖大學的紋理和取樣:
- ↑ fractalforums.org : 取樣
- ↑ “您可以信賴的 Julia 集影像” - Luiz-Henrique de Figueiredo、Diego Nehab、Jofge Stolfi、Joao Batista Oliveira - IEE 2015
- ↑ 維基百科中的超取樣
- ↑ 維基百科中的亞畫素解析度
- ↑ researchgate : 基於梯度的區域性分形分析的單影像超解析度和細節增強 - HONGTENG Xu、Xiaokang Yang、Guangtao Zhai
- ↑ Hongteng Xu: 基於分形的影像處理
- ↑ wolfram mathematica: AdaptiveSamplingOfSurfaces
- ↑ 自適應取樣,繪製數學曲線 By Xah Lee. Date: 2016-05-01. Last updated: 2016-05-07.
- ↑ 來自 Mandelbrot 集合詞彙表和百科全書,作者:Robert Munafo,(c) 1987-2020. 由 Robert P. Munafo 於 2010 年 12 月 5 日編寫的指數對映。
- ↑ 維基百科中的空間抗鋸齒
- ↑ fractalforums 討論:抗鋸齒分形 - 最佳方法?
- ↑ 維基百科中的超取樣
- ↑ ImageMagick v6 示例 - 重取樣濾波器
- ↑ 哪個影像降取樣演算法的質量最好?
- ↑ a b "抗鋸齒技術比較". sapphirenation.net. 2016-11-29. 檢索於 2020-04-19.
一般來說,SSAA 提供卓越的影像質量,但效能損失很大,因為場景是在非常高的解析度下渲染的。
- ↑ "什麼是超取樣?". everything2.com. 2004-05-20. 檢索於 2020-04-19.
- ↑ a b c Allen Sherrod (2008). 遊戲圖形程式設計. Charles River Media. p. 336. ISBN 978-1584505167.
- ↑ Cook, R. L. (1986). "計算機圖形中的隨機取樣". ACM 圖形學報. 5 (1): 51–72. doi:10.1145/7529.8927. S2CID 8551941.
- ↑ "超取樣抗鋸齒分析" (PDF). Beyond3D.com. 檢索於 2020-04-19.
- ↑ Aptus (python 和 c 程式碼) by Ned Batchelder
- ↑ Pil 函式 resize
- ↑ Java 程式碼 by Josef Jelinek
- ↑ 你可以信任的 Julia 集影像 Luiz Henrique de Figueiredo
- ↑ 關於複雜動力系統雙曲結構的數值構建 by Jennifer Suzanne Lynch Hruska
- ↑ "你可以信任的 Julia 集影像" by Luiz Henrique de Figueiredo 和 Joao Batista Oliveira
- ↑ 生成 Julia 集保證影像的自適應演算法 by Luiz Henrique de Figueiredo
- ↑ 用區間算術繪製分形 - 第 1 部分 by Dr Rupert Rawnsley
- ↑ 用區間算術繪製分形 - 第 2 部分 by Dr Rupert Rawnsley
- ↑ Fractint 繪製方法
- ↑ 同步軌道演算法 by R Munafo
- ↑ 杏仁麵包主頁 by Michael R. Ganss
- ↑ 粗略的 Mandelbrot 集 by Neural Outlet.. 發表於 2014 年 11 月 23 日
- ↑ 你可以信任的 Julia 集影像 by Luiz Henrique de Figueiredo, Diego Nehab, Jorge Stolfi 和 Joao Batista Oliveira
- ↑ 多項式 Julia 集的嚴格邊界 by Luiz Henrique de Figueiredo
- ↑ 你可以信任的 Julia 集影像 by LUIZ HENRIQUE DE FIGUEIREDO 和 DIEGO NEHAB
- ↑ 距離估計 by Claude Heiland-Allen