此頁面介紹：扭曲的微型曼德勃羅集，島嶼的扭曲（曼德勃羅集和引數平面的一部分）。

名稱

曼德勃羅集在其自身內部的微型副本有很多名稱

小型曼德勃羅集
迷你曼德勃羅集
嬰兒曼德勃羅集
嬰兒勃羅
蟲
島嶼：“島嶼”一詞由貝努瓦·曼德勃羅在其關於《自然的分形幾何》中對曼德勃羅集的描述中引入” 羅伯特·穆納福
島嶼 μ-分子
嵌入的曼德勃羅集副本
曼德勃羅蒂
侏儒
迷你勃羅
原始 M 副本
原始形狀略微變形後的副本
曼德勃羅集在其自身內部的近似副本

扭曲的不同名稱^[1]

扭曲的微型曼德勃羅集的名稱

扭曲的微型曼德勃羅集

示例

中心為 c = 0.359259224758007 +0.642513737138542 i，週期為 5 的迷你曼德勃羅集，位於 1/4 尾跡中
c = -0.77028065155993652446 by -0.11144667326007166574 放大倍數：281748
mag =2369369 中心座標 (-0.175875248 , 1.075392007 )
中心：-0.164,1.032；寬度/高度：0.04
週期為 36 的島嶼，中心為 c = -0.763926983955582 +0.092287538419582 i，來自週期為 2 的分量的 1/34 子尾跡

參見

commons:Category:Near-copies_of_the_Mandelbrot_set_within_itself

來自象谷的一系列位置，週期倍增（由克勞德·海蘭德-艾倫提供）^[4]

# period	 center 			                radius
     4 	-1.565201668337550811e-01+ 1.032247108922831780e+00 i 	1.697e-02
     8 	4.048996651751222142e-01 + 1.458203637665893004e-01 i 	2.743e-03
    16 	2.925037532341934199e-01 + 1.492506899834379792e-02 i 	3.484e-04
    32 	2.602618199285006706e-01 + 1.667791320926506355e-03 i 	4.113e-05
    64 	2.524934589775105209e-01 + 1.971526796077277316e-04 i 	4.920e-06
   128 	2.506132008410751344e-01 + 2.396932642510365971e-05 i 	5.997e-07
   256 	2.501519680089798192e-01 + 2.954962325906881015e-06 i 	7.398e-08
   512 	2.500378219137852631e-01 + 3.668242052764790239e-07 i 	9.185e-09
  1024 	2.500094340031833728e-01 + 4.569478652064613658e-08 i 	1.144e-09
  2048 	2.500023558032561377e-01 + 5.701985912706845832e-09 i 	1.428e-10
  4096 	2.500005886128087162e-01 + 7.121326948562731412e-10 i 	1.783e-11
  8192 	2.500001471109009610e-01 + 8.897814201389539302e-11 i 	2.228e-12

marcm200 編制的列表

cardioid       angle             
period p       p<-2p->4p         eccentricity   cardioid center
------------------------------------------------------------------------------------------------------
5              177.1             1.35           0.35925922475800742273-0.64251373713854231795*i
6              176.5             1.47           0.4433256333996235532-0.37296241666284651872*i
7              176.1             1.55           0.43237619264199450564-0.22675990443534863039*i
8              175.8             1.52           0.40489966517512215871-0.14582036376658927268*i
10             175.4             1.65           0.35681724849231194474-0.069452865466830299157*i
12             175.1             1.72           0.32558950955066034982-0.038047880934755723414*i
15             174.8             1.79           0.29844800890399547644-0.018383367322073254635*i
17             174.7             1.80           0.28756611704687790043-0.012281055409848253349*i
21             174.6             1.84           0.27436979919551240936-0.0062585874913430950342*i
25             174.5             1.87           0.2652783219046058732 -0.0037120599898783183101*i
31             174.4             1.90           0.26095224231422198269-0.0018410978175303128503*i
43             174.34            1.91           0.2556052938434967281 -0.00066797029763820438275*i

位置

0,25000102515011806826817597033225524583655 + 0,0000000016387052819136931666219461i 放大倍數 = 6,871947673*(10^10) 所以半徑 = 0.14556040756914119* 10^{-10}
0.2925294 + 0.0149698 i @ 0.0006675
c = 0.292503753234193 -0.014925068998344i 週期 = 16，影像大小 +0.0005 ^[5]
by marcm200
- 週期 7 c =0.43237619264199450564-0.22675990443534863039i
- 週期 14 c=0.4325688150887696537-0.22873440581356344059i
- 週期 28 c=0.43266973566541755414-0.22933968667591089763i

自相似性

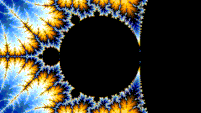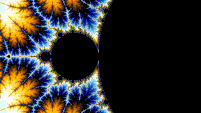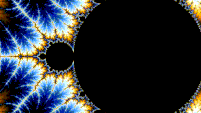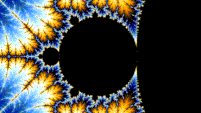
曼德勃羅集在 Misiurewicz 點的鄰域中放大時是自相似的。據推測，它在廣義費根鮑姆點（例如，−1.401155 或 −0.1528 + 1.0397i）周圍也是自相似的，從收斂到極限集的意義上講。^[6]^[7] 總體而言，曼德勃羅集不是嚴格自相似的，但它是準自相似的，因為可以在任意小的尺度上找到其自身略微不同的較小版本。這些曼德勃羅集的小副本都略有不同，主要是因為連線它們與集合主體之間的細線。

"this combination of familiarity (small copies of the Mandelbrot set) and novelty (subtly distorted, differently decorated) that make the Mandelbrot set much more interesting than the fractals generated by IFS."^[8]

問答

它們是完全相同的副本嗎？

它們是

不是完全相同的副本
略微變形後的副本
近似自相似的副本
與整個曼德勃羅集擬共形等價
準自相似
嬰兒曼德勃羅集不是完全自相似的。嬰兒曼德勃羅集與原始曼德勃羅集同胚

為什麼曼德勃羅集包含自身的副本？

為什麼曼德勃羅集包含（略微變形後的）自身的副本？^[9]

“重整化解釋了為什麼會出現嬰兒曼德勃羅集：嬰兒曼德勃羅集中的所有二次多項式都進行重整化，並且所有都以本質上相同的方式進行重整化。”
“分形是反射的反射的反射……”
“迭代創造複雜性。曼德勃羅集基於對無限序列行為的檢查。該序列的行為非常複雜。事實上，它可能是混沌的。我們正處於對初始條件的敏感依賴（也稱為蝴蝶效應）之中。” ^[10]
“雖然過程非常簡單，但由於過程的迭代性質，根據您開始時複平面上點的不同，會導致截然不同的結果。”

為什麼其他分形中存在曼德勃羅集的副本？

曼德勃羅集是通用的^[11]，因此可以在以下位置找到

迭代復對映^[12]
引數化全純函式族的分岔軌跡：有理函式族，超越函式族 ^[13]
任何全純有理對映族的分岔軌跡^[14]
Douady 和 Hubbard 的類二次對映 ^[15]

如何描述迷你勃羅？

測量指標

主偽心形線的週期
主偽心形線的中心
引數平面的視窗（半徑和中心）
落在偽心形線尖點上的外部射線的角度
主偽心形線的大小
方向
變形

如何計算大小和方向？

大小和方向

混沌動力系統的週期n視窗的縮放

葉夫根尼·德米多夫的週期性縮放視窗
J.A.Yorke、C.Grebogi、E.Ott和L.Tedeschini-Lalli，“耗散動力系統中視窗的縮放行為”，物理評論快報54，1095（1985）
B.R.Hunt、E.Ott，“二次對映的有序和混沌引數依賴性中的結構”，J.Phys.A 30（1997），7067。
克勞德·海蘭德-艾倫推導尺寸估計
克勞德·海蘭德-艾倫的近似自相似性
- 克勞德·海蘭德-艾倫的mandelbrot-graphics庫中的m-island-zoom.c

大小和方向的公式

 $r={\frac {1}{\beta \Lambda _{p}^{2}}}$

輸入和相關值

迷你布羅特主偽心形線的核 $c$
迷你布羅特主偽心形線的週期 $p$
$\beta$
$\Lambda _{n}$
$\lambda _{n}$

輸出

複數大小和方向估計r（複數）。要計算它，只需對結果使用arg和abs

其中

 $z_{1}=0;z_{n+1}=z_{n}^{2}+c$

 $\lambda _{n}=2z_{n}$

 $\Lambda _{n}=\lambda _{2}\lambda _{3}\cdots \lambda _{n}$ 

 $\beta =1+\Lambda _{2}^{-1}+\Lambda _{3}^{-1}+\dots +\Lambda _{p}^{-1}$

如何使用？

"if the nucleus of the baby is c and the complex size is r , there is another miniature copy near the baby around  $c+rc$  with size approximately  $r^{2}$ " 	Claude Heiland-Allen

迷你布羅特示例

週期3，靠近-2
週期4，靠近i
週期5，靠近-1.5+0.5i

另請參見克勞德·海蘭德-艾倫的mandelbrot-numerics庫中的c函式m_size

// mandelbrot-numerics -- numerical algorithms related to the Mandelbrot set
// Copyright (C) 2015-2018 Claude Heiland-Allen
// License GPL3+ http://www.gnu.org/licenses/gpl.html

#include <mandelbrot-numerics.h>

extern double _Complex m_d_size(double _Complex nucleus, int period) {
  double _Complex l = 1;
  double _Complex b = 1;
  double _Complex z = 0;
  for (int i = 1; i < period; ++i) {
    z = z * z + nucleus;
    l = 2 * z * l;
    b = b + 1 / l;
  }
  return 1 / (b * l * l);
}

面積

週期p+1的島嶼的面積 $A$ 由羅伯特·穆納福給出的公式近似表示：^[16]

$A_{p+1}\approx 0.05{\frac {sin^{2}({\frac {\pi }{p}})}{p^{4}}}$

如何測量變形？

測量

用0的原像處迭代的導數來表示這些^[17]
衛星半徑與主心形線半徑之比
次級（子）分量的角位置
以度數（或弧度）表示，因為迷你布羅特的各個部分只是旋轉（保角變換）
到尖點的兩個距離之比^[18]
“使用一種演算法測量了曼德勃羅集中的扭曲侏儒，該演算法允許在找到任何侏儒的頭部和心形原子（北和南）的位置，一旦將游標放在計算機終端上的任何侏儒內部。我們描述了侏儒的兩種變形：線性變形和角度變形。當在南北角平面中繪製南北角時，會形成點族。來自曼德勃羅集的海馬谷和其他侏儒海馬谷（無論是在尖刺上還是在原子上的卷鬚上）的扭曲侏儒的角度和距離測量值在南北平面的一個部分緊密地聚集在一起。來自心形表面主要原子上方卷鬚的扭曲侏儒的測量值在南北平面的另一部分緊密地聚集在一起。這種看待曼德勃羅集的不同方式提供了一種研究侏儒變形的有意思的方法。” A. G. 戴維斯·菲利普、邁克爾·弗雷姆、亞當·羅布奇：曼德勃羅集中的扭曲侏儒。計算機與圖形18(2)：239-248 (1994)

偽心形線的偏心率

偽心形線的偏心率以幾何方式計算，並定義為從尖點到（待補充）的兩個距離之比。

$ecc={\frac {cusp_{B}}{cusp_{A}}}$

子分量的位置

2個分量
- 父分量（週期=p的偽心形線）=p-分量
- 子分量（週期=2*p的偽圓）=2p-分量
父分量（偽心形線）內部的兩條線
- 父分量（偽心形線）下半部分的軸線=穿過兩點的直線：偽心形線的核和尖點=下軸線
- 父分量上半部分的軸線=穿過兩點的直線：核和根點（子分量和父分量之間）=上軸線
以圈數為單位測量的兩條線之間的角度
- 無變形時為0=所有3個點都在同一條線上（例如，整個M集以主心形線作為父分量，週期2分量作為子分量的情況）
- 變形時>0

用數學語言來說，透過兩點

$z_{1}=x_{1}+y_{1}*i$
$z_{2}=x_{2}+y_{2}*i$

的直線的斜率 m 為

m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.

斜率為 $m_{1}$ 和 $m_{2}$ 的兩條直線之間的夾角是^[19]

 $\tan ^{-1}{\dfrac {m_{1}-m_{2}}{1+m_{1}m_{2}}}$

這裡有一個 C 函式^[20]

 
// Function to find the angle between two lines. Each line is defined by 2 points
double findAngleBetweenLines(const complex double z1a, const complex double z1b, const complex double z2a, const complex double z2b)
{
	// slope of line 1 and 2 
	double m1 = (cimag(z1a) - cimag(z1b))/(creal(z1a) - creal(z1b));
	double m2 = (cimag(z2a) - cimag(z2b))/(creal(z2a) - creal(z2b));
	
	double angle = abs((m2 - m1)/ (1 + m1 * m2));

	// Calculate tan inverse of the angle
	double ret = atan(angle);

	// Convert the angle from radian to degree
	double val = (ret * 180) / PI;

	// return the result
	return val;
}

迷你分形集可以有多扭曲？

迷你分形集的最大扭曲度是多少？^[21]

如何找到迷你分形集？

定位 = 查詢^[22]

如何找到扭曲的迷你分形集？

使用曼德勃羅集圖形庫和程式：m-warped-midgets

扭曲與島嶼的其他度量之間有什麼關係？

偏心率隨著週期的增加而增加，但不是線性增加，甚至不是單調增加。^[23]
尾跡中最大的島嶼是最扭曲的。m/n 尾跡中最大的迷你分形集的週期是 n+1

參見

如何找到落在任何曼德勃羅集分量的根點上的外部射線的角度，而該分量無法透過有限次數的邊界穿越從主心形（M0）訪問？

參考文獻

[1] 維基百科中的畸變（光學）

[2] 維基百科中的影像扭曲

[3] 孫雨榮的二維網格扭曲

[4] ractalforums.com：迷你分形集可以有多扭曲？

[5] 羅伯特·P·穆納福的扭曲，2010 年 10 月 20 日。來自曼德勃羅集詞彙表和百科全書

[6] Lei (1990). "曼德勃羅集和朱利亞集之間的相似性". 數學物理通訊. 134 (3): 587–617. Bibcode:1990CMaPh.134..587L. doi:10.1007/bf02098448. S2CID 122439436.

[7] J. Milnor (1989). "曼德勃羅集中的自相似性和毛髮性". 在 M. C. Tangora（編輯）中。 幾何與拓撲中的計算機. 紐約：泰勒和弗朗西斯。第 211-257 頁。 ISBN 9780824780319.)

[8] 曼德勃羅集和朱利亞集。曼德勃羅集 - 耶魯大學分形幾何邁克爾·弗雷姆、貝努瓦·曼德勃羅（1924-2010）和尼爾·內格爾 2022 年 11 月 24 日的小副本

[9] th.stackexchange 問題：為什麼曼德勃羅集包含其自身的略微變形副本？

[10] th.stackexchange 問題：曼德勃羅集分形 - 如何可能？

[11] 曼德勃羅集是普適的，作者：柯蒂斯·T·麥克米倫

[12] Quora：為什麼曼德勃羅集很重要？

[13] th.stackexchange問題：當我使用牛頓法求逆時，為什麼會出現曼德勃羅集？

[14] th.stackexchange問題：除了曼德勃羅集之外，其他分形中是否已知存在迷你曼德勃羅集？

[15] 曼德勃羅集的普適性，來自耶魯大學分形幾何，作者：邁克爾·弗雷姆，貝努瓦·曼德勃羅（1924-2010）和尼爾·內格

[16] 主序列，作者：羅伯特·P·穆納福，2009年11月5日，來自曼德勃羅集詞彙表和百科全書

[17] th.stackexchange問題：迷你曼德勃羅集是精確複製嗎？

[18] ractalforums.org：迷你曼德勃羅集中的倍週期現象

[19] th.stackexchange問題：如何找到兩條直線之間的夾角？

[20] 兩條直線之間的夾角，來自geeksforgeeks

[21] ractalforums.com：迷你曼德勃羅集可以有多扭曲？

[22] th.stackexchange問題：“如何找到迷你曼德勃羅集？”

[23] ractalforums.org：迷你曼德勃羅集中的倍週期現象

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]