分形/複平面中的迭代/cremer


The problem is that we are exploring environments based upon irrational numbers through computer machinery which works with finite rationals ! ( Alessandro Rosa )
- 存在二次多項式的 Cremer Julia集,
- 沒有此類 Julia集的影像
- Cremer Julia集沒有內部,並且永遠不會斷開平面 [1]
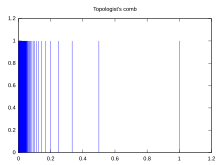
- 它包含單個或雙 梳。 [2] "人們期望在 刺蝟 中找到諸如梳子(康託集和區間乘積的同胚)之類的物體。"(Kingshook Biswas [3]
- Cremer Julia集不是區域性連通的 [4][5]
- "與無差異非線性化不動點相關的刺蝟是完全非平凡的緊緻連通集,完全由動力學不變。" R. PEREZ-MARCO [6]
- Cremer 不動點屬於 Julia 集 [7]
對於 Cremer Julia 集,內部角應該是非布里尤諾數(無理數,非丟番圖)。
"Cremer 引數位於雙曲分量的邊界,在特定的內部角(乘數的幅角)處。如果您知道角度,則可以顯式地計算出週期為 1、2、3 的引數,並且對於所有周期,可以數值計算。如果我沒記錯的話,一個簡單的角度是 0.01001000100001000001 ... 乘以 2PI。但是,當然有 西格爾角 和 拋物角,它們在前 100 位數字上是相同的。從數值上講,Cremer、區域性連通的西格爾、非區域性連通的西格爾以及具有高旋轉數的拋物線之間沒有區別。... 也許這就是為什麼你無法繪製它們的原因之一..." Wolf Jung
"Cremer 內部角獲得為 0.10001000000000000010000...,具有快速增長的 0 間隙,但任何有限近似都是拋物線的。"(Wolf Jung)
可以將 Cremer Julia 集視為具有 西格爾圓盤 的 Julia 集,具有無限多個 數字。
(具有無限週期的拋物線 Julia 集 = 具有非常高週期的拋物線填充 Julia 集可能看起來類似於西格爾 Julia 集)
模型
- Rempe 的直刷模型
- Cheritat 的偽刺蝟 [8]
描述 [9]
"“小週期性質”:原點的每個鄰域都包含無限多個週期軌道"(LIA PETRACOVICI 的 CREMER 不動點和小週期)[12]
"對於 Cremer 引數,存在唯一的引數射線著陸,但動力學更加複雜。"(Wolf Jung)
著陸在 Cremer 和西格爾引數點 c 上的外部射線的角度是什麼?
那些不屬於任何封閉尾跡的。它們是無理的,我想沒有更多已知的資訊。您可以使用合適的尾跡的角度來近似它們......
這類似於透過依次移除開區間來構造中間 1/3 標準康託集。
- 從 [0,1] 開始。
- 刪除 (1/3, 2/3)。
- 刪除 (1/7, 2/7) 和 (5/7, 6/7)
- ...
剩下的角度是一個康託集,它們是所有著陸在主心形上的射線的角度。有理角屬於根,無理角屬於西格爾和克萊默引數。此外,每個有理角都是有限步之後移除的區間的邊界點。因此,在以下移除閉區間的構造中,您不會得到康託集,只有無理角會保留
- 從 [0,1] 開始。
- 刪除 [1/3, 2/3]。
- 刪除 [1/7, 2/7] 和 [5/7, 6/7]
- 構造 [13]
- ↑ mathoverflow.net 問題:連通全純動力學的收縮性/149170#149170
- ↑ DAN ERIK KRARUP SØRENSEN 透過拋物線擾動描述二次克萊默點多項式。遍歷理論與動力系統 (1998), 18 : pp 739-758. 1998 年劍橋大學
- ↑ Kingshook Biswas 的豪斯多夫維數為 1 的刺蝟
- ↑ 維基百科:區域性連通空間
- ↑ Kingshook Biswas 的刺蝟內部的平滑梳子
- ↑ Ricardo Pérez-Marco 的關於擬不變曲線的
- ↑ LIA PETRACOVICI 的某些具有克萊默點的有理函式的不可接近臨界點
- ↑ Cheritat 影像庫
- ↑ Mitsuhiro Shishikura 的全純函式非理性無差異不動點的動力學圖
- ↑ Alessandro Rosa 的使用康託集、豪斯多夫和劉維爾捕獵刺蝟
- ↑ 維基百科:刺蝟空間
- ↑ LIA PETRACOVICI 的 CREMER 不動點和小週期
- ↑ M. BRAVERMAN 和 M. YAMPOLSKY 的構造不可計算的 JULIA 集
- Pérez-Marco, R. (1994)。Julia 集和刺蝟的拓撲。法國奧賽:巴黎-南大學,數學系。版本/格式:印刷書籍:英語,系列名稱:預出版物(巴黎-南大學。數學系),第 94-48 號。
- 二次克雷莫多項式的Julia集。作者:Alexander Blokh, Lex Oversteegen。doi:10.1016/j.topol.2006.02.001拓撲及其應用。第153卷,第15期,2006年9月1日,第3038-3050頁
- 維基百科:劉維爾數
- 為什麼黃金分割是最優的:一個關於丟番圖數、布里尤諾數和劉維爾數的介紹 - 鄭和
- 學者百科詞條由Xavier Buff撰寫:Siegel圓盤
- 關於刺蝟動力學的未解問題
- 某些具有克雷莫點的有理函式的不可達臨界點,作者:Lia Petracovici
- 克雷莫多項式的不可達臨界點,作者:Jan Kiwi
- 任意次數的基本單克雷莫多項式的Julia集,作者:Alexander Blokh
- 基本二次克雷莫多項式的太陽Julia集,作者:A. Blokh, X. Buff, A. Chéritat, L. Oversteege([提交於2008年12月5日]
- 刺蝟資源
