交通基礎/水平曲線

水平曲線 是公路幾何設計中兩個重要的過渡元素之一（另一個是豎曲線）。水平曲線提供兩段直線型路段之間的過渡，允許車輛以逐漸的速率而不是急轉彎的方式完成轉彎。曲線的設計依賴於道路的預期設計速度，以及其他因素，包括排水和摩擦力。這些曲線是半圓形，以提供駕駛員恆定的轉彎速率，其半徑由圍繞向心力的物理定律確定。

水平曲線的基本特性

物理特性

挪威奧斯陸的水平曲線

除了動量之外，當車輛轉彎時，還有兩種力作用於它。第一種是重力，它將車輛拉向地面。第二種是離心力，而它的反作用力，即向心加速度，則需要使車輛保持在彎曲的路徑上。對於任何給定的速度，對於更緊的轉彎（半徑較小）比更寬的轉彎（半徑較大），向心力需要更大。在水平表面上，側向摩擦力 $f_{s}$ 作為對抗離心力的力量，但它通常提供非常少的阻力/力量。因此，車輛必須在水平面上畫一個非常大的圓才能轉彎。

鑑於道路設計通常受限於非常狹窄的設計區域，因此通常不鼓勵進行寬轉彎。為了解決這個問題，水平曲線的設計師會將道路傾斜一定的角度。這種傾斜被稱為超高，或 $e$，即在給定一定行程的情況下，道路橫截面角度的上升量，也稱為坡度。超高在彎道上的存在使得一部分向心力可以由地面抵消，從而允許車輛以比平坦表面上允許的更快的速度完成轉彎。超高在降雨事件中也起到另一個重要作用，它有助於排水，因為水流過道路而不是積聚在道路上。通常，超高限制在 14% 以下，因為工程師需要考慮彎道上停放的車輛，因為那裡不存在向心力。

水平曲線的允許半徑 $R$ 可以透過知道預期的設計速度 $V$、摩擦係數和彎道上的允許超高來確定。

$R={\frac {v^{2}}{g\left({e+f_{s}}\right)}}\,\!$

有了這個半徑，從業人員就可以確定曲線的度數，以檢視它是否在可接受的標準範圍內。曲線的度數，$D_{a}$，可以透過以下公式計算，該公式以公制給出。

$\%R={\frac {1746}{D_{a}}}\%\,\!$

其中

• $D_{a}\,\!$= 曲線的度數 [30.5 米 (100 英尺) 弧線在水平曲線上的張角

超高應用

布里斯托爾賽車場

你會看到一個地方是汽車賽車場，那裡有陡峭的傾斜。這些賽道不在冬季運營，因此可以避免冬季天氣帶來的傾斜問題。司機也特別熟練，不過事故並不少見。對於 NASCAR 粉絲來說，以下表格可能會有所幫助。

表：美國賽道上的傾斜

賽道	長度（英里）	傾斜（度）
芝加哥汽車賽車場	1	0.00
英菲尼昂賽車場	1.949
沃特金斯格倫國際賽道	2.45
波科諾賽車場	2.5	6.00
邁阿密-霍姆斯特德賽車場	1.5	8.00
印第安納波利斯賽車場	2.5	9.00
孟菲斯賽車場	0.75	11.00
鳳凰國際賽車場	1	11.00
拉斯維加斯賽車場	1.5	12.00
馬丁斯維爾賽車場	0.526	12.00
新罕布什爾國際賽車場	1.058	12.00
加州賽車場	2	14.00
肯塔基賽車場	1.5	14.00
里士滿國際賽車場	0.75	14.00
堪薩斯賽車場	1.5	15.00
密歇根國際賽車場	2	18.00
納什維爾賽車場	0.596	18.00
北卡羅來納賽車場	1.017	22.00
達靈頓賽車場	1.366	23.00
亞特蘭大賽車場	1.54	24.00
多佛唐斯國際賽車場	1	24.00
Lowe's 汽車賽場	1.5	24.00
德克薩斯州汽車賽場	1.5	24.00
代託納國際賽車場	2.5	31.00
塔拉迪加超級賽車場	2.66	33.00
布里斯托爾賽車場	0.533	36.00

來源: FSN的夢幻賽車區

幾何屬性

典型的水平曲線（平面檢視）

水平曲線出現在兩條道路交叉的地方，為兩條道路之間提供平緩的過渡。兩條道路的交點定義為切點交點（PI）。曲線的起點位置定義為曲線起點（PC），而曲線的終點位置定義為切點（PT）。PC 距離 PI 為 $T$，其中 $T$ 被定義為切線長度。切線長度可以透過找到曲線的中心角（以度為單位）來計算。該角度等於兩條道路切線之間的內角的補角。

$T=R\tan \left({\frac {\Delta }{2}}\right)\,\!$

其中

• $T\,\!$= 切線長度（以長度單位為單位）
• $\Delta \,\!$= 曲線的中心角，以度為單位
• $R\,\!$= 曲線半徑（以長度單位為單位）

PT 距離 PC 為 $L$，其中 $L$ 被定義為曲線長度。曲線長度可以使用半圓長度公式確定

$L={\frac {R\Delta \pi }{180}}\,\!$

PI 和曲線頂點之間的距離可以很容易地使用 $T$ 和 $R$ 的直角三角形屬性來計算。取此距離並減去曲線半徑 $R$，可以找到外部距離 $E$，這是曲線和 PI 之間的最小距離。

$E=R\left({{\frac {1}{\cos \left({\frac {\Delta }{2}}\right)}}-1}\right)\,\!$

其中

• $E\,\!$= 外部距離（以長度單位為單位）

類似地，可以找到中垂線$M$。中垂線是連線 PC 和 PT 的直線與曲線的最大距離。它位於曲線頂點和 PI 之間的直線上。

$M=R\left({1-\cos \left({\frac {\Delta }{2}}\right)}\right)\,\!$

其中

• $M\,\!$= 中垂線（長度單位）

類似地，弦長的幾何公式可以找到$C$，它代表該曲線的弦長。

$C=2R\sin \left({\frac {\Delta }{2}}\right)\,\!$

視距特性

曲線視距受限

與直線平坦道路擁有很遠清晰的視線不同，水平曲線帶來了獨特的挑戰。曲線內側的自然地形，例如樹木、懸崖或建築物，如果離道路太近，可能會阻擋駕駛員對前方道路的視線。因此，可接受的設計速度通常會降低，以應對視距限制。

計算給定曲線可接受視距時存在兩種情況。第一種情況是視距被確定為小於曲線長度。第二種情況是視距超過曲線長度。每種情況都有各自的公式，根據幾何特性得出視距。確定哪種情況是正確的，通常需要對兩者進行測試，以找出哪一個是真實的。

給定某個視距$S$和已知的曲線長度$L$和內車道中心線半徑$R_{v}$，視距障礙物可以離道路內緣的距離$M_{s}$可以根據以下公式計算。

$S<L:M_{s}=R_{v}\left({1-\cos {\frac {28.65S}{R_{v}}}}\right)\,\!$

$S>L:M_{s}=R_{v}\left({1-\cos {\frac {28.65L}{R_{v}}}}\right)+\left({\frac {S-L}{2}}\right)\sin \left({\frac {28.65L}{R_{v}}}\right)\,\!$

演示

• Flash 動畫：路邊淨空區（Karen Dixon 和 Thomas Wall 製作）
• Flash 動畫：超高（Karen Dixon 和 Thomas Wall 製作）

示例

示例 1：曲線半徑

問題

問題

一條彎曲的公路設計速度為 110 公里/小時。在一條水平曲線處，超高設定為 6.0%，側向摩擦係數為 0.10。確定提供安全車輛執行的最小曲線半徑。

示例

解決方案

$R={\frac {v^{2}}{g\left({e+f_{s}}\right)}}={\frac {{(110*{(1000/3600))}}^{2}}{9.8\left({.06+0.10}\right)}}=595\ meters\,\!$

示例 2：確定里程

問題

問題

一個水平曲線設計為半徑 600 米，已知切線長為 52 米。PI 位於里程 200+00。確定 PT 的里程。

示例

解決方案

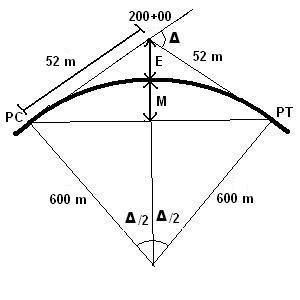本問題已知資訊

$T=R\tan \left({\frac {\Delta }{2}}\right)\,\!$

$52=600\tan \left({\frac {\Delta }{2}}\right)\,\!$

${\Delta }=9.9\deg \,\!$

$L={\frac {R\pi \Delta }{180}}={\frac {600\pi 9.9}{180}}=104\,\!$

$PC=PI-T=200+00\ -\ 0+52\ =199+48\,\!$

$PT=PC+L=199+48\ +\ 1+04\ =200+52\,\!$

示例 3：停車視距

問題

問題

一條單向賽道上非常長的水平曲線，其中心線半徑為 1750 米，兩條車道寬 4 米，設計車速為 200 公里/小時。確定從賽道內側邊緣到觀眾可以停車的最近距離，而不會阻礙駕駛員所需的視距。假設視距小於曲線的長度，摩擦係數為 0.3，感知反應時間為 2.5 秒。

示例

解決方案

中心線半徑為 1750 米，內側車道中心線距離頂點 1748 米（1750 - (4/2)）。使用停車視距公式（參見 視距），計算得 SSD 為 664 米。由此，可以很容易地找到觀眾可以停車的位置距離賽道的距離。

$S<L:M_{s}=R_{v}\left({1-\cos {\frac {28.65S}{R_{v}}}}\right)=1748\left({1-\cos {\frac {28.65(664)}{1748}}}\right)=31.43\ meters\,\!$

這得出了到內側車道中心的距離（31.43 米）。減去一半的車道寬度（在本例中為 2 米）即可得到到賽道邊緣的距離，即 29.43 米。

示例問題

問題 (解答)

演示

• 影片：水平線形、水平過渡和超高

其他問題

• 作業
• 其他問題

變數

• $R$ - 中心線曲線半徑
• $D_{a}$ - 曲線度 [水平曲線 30.5 米（100 英尺）弧長所對應的角度
• $T$ - 切線長（以長度單位表示）
• $\Delta$ - 曲線切線的偏轉角。 也是曲線的中心角，以度為單位。
• $E$ - 外部。 曲線與PI之間的最小距離
• $M$ - 中垂線
• $L$ - 曲線長度
• $C$ - 弦長
• $S$ - 視距
• $M_{s}$ - 可接受的視線障礙物放置在道路內緣的距離，不會阻礙視線距離
• $R_{v}$ - 最內側車道中心線的半徑

關鍵術語

• PC: 曲線起點
• PI: 切線交點
• PT: 切線終點