|
此模組可能需要完全重寫以適合其目標受眾。
你可以幫助重寫它。請檢視相關討論。 |
在本節中,我們將展示如何從三個線段構造一個三角形。構造基於第一卷,命題22
給定三個線段 ,
, 和
和 ,我們構建一個邊長等於這些線段的三角形。
,我們構建一個邊長等於這些線段的三角形。
- 複製直線
 到點A。
到點A。
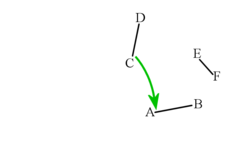
如果你忘記了如何操作,請遵循上一節的說明。你的構造應該看起來像下圖中的灰色線。將新線稱為

現在最好擦除你的輔助線,這樣就只剩下下面顯示的四條線段。

- 複製直線
 到點B。
到點B。
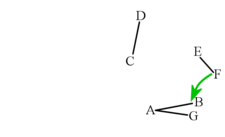
你的構造應該看起來像下圖中的灰色線。將新線稱為

- 畫圓
 ,其圓心為A,半徑為
,其圓心為A,半徑為 。
。
- 畫圓
 ,其圓心為B,半徑為
,其圓心為B,半徑為 。
。
- 設J為
 和
和 的交點。
的交點。

- 畫一條線
 .
.
- 畫一條線
 .
.
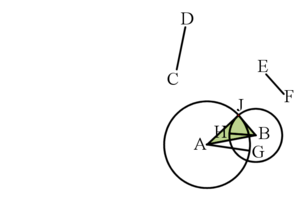
三角形  的邊分別等於
的邊分別等於  ,
,  和
和  .
.
- 線段
 是三角形的邊,等於它本身。
是三角形的邊,等於它本身。
- 線段
 等於
等於  ,因為它們都是圓
,因為它們都是圓 的半徑。並且因為它是複製的,所以
的半徑。並且因為它是複製的,所以 =
= 。因此
。因此  也等於
也等於 
- 線段
 等於
等於  ,因為它們都是圓
,因為它們都是圓  的半徑。並且由於它是複製的,
的半徑。並且由於它是複製的, =
= 。因此,
。因此, 也等於
也等於 
- 因此,三角形
 的邊分別等於
的邊分別等於  、
、 和
和  。
。
- 畫一條線
 ,長度隨意。
,長度隨意。
- 複製這條線
 到任意點 C,得到
到任意點 C,得到  。
。
- 畫一條線
 ,使其長度為
,使其長度為  長度的三倍。(我們沒有指定如何構建這樣的線段,留作練習。參考章節 複製線段 來解決。)
長度的三倍。(我們沒有指定如何構建這樣的線段,留作練習。參考章節 複製線段 來解決。)
- 用
 、
、 和
和  構造一個三角形。
構造一個三角形。
我們在測試中無法構建三角形的原因是,我們構造的圓圈沒有相交。不能用任意三條線段來構造三角形。線段的長度必須滿足一個稱為“三角形不等式”的條件。三角形不等式指出,任何一條線段都應小於另外兩條線段長度的總和。如果其中一條線段更長,則圓圈就不會相交。如果一條線段等於另外兩條線段的總和,我們會得到一條直線而不是三角形。
因此,構造是正確的,但應該對可以應用構造的線段進行條件限制。請注意,原始構造是歐幾里得提出的,因此構造或其證明中不存在錯誤。
























