遊戲開發指南/理論/數學/向量

3D 向量的示例

符號

向量用於儲存變數的多個分量，通常是空間維度的軸。因此，它們通常用於 2D 或 3D。

實際上，有兩種方法可以表示向量

2D

這可以定義為“旋轉和大小”或“x 方向上的位移和 y 方向上的位移”。

3D

這可以定義為“xz 方向上的旋轉、y 方向上的旋轉和大小”或“x 方向上的位移、y 方向上的位移和 z 方向上的位移”。

通常，在遊戲中，我們使用維度上的位移版本，而不是大小和旋轉。

向量可以有多種形式

i、j、k 形式 - 其中 i 表示 x 軸 上的 1 個單位，j 表示 y 軸 上的 1 個單位，如果是在 3D 中，k 表示 z 軸 上的 1 個單位

在 2D 中，它看起來像這樣：$3i+4j$，其中 3 表示 正 x 軸 上的 3 個單位，4 表示 正 y 軸 上的 4 個單位。

在 3D 中，它看起來像這樣：$6i-3j+5k$，其中 6 表示 正 x 軸 上的 6 個單位，-3 表示 負 y 軸 上的 3 個單位，5 表示 正 z 軸 上的 5 個單位。

列向量 - 這是最常見的向量形式。

在 2D 中，它看起來像這樣：${\begin{pmatrix}3\\4\end{pmatrix}}$，其中 3 表示 正 x 軸 上的 3 個單位，4 表示 正 y 軸 上的 4 個單位。

在 3D 中，它看起來像這樣：${\begin{pmatrix}6\\-3\\5\end{pmatrix}}$，其中 6 表示 正 x 軸 上的 6 個單位，-3 表示 負 y 軸 上的 3 個單位，5 表示 正 z 軸 上的 5 個單位。

行向量 - 這是最不常見的向量形式。

在 2D 中，它看起來像這樣：${\begin{pmatrix}3&4\end{pmatrix}}$，其中 3 表示 正 x 軸 上的 3 個單位，4 表示 正 y 軸 上的 4 個單位。

在 3D 中，它看起來像這樣：${\begin{pmatrix}6&-3&5\end{pmatrix}}$，其中 6 表示 正 x 軸 上的 6 個單位，-3 表示 負 y 軸 上的 3 個單位，5 表示 正 z 軸 上的 5 個單位。

在寫向量時，你可以用這種方式表示它

${\overrightarrow {V}}$ 或只是 ${\textbf {V}}$

從一個位置到另一個位置（從 A 到 B）時，可以這樣寫

${\overrightarrow {AB}}$

向量加減法

加向量就像加同類項一樣簡單。

加法

${\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}+{\begin{pmatrix}x_{2}\\y_{2}\\z_{2}\end{pmatrix}}={\begin{pmatrix}x_{1}+x_{2}\\y_{1}+y_{2}\\z_{1}+z_{2}\end{pmatrix}}$

減法

${\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}-{\begin{pmatrix}x_{2}\\y_{2}\\z_{2}\end{pmatrix}}={\begin{pmatrix}x_{1}-x_{2}\\y_{1}-y_{2}\\z_{1}-z_{2}\end{pmatrix}}$

注意：將常數加減到向量中是未定義的。

向量與常數的乘除（標量倍數）

當一個常數乘以/除以一個向量時，你只需將該乘以/除以操作應用於向量的所有分量。

乘法

$c{\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}={\begin{pmatrix}cx_{1}\\cy_{1}\\cz_{1}\end{pmatrix}}$

除法

${\frac {\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}{c}}={\frac {1}{c}}{\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}={\begin{pmatrix}{\frac {x_{1}}{c}}\\{\frac {y_{1}}{c}}\\{\frac {z_{1}}{c}}\end{pmatrix}}$

當一個向量乘以另一個向量時，有兩種定義的向量乘法方式：向量點積 和 向量叉積。

單位長度向量

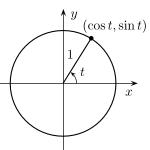二維中的單位向量基於此，這意味著x和y不能同時為1，否則它將不會形成一個圓，而是形成一個正方形，並且大小將大於1（一個單位）。

當大小不重要，只有方向重要時，使用單位向量。在二維中，它基於單位圓，在三維中，它基於單位球；x、y和z的值介於-1和1之間。

它的表示法是：${\hat {\textbf {V}}}$

要將向量轉換為單位長度向量，請使用以下公式：${\hat {\textbf {V}}}={\frac {\overrightarrow {\textbf {V}}}{{\Big |}{\overrightarrow {\textbf {V}}}{\Big |}}}$，這被稱為歸一化向量。

零向量

零向量（有時稱為零向量）是一個所有內容都是 0 的向量。如果零向量用 ${\overrightarrow {V}}$ 表示；

... 並且它在 2D 中，它看起來像：${\overrightarrow {V}}={\begin{pmatrix}0\\0\end{pmatrix}}$

... 並且它在 3D 中，它看起來像：${\overrightarrow {V}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}$

... 並且它在 $N$D 中，它看起來像：${\overrightarrow {V}}={\begin{pmatrix}0\\0\\\vdots \\0\end{pmatrix}}$

零位置向量的示例是原點；這是因為它有一個原點 $(0,0)$ 或 $(0,0,0)$。

另一個示例是，如果您想停止物體移動，您可以將 速度 設定為零向量。

大小

由於向量由許多部分組成，因此用於每個維度的數字表示每個方向的距離。為了找到對角線穿過維度的點到點的距離，您需要找到向量的模。

二維向量的模由（根據勾股定理）給出

$|{\overrightarrow {V}}|={\sqrt {V_{x}^{2}+V_{y}^{2}}}$

三維向量的模由給出

$|{\overrightarrow {V}}|={\sqrt {V_{x}^{2}+V_{y}^{2}+V_{z}^{2}}}$

位置向量

位置向量是一個被視為座標的向量，因此它是一個從原點到點的向量。字母O 通常用於表示原點。

位置向量可以寫成

${\overrightarrow {OA}}$

${\overrightarrow {OA}}={\begin{pmatrix}1\\0\\-3\end{pmatrix}}$ 等同於說有一個點 $A$，其座標為：$(1,0,-3)$

計算兩個位置向量之間的向量

${\overrightarrow {ba}}={\overrightarrow {a}}-{\overrightarrow {b}}$

${\overrightarrow {AB}}={\overrightarrow {OB}}-{\overrightarrow {OA}}$

${\overrightarrow {BA}}={\overrightarrow {OA}}-{\overrightarrow {OB}}$

練習：找出這些位置向量之間的向量 已知 ${\overrightarrow {OA}}={\begin{pmatrix}1\\0\\-3\end{pmatrix}}$ 和 ${\overrightarrow {OB}}={\begin{pmatrix}3\\2\\7\end{pmatrix}}$，求 ${\overrightarrow {AB}}$ 答案 ${\overrightarrow {AB}}={\begin{pmatrix}3\\2\\7\end{pmatrix}}-{\begin{pmatrix}1\\0\\-3\end{pmatrix}}$ ${\overrightarrow {AB}}={\begin{pmatrix}2\\2\\10\end{pmatrix}}$

點積

點積有兩個公式

${\overrightarrow {A}}\cdot {\overrightarrow {B}}=|{\overrightarrow {A}}||{\overrightarrow {B}}|\cos(\theta )$ 其中 $\theta$ 是兩個向量之間的夾角。

${\overrightarrow {A}}\cdot {\overrightarrow {B}}={\overrightarrow {A_{x}}}{\overrightarrow {B_{x}}}+{\overrightarrow {A_{y}}}{\overrightarrow {B_{y}}}+{\overrightarrow {A_{z}}}{\overrightarrow {B_{z}}}$

兩個向量的夾角

從這些公式，我們可以得到另一個計算它們之間夾角的公式

$\theta =\cos ^{-1}{\Bigg (}{\frac {{\overrightarrow {A}}\cdot {\overrightarrow {B}}}{|{\overrightarrow {A}}||{\overrightarrow {B}}|}}{\Bigg )}=\cos ^{-1}{\Bigg (}{\frac {{\overrightarrow {A_{x}}}{\overrightarrow {B_{x}}}+{\overrightarrow {A_{y}}}{\overrightarrow {B_{y}}}+{\overrightarrow {A_{z}}}{\overrightarrow {B_{z}}}}{|{\overrightarrow {A}}||{\overrightarrow {B}}|}}{\Bigg )}$

如果 ${\overrightarrow {A}}\cdot {\overrightarrow {B}}=0$，則這意味著這兩個向量是垂直的。

要注意的是 ${\overrightarrow {A}}\cdot {\overrightarrow {B}}={\overrightarrow {B}}\cdot {\overrightarrow {A}}$。

標量投影

標量投影

標量投影（或標量分量）是求一個向量（**A**）在另一個向量（**B**）上的投影的長度。

${\bigg |}proj_{\overrightarrow {B}}{\overrightarrow {A}}{\bigg |}=|{\overrightarrow {A}}|\cos \theta ={\frac {{\overrightarrow {A}}\cdot {\overrightarrow {B}}}{|{\overrightarrow {B}}|}}$

其中θ是**A**和**B**之間的夾角。

這個投影的向量（**A** 投影到 **B** 上）也可以用下面的公式求出

$proj_{\overrightarrow {B}}{\overrightarrow {A}}={\frac {{\overrightarrow {A}}\cdot {\overrightarrow {B}}}{|{\overrightarrow {B}}|^{2}}}{\overrightarrow {B}}$

向量方程

一個基本的向量方程由一個向量和另一個向量的變數係數組成。獨立的向量被稱為位置向量，而帶有變數係數的向量被稱為方向向量。位置向量表示向量在3D空間中的位置，而方向向量表示向量指向的方向。位置向量的向量可以是直線上任何點的的位矢。

一個典型的方程可能看起來像這樣: ${\textbf {r}}={\textbf {a}}+x{\textbf {b}}$ 或者 ${\textbf {r}}={\begin{pmatrix}2\\2\\2\end{pmatrix}}+x{\begin{pmatrix}1\\-2\\3\end{pmatrix}}$

檢查直線是否平行

當直線的方向向量是彼此的標量倍數時，這些直線是平行的。

示例

直線 1: ${\textbf {r}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+\lambda {\begin{pmatrix}1\\-2\\3\end{pmatrix}}$ 直線 2: ${\textbf {s}}={\begin{pmatrix}2\\5\\7\end{pmatrix}}+\mu {\begin{pmatrix}-2\\4\\-6\end{pmatrix}}$

它們是平行的，因為 $-2{\begin{pmatrix}1\\-2\\3\end{pmatrix}}={\begin{pmatrix}-2\\4\\-6\end{pmatrix}}$.

檢查一個點是否位於向量直線方程上

所以，如果該點的位置向量是 ${\textbf {P}}={\begin{pmatrix}2\\4\\4\end{pmatrix}}$，而直線方程是 ${\textbf {r}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\3\end{pmatrix}}$，並且你想看看 **P** 是否位於 **直線** 上，那麼你需要執行以下操作

將 **點** 等於 **方程**

${\begin{pmatrix}2\\4\\4\end{pmatrix}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\3\end{pmatrix}}$

從此你可以從每行建立 3 個獨立的方程

$2=1+2t$

$4=2+4t$

$4=3+3t$

然後解出每個方程以找到 **t**

$2=1+2t$ → $t={\frac {1}{2}}$

$4=2+4t$ → $t={\frac {1}{2}}$

$4=3+3t$ → $t={\frac {1}{3}}$

只有當所有 3 個 **t** 的值都相同時，**點** 才在 **直線** 上，因為其中一個 **t** 值與另外兩個不同，所以 **點** 不在 **直線** 上。

檢查兩個向量直線方程是否相交

因此，在這個例子中，你需要兩條直線，直線 1：${\textbf {r}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\2\end{pmatrix}}$ 和直線 2：${\textbf {s}}={\begin{pmatrix}4\\4\\2\end{pmatrix}}+u{\begin{pmatrix}1\\-2\\-3\end{pmatrix}}$

然後你需要將這兩個方程設為相等。

${\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\2\end{pmatrix}}={\begin{pmatrix}4\\4\\2\end{pmatrix}}+u{\begin{pmatrix}1\\-2\\-3\end{pmatrix}}$

然後減去一組常數以將常數保留在一側。

$t{\begin{pmatrix}2\\4\\2\end{pmatrix}}={\begin{pmatrix}3\\2\\-1\end{pmatrix}}+u{\begin{pmatrix}1\\-2\\-3\end{pmatrix}}$

由此，你可以從每一行建立一個方程

$2t=3+u$

$4t=2-2u$

$2t=-1-3u$

在找到 t 和 u 的值時，你只需要使用兩個方程，這樣你就可以檢查第三個方程是否匹配（在 2D 中不需要此檢查步驟）。我將使用方程 1 和方程 2： *使用任何你想要的聯立方程求解方法*

$2t=3+u$ → $4t=6+2u$ *將此方程的兩邊都乘以 2*

$4t=2-2u$

$0=4+4u$ *得到方程 1，並從中減去方程 2*

$u=-1$ 求解得到u

$4t=6+2(-1)$ 將u代回方程1

$t=1$ 求解得到t

現在讓我們檢查一下它是否適用於最終方程式，將u和t的值代入你沒有用過的方程式。

$2t=-1-3u$

$2(1)=-1-3(-1)$

$2=2$

如果你得到一個等式表示式（一個常數等於它自身），這意味著它們相交，否則它們不相交。這被稱為斜交。

直線方程上距離另一個點最近的點以及它們之間的距離

假設有一個向量方程${\textbf {r}}={\begin{pmatrix}2\\2\\2\end{pmatrix}}+t{\begin{pmatrix}1\\-2\\3\end{pmatrix}}$，並且有一個點P，其位置向量為：${\overrightarrow {OP}}={\begin{pmatrix}1\\1\\2\end{pmatrix}}$。我們想要找到直線上距離P最近的點的座標以及該點和P之間的距離。

我們將直線上的這個點稱為X。

首先，我們需要使用我們的點積規則，因為從P到X的直線將垂直於直線本身。為此，我們需要找到直線的方向和從P到X的向量。

直線的方向就是直線的方向向量（我們稱之為A）：${\textbf {A}}={\begin{pmatrix}1\\-2\\3\end{pmatrix}}$

至於P到X的方向，我們需要先找到X，即使它用t表示。

X就是直線方程本身寫成一個向量

${\overrightarrow {OX}}={\begin{pmatrix}2+t\\2-2t\\2+3t\end{pmatrix}}$

由此，我們可以使用“計算兩個位置向量之間的向量”找到用t表示的${\overrightarrow {PX}}$：

${\overrightarrow {PX}}={\overrightarrow {OX}}-{\overrightarrow {OP}}={\begin{pmatrix}2+t\\2-2t\\2+3t\end{pmatrix}}-{\begin{pmatrix}1\\1\\2\end{pmatrix}}={\begin{pmatrix}1+t\\1-2t\\3t\end{pmatrix}}$

現在我們有了兩個方向，就可以使用點積了

${\textbf {A}}\cdot {\overrightarrow {PX}}=0$

${\textbf {A}}_{x}{\overrightarrow {PX}}_{x}+{\textbf {A}}_{y}{\overrightarrow {PX}}_{y}+{\textbf {A}}_{z}{\overrightarrow {PX}}_{z}=0$

$1(1+t)-2(1-2t)+3(3t)=0$

$(1+t)(4t-2)+(9t)=0$

$14t-1=0$

$t={\frac {1}{14}}$

現在我們有了t的值，可以將其代入${\overrightarrow {OX}}$的方程式中

${\overrightarrow {OX}}={\begin{pmatrix}2+t\\2-2t\\2+3t\end{pmatrix}}={\begin{pmatrix}2+{\frac {1}{14}}\\2-2({\frac {1}{14}})\\2+3({\frac {1}{14}})\end{pmatrix}}={\begin{pmatrix}{\frac {29}{14}}\\{\frac {13}{7}}\\{\frac {31}{14}}\end{pmatrix}}$，這就是我們一直在尋找的位置向量（X）。

至於P和X之間的距離，我們需要將t代入我們的${\overrightarrow {PX}}$方程式中

${\overrightarrow {PX}}={\begin{pmatrix}1+t\\1-2t\\3t\end{pmatrix}}={\begin{pmatrix}1+{\frac {1}{14}}\\1-2({\frac {1}{14}})\\3({\frac {1}{14}})\end{pmatrix}}={\begin{pmatrix}{\frac {15}{14}}\\{\frac {6}{7}}\\{\frac {3}{14}}\end{pmatrix}}$

這是我們的向量，現在我們只需要找到向量的長度/大小

$|{\overrightarrow {PX}}|={\sqrt {{\overrightarrow {PX}}_{x}^{2}+{\overrightarrow {PX}}_{y}^{2}+{\overrightarrow {PX}}_{z}^{2}}}={\sqrt {{\bigg (}{\frac {15}{14}}{\bigg )}^{2}+{\bigg (}{\frac {6}{7}}{\bigg )}^{2}+{\bigg (}{\frac {3}{14}}{\bigg )}^{2}}}={\sqrt {{\frac {225}{196}}+{\frac {36}{49}}+{\frac {9}{196}}}}={\sqrt {\frac {27}{14}}}={\frac {3{\sqrt {42}}}{14}}$ ≈ $1.38873$, 這是 **點 P 到直線上最近點 X 的距離**。

叉積

叉積 (左), 右手定則 (右)

叉積定義為： ${\overrightarrow {A}}\times {\overrightarrow {B}}=|{\overrightarrow {A}}||{\overrightarrow {B}}|\sin(\theta ){\hat {n}}$，其中 $\theta$ 是 它們之間的夾角，而 ${\hat {n}}$ 是一個 單位向量，它同時垂直於 ${\overrightarrow {A}}$ 和 ${\overrightarrow {B}}$。叉積只在 3 維和 7 維中有效 (你不需要 7 維版本)。

有兩個向量同時垂直於 A 和 B，一個指向頁面/螢幕外，另一個指向螢幕內。一個是 ${\overrightarrow {A}}\times {\overrightarrow {B}}$，另一個是 ${\overrightarrow {B}}\times {\overrightarrow {A}}$。由於它們都指向不同的方向，並且大小相同，這意味著：${\overrightarrow {A}}\times {\overrightarrow {B}}=-{\overrightarrow {B}}\times {\overrightarrow {A}}$。你可以使用 右手定則 來找到叉積向量的方向。

由於你的電腦沒有 "右手"，你可以使用這個公式，它能做同樣的事情

${\overrightarrow {A}}\times {\overrightarrow {B}}={\overrightarrow {C}}={\begin{pmatrix}A_{y}B_{z}-A_{z}B_{y}\\A_{z}B_{x}-A_{x}B_{z}\\A_{x}B_{y}-A_{y}B_{x}\end{pmatrix}}$

法向量

法向量是一個指向幾何體表面向外的單位長度向量。對於每塊平面幾何體，存在兩個法向量，一個直接向上（相對於表面），另一個直接向下（相對於表面），使得一個與另一個相反。

計算法向量

要計算法向量，首先需要找到幾何體的一個角點。在該點處將有兩個邊延伸出來。你需要找到這兩條邊的向量。然後你需要找到邊 1 (E₁) 和邊 2 (E₂) 的叉積。之後你需要將向量歸一化使其單位長度。

${\overrightarrow {E_{1}}}\times {\overrightarrow {E_{2}}}={\overrightarrow {n_{1}}}$

${\hat {n_{1}}}={\frac {\overrightarrow {n_{1}}}{|{\overrightarrow {n_{1}}}|}}$

重寫成一個方程

${\hat {n_{1}}}={\frac {{\overrightarrow {E_{1}}}\times {\overrightarrow {E_{2}}}}{|{\overrightarrow {E_{1}}}\times {\overrightarrow {E_{2}}}|}}$

注意：從數學上來說，這更好，但在計算上更差，使用計算機時使用第一個版本來避免計算兩次叉積。這將需要儲存一個額外的變數，但對於處理器來說要容易得多。

要找到另一個法向量 (n₂)，可以使用以下任一方程

${\hat {n_{2}}}={\frac {{\overrightarrow {E_{2}}}\times {\overrightarrow {E_{1}}}}{|{\overrightarrow {E_{2}}}\times {\overrightarrow {E_{1}}}|}}$ 或者 ${\hat {n_{2}}}=-{\hat {n_{1}}}$

參見

• 在程式碼中建立 vector3 類

外部連結

• Khan Academy 關於叉積的影片，解釋右手定則：第一集 第二集
• Jorge Rodriguez 關於叉積的影片，包含計算機版本：https://www.youtube.com/watch?v=FT7MShdqK6w