高中三角學/三角形中的角

三角學這個詞源於兩個希臘詞，分別表示“三角形”和“度量”。正如你將在本章中學習的那樣，三角學涉及角度的測量，無論是三角形中的角度，還是旋轉中的角度（例如，像時鐘的指標一樣）。鑑於角度在三角學研究中的重要性，在本課中，我們將回顧三角形及其角度的一些重要方面。我們將從對不同型別的三角形進行分類開始。

學習目標

根據邊和角對三角形進行分類。
使用三角形內角和定理確定三角形中角的度數。
確定三角形是否相似。
使用相似三角形解決問題。

三角形及其內角

從形式上講，三角形定義為一個3邊形。這意味著三角形有3條邊，所有邊都是（直的）線段。我們可以根據邊或根據角對三角形進行分類。下表總結了不同型別的三角形。

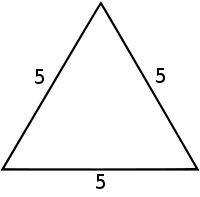
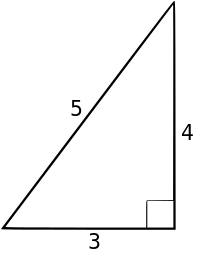
表 1.6：三角形的型別
名稱	描述	注意
等邊/等角	一個三角形，它有3條相等的邊和3個全等的角。	這種型別的三角形是銳角三角形
等腰	一個三角形，它有兩條相等的邊和兩個相等的角。	等邊三角形也是等腰三角形。
不等邊	一個三角形，它沒有成對的相等邊。
直角	一個三角形，它有一個90°角。	一個三角形不可能有多於一個90°角（見下文）。
銳角	一個三角形，它所有的三個角的度數都小於90°。
鈍角	一個三角形，它有一個角大於90°。	一個三角形不可能有多於一個鈍角（見下文）。

在下面的例子中，我們將對特定三角形進行分類。

例 1

確定哪個類別最能描述三角形

a. 邊長分別為 3、7 和 8 的三角形。

b. 邊長分別為 5、5 和 5 的三角形。

c. 邊長分別為 3、4 和 5 的三角形。

解:

a. 這是一個不等邊三角形。

b. 這是一個等邊或等角三角形。它也是銳角三角形。

c. 這是一個不等邊三角形，但它也是一個直角三角形。

雖然有不同型別的三角形，但所有三角形都有一點共同之處：三角形內角的和始終為 180°。如果你還記得一條直線構成一個“平角”，度數為 180°，那麼你會明白為什麼這是真的。現在考慮下面的圖，它顯示了三角形 *ABC*，以及透過頂點 *B* 畫的一條平行於邊 *AC* 的線。圖下方是三角形內角和的證明。

如果我們將邊 *AB* 和 *CB* 視為平行線之間的橫截線，那麼我們可以看到角 A 和角 1 是內錯角。
同樣，角 *C* 和角 2 是內錯角。
因此，角 *A* 和角 1 全等，角 *C* 和角 2 全等。
現在注意角 1、2 和 *B* 構成一條直線。因此，三個角的和為 180°。
我們可以使用替換完成證明

m\angle 1+m\angle B+m\angle 2=180

m\angle A+m\angle B+m\angle C=180

我們可以利用這個結果來確定三角形中角的度數。特別地，如果我們知道兩個角的度數，我們總是可以找到第三個角。

例 3

找出缺失角的度數。

a. 一個三角形有兩個角，分別為 30° 和 50°。

b. 一個直角三角形有一個角為 30°。

c. 一個等腰三角形有一個角為 50°。

解:

a. 100°

180 - 30 - 50 = 100

b. 60°

該三角形是一個直角三角形，這意味著一個角為 90°。

所以我們有：180 − 90 − 30 = 60

c. 50° 和 80°，或 65° 和 65°

有兩種可能性。首先，如果第二個角為 50°，則第三個角為 80°，因為 180 − 50 − 50 = 80。

在第二種情況下，50°角不是全等角之一。在這種情況下，另外兩個角的和為 180 − 50 = 130。因此，這兩個角分別為 65°。

請注意，關於三角形角度的資訊並不能告訴我們邊的長度。例如，兩個三角形可能具有相同的三個角，但這兩個三角形並不全等。也就是說，對應邊和對應角的度數並不相同。但是，這兩個三角形將是相似的。接下來，我們將定義相似性並討論三角形相似的條件。

相似三角形

考慮這樣一種情況：兩個三角形有三個對全等的角。

這些三角形是相似的。這意味著對應角全等，對應邊成比例。在上圖所示的三角形中，我們有以下內容

三對全等角
$\angle A\cong \angle D,\angle B\cong \angle E{\text{and }}\angle C\cong \angle F$
一個三角形內部邊的比率等於第二個三角形內部邊的比率
${\tfrac {\overline {AB}}{\overline {BC}}}={\tfrac {\overline {DE}}{\overline {EF}}},{\tfrac {\overline {AB}}{\overline {AC}}}={\tfrac {\overline {DE}}{\overline {DF}}},{\text{and }}{\tfrac {\overline {AC}}{\overline {BC}}}={\tfrac {\overline {DF}}{\overline {EF}}}$
對應邊的比例相等
${\tfrac {\overline {AB}}{\overline {DE}}}={\tfrac {\overline {BC}}{\overline {EF}}},{\tfrac {\overline {AB}}{\overline {DE}}}={\tfrac {\overline {AC}}{\overline {DF}}},{\text{and }}{\tfrac {\overline {BC}}{\overline {EF}}}={\tfrac {\overline {AC}}{\overline {DF}}}$

示例4

在上面的三角形中， ${\overline {AB}}=8,{\overline {BC}}=7,{\overline {AC}}=5,{\text{and }}{\overline {DE}}=4$ 。 DF 和 EF 的長度是多少？

解:

因為 ${\tfrac {\overline {AB}}{\overline {DE}}}={\tfrac {\overline {BC}}{\overline {EF}}}$ ，所以 ${\tfrac {8}{4}}={\tfrac {7}{EF}}\Rightarrow 2={\tfrac {7}{EF}}\Rightarrow 2EF=7\Rightarrow EF={\tfrac {7}{2}}=3.5$ 。

類似地，因為 ${\tfrac {\overline {AB}}{\overline {DE}}}={\tfrac {\overline {AC}}{\overline {DF}}}$ ，所以 ${\tfrac {8}{4}}={\tfrac {5}{EF}}\Rightarrow 2={\tfrac {5}{EF}}\Rightarrow 2EF=5\Rightarrow EF={\tfrac {5}{2}}=2.5$ 。

回顧一下，這些三角形被認為是相似的，因為它們有三個相等的角。這只是確定兩個三角形相似的三種方法之一。下表總結了確定兩個三角形相似的標準。

表 1.7：相似三角形的標準
標準	描述	示例
AAA	如果兩個三角形的三對角對應相等，那麼這兩個三角形相似。
SSS	如果兩個三角形的三對對應邊成比例，那麼這兩個三角形相似。
SAS	如果兩個三角形的兩對對應邊成比例，並且夾角相等，那麼這兩個三角形相似。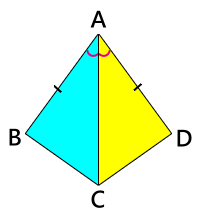

SSS 的一個特例是“HL”，即“斜邊-直角邊”。這是兩個直角三角形相似的情況。這種情況將在下面的示例 5 中進行研究。

示例 5

確定這兩個三角形是否相似。

解:

這兩個三角形相似。

回想一下，對於每個直角三角形，我們可以使用勾股定理來找到缺失邊的長度。在三角形 ABC 中，我們有

(AC)² + 8² =	10²
(AC)² + 64 =	100
(AC)² =	36
AC =	6

類似地，在三角形 DEF 中，我們有

(DF)² + 4² =	5²
(DF)² + 16 =	25
(DF)² =	9
DF =	3

因此，這兩個三角形的邊成比例，比例為 2:1。

因為我們總是可以這樣使用勾股定理，所以如果一個三角形的斜邊和一條直角邊與另一個三角形的斜邊和一條直角邊成比例，則這兩個直角三角形相似。這就是 HL 準則。

相似三角形的應用

相似三角形可以用來解決長度或距離成比例的問題。下面的例子將向你展示如何解決這類問題。

示例 6

使用相似三角形解決以下問題：

一棵樹的影子長 24 英尺。一個身高 5 英尺的人站在樹前面，他的影子長 8 英尺。這棵樹大約有多高？

解:

這幅圖顯示了兩個相似的直角三角形：人及其影子是其中一個三角形的兩條直角邊，樹及其影子是另一個三角形的兩條直角邊。這兩個三角形相似，因為它們的角：它們都有一個直角，並且它們共享一個角。因此，第三個角也相等，這兩個三角形相似。

這兩個三角形的長度之比是 3:1。如果我們用 h 來表示樹的高度，我們有

{\frac {h}{24}}={\frac {5}{8}}\Rightarrow h=24\left({\frac {5}{8}}\right)=15ft.

課程總結

在本課中，我們回顧了三角形的關鍵方面，包括不同型別三角形的名稱、三角形內角和、相似三角形的判定條件。在最後一個例子中，我們使用相似三角形來解決一個關於未知高度的問題。總的來說，三角形對於解決這類問題很有用，但請注意，我們並沒有使用三角形的角度來解決這個問題。這種技術將是你將在本章後面解決的問題的重點。

值得思考的點

為什麼一個三角形不可能有兩個以上的直角？
為什麼一個三角形不可能有兩個以上的鈍角？
一個角的度數可以有多大？

複習題

三角形 ABC 是一個等腰三角形。如果邊 AB 長 5 英寸，邊 BC 長 7 英寸，那麼邊 AC 長多少？
直角三角形可以是鈍角三角形嗎？解釋一下。
一個三角形有一個角是 48°，另一個角是 28°。這個三角形的第三個角是多少度？
斷言：任何直角三角形中的兩個非直角都是互餘的。
(a) 解釋為什麼這個斷言是正確的。

(b) 使用這個斷言來找到下面三角形的第三個角的度數。
在三角形 DOG 中，角 O 的度數是角 D 的度數的兩倍，角 G 的度數是角 D 的度數的三倍。這三個角的度數是多少？
下面的三角形 ABC 和 DEF 相似。 ${\overline {DF}}$ 的長度是多少？
在上面的三角形 ABC 和 DEF 中，如果角 A 的度數是 30°，那麼角 E 的度數是多少？
確定這兩個三角形是否相似
(a)

(b)
一棟建築物的影子長 100 英尺，而建築物旁邊的一根 20 英尺高的旗杆的影子長 24 英尺。這棟建築物有多高？
用你自己的語言解釋一下三角形相似意味著什麼。

答案

5 英寸或 7 英寸。
直角三角形不能是鈍角三角形。如果一個三角形是直角三角形，那麼它有一個角是 90 度。如果一個三角形是鈍角三角形，那麼它有一個角大於 90 度。因此，這兩個角的和將大於 180 度，這是不可能的。
104°
(a) 三角形內角和為 180 度。如果你減去 90 度的角，你將得到 180 - 90 = 90 度，這是剩餘兩個角的和。

(b) 90 - 23 = 67°
$m\angle D=36^{\circ }$
$m\angle O=72^{\circ }$
$m\angle G=108^{\circ }$
7.5
130°
(a) 否

(b) 是，根據 SSS 或 HL
83 ${\tfrac {1}{3}}$ 英尺
答案可能不同。答案應該包括 (1) 三對相等的角和 (2) 成比例的邊，或者其他關於“放大”或“縮小”的概念。

詞彙

銳角: 銳角的度數小於 90 度。
全等: 如果兩個角的度數相同，那麼這兩個角全等。如果兩條線段的長度相同，那麼這兩條線段全等。
銳角三角形: 所有角都是銳角的三角形。
等腰三角形: 有兩條邊相等，因此有兩個角相等的三角形。
等邊三角形: 三條邊都相等，因此三個角都相等的三角形。
不等邊三角形: 沒有一對邊相等的三角形。
直角邊: 直角三角形中較短的兩條邊之一。
斜邊: 直角三角形中最長的邊，與直角相對。
鈍角: 度數大於 90 度的角。
平行線: 永遠不會相交的直線。
直角: 度數為 90 度的角。
橫截線: 與平行線相交的直線。

← 基本函式 · 測量旋轉 →

本材料改編自可在此處找到的原始 CK-12 圖書。該作品根據知識共享署名-相同方式共享 3.0 美國許可協議授權。