高中三角函式/基本函式

本章將向您介紹一個特殊的函式族——三角函式，它是本書的基礎。在本第一課中，我們將回顧一般函式的基本特徵：什麼是函式，函式的圖形是什麼樣的，以及幾個函式族的特徵。雖然本課不會定義三角函式，但我們將考慮它們的基本特徵之一，以及這些函式的一些重要應用。

學習目標

確定一個關係是否為函式。
說明函式的定義域和值域。
根據函式族對函式進行分類。
識別函式的關鍵特徵，包括週期函式的概念。

函式的基礎

考慮下面方框中所示的兩種情況

情況1：您的汽車以 55 英里/小時的速度行駛，每加侖汽油可以行駛 30 英里。您每增加一英里/小時的速度，汽車每加侖汽油的行駛里程就會減少半英里。

情況2：您從您班上的幾位學生那裡收集了他們的年齡和身高（英寸）資料

年齡	18	17	18	18	17
身高	65"	64"	67"	68"	66"

在第一種情況下，令變數x表示汽車的速度，令y表示汽車使用一加侖汽油可以行駛的英里數。如果您以x英里/小時的速度行駛，那麼您將在一加侖汽油的驅動下行駛y = 30 − .5 (x − 55)英里。例如，如果您以 60 英里/小時的速度行駛，那麼您將在一加侖汽油的驅動下行駛 30 − .5(60 − 55) = 27.5 英里。請注意，您可以使用您的速度來“預測”一加侖汽油可以行駛多遠。

現在考慮第二種情況。您可以使用這些資料來“預測”身高，前提是知道學生的年齡嗎？

在第二種情況下並非如此。例如，如果一名學生 18 歲，那麼該學生可能有多種身高。

這兩種情況都是關係。關係僅僅是兩組數字或資料之間的關係。例如，在第二種情況下，我們透過將每個學生的資料寫成有序對，建立了學生年齡和身高之間的關係。在第一種情況下，汽車的速度與其一加侖汽油的使用效率之間存在關係。第一個例子與第二個例子不同，因為它表示一個函式：每個 x 只與一個 y 配對。一些關係在數學上很重要。例如，圓和橢圓是x和y座標之間重要關係的圖形表示，但對於每個x座標，並非都有唯一的y座標。由於每個x都有唯一的y，因此函式在數學和科學中發揮著重要作用。

我們可以用多種方式表示函式。一些最常見的表示函式的方式包括：有序對集、方程和圖形。下圖顯示了用每種表示法描繪的函式

表 1.1：函式示例
表示法	示例
有序對集	(1,3), (2,6), (3,9), (4,12)（此函式的有序對子集）
方程	y = 3x
圖形	y=3x

相反，下圖所示的關係不是函式

表 1.2：非函式示例
表示法	示例
有序對集	(4,2), (4,-2), (9,3), (9,-3)（此函式的有序對子集）
方程	x = y²
圖形	x=y^2

為了驗證此關係不是函式，我們必須證明至少有一個x值與多個y值配對。如果您檢視第一個表示法（有序對集），您可以看到 4 與 2 和 -2 配對。同樣，9 與 3 和 -3 配對。因此，該關係不是函式。如果我們檢視上面的圖形，我們可以看到，除了x = 0之外，關係的x值都與兩個y值配對。因此，上述關係不是函式。

快速確定一個關係是否為函式的一種方法是執行垂直線測試，這意味著您在圖形上畫一條垂直線。例如，如果我們在x = y²的圖形上畫一條x = 4的線，則該線將與圖形相交兩次。這意味著該關係不是函式。

示例1

確定關係是否為函式。

a. (2,4), (3,9), (5,11), (5,12)

b.

解答:

a. 此關係不是函式，因為 5 與 11 和 12 配對。如果您繪製這些點，則x = 5的線將與關係中的 2 個點相交。

b. 此關係是函式，因為每個x都只與一個y配對。

一旦您能夠確定一個關係是否為函式，那麼您應該能夠說明定義函式的x值集和y值集。

函式的定義域定義為函式定義的所有x值的集合。例如，函式y = 3x的定義域是所有實數的集合，通常寫成 $\mathbb {R}$ 。這意味著x可以是任何實數。其他函式具有受限的定義域。例如，函式 $y={\sqrt {x}}$ 的定義域是所有大於或等於零的實數的集合。此函式的定義域之所以受到限制，是因為負數的平方根不是實數。因此，定義域被限制為非負的x值，以便函式值被定義。

通常可以透過 (1) 考慮可能存在的限制和 (2) 檢視圖形來輕鬆確定函式的定義域。

示例2

說明每個函式的定義域。

a. y = x²

b. $y={\tfrac {1}{x}}$

c. (2, 4), (3, 9), (5, 11)

解答:

a. 此函式的定義域是所有實數的集合。沒有限制。

b. 此函式的定義域是所有實數的集合，除了 x ≠ 0。定義域之所以受到此限制，是因為分母為零的分數是未定義的。

c. 此函式的定義域是x值的集合 {2, 3, 5}。

變數x通常稱為自變數，而變數y通常稱為因變數。我們這樣談論x和y，因為函式的y值取決於x值是什麼。這就是為什麼我們也說“y是x的函式”。例如，函式y = 3x中y的值取決於我們正在考慮的x值。如果x = 4，我們可以很容易地確定y = 3(4) = 12。

當我們使用方程形式的函式時，有一種特殊的符號可以用來強調y是x的函式這一事實。例如，方程y = 3x也可以寫成f(x) = 3x。務必記住，f(x)表示y值或函式值，字母f**不是**變數。也就是說，f(x)並不意味著我們將數字f乘以另一個數字x。可以將函式想象成一臺機器，它接收一個數字x，並輸出另一個數字。在表示式f(x)中，f是機器，括號()是輸入x進入機器的地方。f(x)是機器使用輸入x產生的輸出。例如，假設你的機器對輸入加5。那麼f(3) = 8，或者更一般地，f(x) = x + 5。

現在我們已經考慮了函式的定義域，我們將轉向函式的**值域**，它是函式定義的所有y值的集合。就像我們對定義域所做的那樣，我們可以檢查一個函式並確定它的值域。同樣，考慮可能存在的限制以及函式的圖形是什麼樣子通常很有幫助。例如，考慮函式y = x²。

此函式的值域是所有大於或等於零的實數的集合。這是因為每個y值都是一個x值的平方。如果我們對正數和負數進行平方，結果將始終為正。如果x = 0，則y = 0。如果我們檢視y = x²的圖形，我們也可以看到值域。

一些函式有突然的跳躍。考慮將數字舍入到最接近的整數的“舍入”函式（如果數字正好位於兩個整數之間，則向上舍入）。因此，此函式的一些值為 (2, 2)、(1.4, 1)、(3.9, 4)、(5.5, 6) 和 (−5.5, −5)。此函式的定義域是所有實數，但函式的值域是整數。

另一個跳躍函式來自出租車通常的收費方式。假設計程車前2英里收費5.00美元，然後每增加1英里或部分英里收費1美元。考慮一個函式，其中行駛距離作為輸入，計程車費作為輸出。因此，此函式的一些值為 (1, 5)、(1.9, 5)、(2.1, 6)、(10, 13)。此函式的定義域是非負實數（因為你不能乘坐計程車行駛負距離）。此函式的值域是所有大於或等於 5 的正整數：{5, 6, 7, 8, ...}。

示例 3

指出函式 $y={\tfrac {2}{x}}$ 的定義域和值域。

解答:

對於此函式，我們可以選擇任何x值，除了x ≠ 0。因此，函式的定義域是所有實數的集合，除了x ≠ 0。

值域也限於非零實數，但原因不同。因為分數的分子是2，所以分子永遠不可能等於零，因此分數永遠不可能等於零。

現在我們已經定義了關係是什麼是函式，並且我們已經定義了函式的定義域和值域，我們可以檢視一些特定函式及其圖形的示例。

函式族

我們迄今為止看到的示例包括幾種不同型別的函式。根據您之前使用方程和圖形的經驗，您可能已經對方程形式與圖形外觀之間的關係建立了聯絡。在這裡，我們將檢查幾個函式“族”。函式族是一組方程形式相似的函式。“母函式”是指族中最簡單的形式的方程。例如，y = x²是其他函式（如y = 2x² − 5x + 3）的母函式。下表總結了幾個函式族的關鍵方面。

表 1.3：函式族
函式族	母函式	關鍵方面
線性函式	y = x	線性函式的圖形是一條直線，通常根據其斜率和y截距來識別。直線的斜率是係數 ${\tfrac {1}{2}}$ ，y截距是常數 1。
二次函式	y = x²	這些函式的最高指數為 2。圖形是拋物線，它有一個頂點，該頂點是圖形的全域性最大值或最小值。頂點是點 (1, -1)。圖形關於直線x = 1 對稱。
三次函式	y = x³	這些函式的最高指數為 3。圖形的兩端具有相反的行為。三次函式的圖形要麼有一個區域性最大值和最小值，如右側圖形所示，要麼沒有區域性最大值或最小值，如y = x³。
指數函式	y = 2^x、y = 3^x 等。	指數函式的指數是變數。圖形具有水平漸近線。當x接近 $-\infty$ 時，函式值接近x軸 (y = 0)。
有理函式	$y={\tfrac {1}{x}},$ 等。	這些函式包含分子和分母中都有多項式的分數。圖形具有水平和垂直漸近線。當x接近 $\pm \infty$ 時，y值接近 0 (x軸)。當x接近 1 時，y值接近 $\pm \infty$ 。

所有這些函式都可以用來表示真實情況。例如，線性函式y = 3x在上面用於表示你銷售每塊 3.00 美元的糖果棒能賺多少錢。這種情況稱為**正比例關係**。我們說你賺的錢與你賣出的糖果棒的數量成正比。兩個變數之間的正比例關係將始終由形式為y = mx的線性函式建模。直線的斜率m是比例常數。請注意，直線的y截距為 0；也就是說，直線包含點 (0, 0)。從賣糖果的角度來看，這是有道理的：如果你賣 0 塊糖果棒，你就賺 0 美元。

其他情況可以用不同型別的線性函式建模。考慮以下情況：一家餐廳正在舉行促銷活動：一個大乳酪比薩餅 8.00 美元，每個配料 2.00 美元。比薩餅的成本可以用函式c(x) = 2x + 8 建模，其中x是比薩餅上的配料數量。直線的斜率為 2，因為每個配料都會使價格增加 2 美元。y截距為 8：如果你不選擇任何額外的配料，比薩餅的成本為 8.00 美元。

二次、三次和其他多項式函式可以用來模擬許多型別的情況。另一個重要的函式族是有理函式，或多項式的商，例如

f(x)={\frac {3x}{x^{2}+1}}

f(x)={\frac {1}{x}}

例如，可以使用有理函式來模擬兩個變數之間的反比例關係。反比例關係意味著兩個變數的乘積是常數：xy = k。如果我們解出此方程以求得y，則有 $y={\tfrac {k}{x}}$ ，這是一個有理函式。以下示例展示了實際情況中的反比例關係

示例 4

有時你開車上班，有時你騎腳踏車上班。昨天你以平均 40 英里/小時的速度開車，用了 15 分鐘。今天你以 20 英里/小時的速度騎腳踏車，用了半小時。

寫出一個方程，表示你的速度和你上班所需時間之間的關係。

解答:

y={\frac {10}{x}}

，其中x 是你的速度（英里/小時），y 是你上班所需的時間（小時）。

首先，請注意家和工作地點之間的距離為 10 英里

{\text{40 miles per hour}}\times {\frac {1}{4}}hr={\text{10 miles}}

{\text{20 miles per hour}}\times {\frac {1}{2}}hr={\text{10 miles}}

我們知道，一般來說

{\text{rate}}\cdot {\text{time}}={\text{distance}}

{\text{time}}={\frac {\text{distance}}{\text{rate}}}

因此，如果你以x 英里/小時的速度開車或騎車，那麼你上班需要y 小時： $y={\frac {10}{x}}$ 。

一般來說，函式可以用來模擬許多環境中的真實現象，包括科學、商業、經濟等不同領域。可以用來模擬特定情況的函式型別取決於函式的關鍵方面，這些關鍵方面將與情況的關鍵方面相匹配。許多情況的一個方面在我們迄今為止看到的函式型別中沒有體現，但將在本章中你將學習到的三角函式中體現。例如，考慮下表，它顯示了 1971 年至 2000 年馬薩諸塞州波士頓市每月平均最高和最低氣溫。（來源：rssweather.com）

表 1.4：馬薩諸塞州波士頓市的月平均最高/最低氣溫
月份	最低	最高
一月	22.1°F	36.5°F
二月	24.2°F	38.7°F
三月	31.5°F	46.3°F
四月	40.5°F	56.1°F
五月	50.2°F	66.7°F
六月	59.4°F	76.6°F
七月	65.5°F	82.2°F
八月	64.5°F	80.1°F
九月	56.8°F	72.5°F
十月	46.4°F	61.8°F
十一月	37.9°F	51.8°F
十二月	27.8°F	41.7°F

下圖顯示了平均低溫。

請注意，該圖包含一整年的資料，然後以 12 月（第 12 個月）結束。我們有可能用我們討論過的某個函式族中的函式來近似該圖所暗示的曲線。並非所有自然現象都能用數學函式建模，但許多都能。

假設此資料總體上代表了波士頓的天氣。我們可以建立一個函式，其輸入是從現在開始的月份時間，其輸出是預期的平均溫度。例如f(1) = 22.1，f(5) = 50.2。該函式將在一年後重複。13 代表什麼？根據這些資料，預計氣溫是多少？

由於月份每年迴圈，因此 13 代表下一年的 1 月，並且一般來說，我們可以根據我們對某個地點的通常氣候的瞭解來預測 1 月的天氣。例如，1 月是波士頓市一年中最冷的月份。在表格所示的年份中，平均低溫約為 22 度。因此，我們可以預測波士頓 1 月的平均低溫將約為 22 度。我們可以使用這樣的函式將當前天氣與過去的天氣進行比較，並檢驗隨時間推移的氣候變化。

由於一年中的月份和天氣模式本質上是迴圈的，因此我們需要用一個本質上也是迴圈的函式來模擬這種情況。此類函式稱為週期性函式。如果存在某個值p，使得對於函式域中的所有x，f(x + p) = f(x)，則該函式是週期性的。你將在本章中學習到的三角函式是一種週期性函式，我們可以使用某些三角函式來模擬上面顯示的天氣資料。我們將在本課結束時回到這個主題，但現在我們將看看函式的圖形。

函式繪圖和技術工具

雖然有一些技巧可以讓你高效地手繪許多函式的影像，但使用繪圖計算器可以讓你快速繪製任何函式的影像，並識別函式的關鍵特徵。以下兩個例子將向你展示如何使用TI圖形計算器來探索函式。

例5

繪製函式y = x³ − 3x² + 1 的影像

a. 當x = 0，x = 2 和 x = −2 時，計算函式值。

b. 描述函式的端點行為。

c. 近似所有x截距。

d. 近似任何區域性最大值和最小值。

解答:

要繪製此函式的影像，請按[Y=]，並清除已輸入的任何方程。在Y1中，輸入方程。如果你以前從未輸入過方程，這裡有一些提示

x 按鈕位於綠色[ALPHA]按鈕旁邊（在TI-83型號上）。
要將x 提升到3次方，請按[MATH].
要將x 提升到2次方，請按[x²]按鈕，該按鈕位於左側列。
小心使用負號：右側的藍色“−”按鈕用於減法。底部寫著“(−)”的按鈕用於表示負數。

輸入方程後，請按[ZOOM] [6]。這將帶你到“標準”視窗：你可以看到從−10到10的x和y。（注意，如果你向下滾動到選項6，則需要按回車鍵。但是，如果你只輸入數字6，則會進入圖形。）

a. 要計算函式值，你可以“跟蹤”圖形。按[TRACE]按鈕。你應該在螢幕頂部看到方程，游標應該位於y截距 (0, 1) 上。在螢幕底部，你應該看到x = 0 和y = 1。這告訴我們，對於x = 0，函式值為1。

現在你處於跟蹤模式，你可以輸入任何x值，計算器將告訴你y值。例如，如果你按下[2] [ENTER]，你會看到游標移動到點 (2,−3)，並且在螢幕底部，你會看到x = 2 和y = −3。如果你按下[(-)] [2] [ENTER]，你將在螢幕底部看到x = −2 和y = −19。請注意，你無法在圖形上看到該點。要檢視該點，我們需要更改視窗。按[WINDOW]並向下滾動到Ymin。將−10更改為−25。然後按[GRAPH]。現在按[TRACE] [(-)] [2] [ENTER]。你應該看到點(−2,−19)。

b. 端點行為：圖形的左側似乎正在向下，右側似乎正在向上。如果我們想看到更多圖形，我們可以縮小。按[ZOOM] [3]。這將增大視窗的大小。如果你按下[ENTER]，視窗將再次增大。如果你這樣做兩次，你會注意到軸看起來很粗，圖形很難看清。這是因為軸上的刻度設定為1。按[WINDOW]並向下滾動到Xscl。如果你按下[DELETE]，這將刪除所有刻度。（你也可以將刻度設定為更大的值。）為了更好地檢視圖形，你還可以減小Xmin和Xmax。將Xmin設定為−20，將Xmax設定為20。按[GRAPH]。現在你可以看到函數了。按[TRACE]向任一方向移動，你將能夠看到圖形的左側繼續向下，右側繼續向上。

c. x截距：要將圖形返回到較小的視窗，請按[ZOOM] [6]。如果你想在較小的視窗中檢視圖形，請按[ZOOM] [4]。你應該看到圖形有3個x截距。你可以透過跟蹤直觀地近似它們：按[TRACE]並將游標向左移動。最左邊的x截距大約為−0.5。要找到x截距的良好近似值，請按[2nd] [TRACE] [2]。這會將你送回圖形。在螢幕上，你將看到問題“左邊界？”將游標移動到x截距的左側。（在這種情況下，你將向下移動。）按[ENTER]。然後你將看到問題“右邊界？”將游標移動到x截距的右側，但不要移動太遠（不要超過下一個x截距。）按[ENTER]。然後將要求你“猜測”截距。將游標移回左側，儘可能靠近x截距。按[ENTER]。你應該看到x = −0.5320888。這是x截距的近似值。如果你使用相同的步驟，你會發現其他x截距大約為0.6527和2.879。

d. 最大值和最小值：請注意，圖形有一個“山峰”和一個“谷底”。山峰稱為“區域性最大值”，因為它是在某個區間內圖形上的最高點。谷底類似地稱為“區域性最小值”。要近似最大值的座標，請按[TRACE]並跟蹤靠近最大值的位置。看起來最大值是 (0, 1)。要驗證這一點，請按[2nd] [TRACE] [4]。要找到最大值，我們必須執行與查詢x截距時相同的“左邊界、右邊界、猜測”過程。此過程應告訴你最大值為 (0, 1)。（注意：x值可能顯示類似“9.64487E −7”的內容。這只是一個小的計算器誤差。此數字非常接近0！）要找到最小值，請跟蹤“谷底”。（如果需要，你可以轉到[WINDOW]並將Ymin設定為更小的數字，以便你可以清楚地看到圖形的最小值。）現在按[2nd] [TRACE] [3]。這會將你送回圖形。執行“左邊界、右邊界、猜測”過程應顯示最小點為 (2, −3)。

例6

你有100英尺長的柵欄，用來在穀倉旁邊圍一塊地。你希望圍成的地是矩形。

a. 寫出一個函式來模擬地塊面積與地塊寬度的關係。

b. 使用繪圖計算器繪製該函式的影像。

c. 你應該用柵欄圍成什麼尺寸的矩形才能使矩形圍欄的面積最大化？

d. 解釋x截距的意義。

解答:

地塊將如下圖所示

a. 方程：矩形地塊的面積是其長和寬的乘積。我們可以將面積寫成x的函式：A(x) = 2xh。如果我們考慮到我們有100英尺長的柵欄，並寫出一個關於我們如何使用這100英尺柵欄的方程，我們就可以從方程中消去h：x + 2h = 100。（由於穀倉的存在，矩形的第四邊不需要柵欄。）我們可以解出此方程以求得h，並將其代入面積方程

$x+2h=\,\!$	$100\Rightarrow 2h=100-x\Rightarrow h=50-{\frac {x}{2}}$
$A(x)=\,\!$	$2xh=2x\left(50-{\frac {x}{2}}\right)$
$A(x)=\,\!$	$100x-x^{2}\,\!$

b. 圖形：按[Y=]並清除任何方程。然後在Y1中輸入方程。請注意，如果你按下[ZOOM] [6]，你將看不到任何圖形。你可以透過按下[ZOOM] [3]來縮小，但根據函式值選擇視窗可能更有效。按[2nd] [WINDOW]

為了設定表格。TblStart 是您希望在表格中看到的第一個條目。Tbl 允許您設定增量。例如，如果您想看到x = 1、2、3、4 等，則將其設定為 1。對於此示例，將其設定為 10。確保 Indpnt 和 Depend（x 和 y）設定為“自動”。然後按[2nd] [GRAPH]查看錶格。如果滾動瀏覽表格，您會發現當x = 50 時，y 值達到 2500，然後值開始下降。現在我們可以設定視窗。按[WINDOW]。並將 Xmin 設定為 -1，Xmax 設定為 105，Ymin 設定為 -200，Ymax 設定為 3000。（注意：您可以將 Xmin 和 Ymin 分別設定為 0，但將它們設定為 -1 和 -200 可以讓您看到座標軸。）

A(x) 的圖形在此處顯示在區間 [0, 100] 上。

c. 最大可能面積：使用示例 6 中的方法，您應該會發現 (50, 2500) 是最大點。這告訴我們，當矩形的寬度為 50 英尺時，面積為 2500 平方英尺。

d. 截距：使用示例 5 中的方法，您應該會發現x 截距位於 0 和 100。這告訴我們，如果花園的寬度為 0，則面積為 0。如果土地的寬度為 100，則面積為 0。這是因為只有 100 英尺的柵欄。如果寬度為 100，則矩形的其餘部分沒有更多的柵欄了！

三角函式簡介

再次考慮上面提到的溫度資料

如上所述，這種資料需要用週期函式來建模。特別是，這種資料通常由正弦曲線建模，正弦曲線以特定的方式振盪，如下面的圖形所示。

每個正弦曲線都以規則的間隔重複其值。如果我們用這樣的圖形對天氣資料進行建模，則值將每 12 個月重複一次。因此，我們說該函式的週期為 12。

請注意，資料範圍約為 22 到 65。還要注意，“波浪”在這些值之間居中，大約在y = 43 處。因此，我們說波浪的振幅約為 21，即從中間到波浪頂部或底部的距離。

許多現實現象可以用這種函式來建模。

課程總結

在本課中，我們回顧了函式的概念，包括函式的主要方面和不同型別的函式。我們還使用了圖形計算器來繪製和探索不同的函式。本課的一個關鍵點是我們可以使用函式來模擬現實現象。第二個關鍵點是，為了模擬本質上是迴圈的現象，我們需要使用週期函式。在本章的第 4 課中，我們將定義六個三角函式。但是，由於這些函式的輸入是角度，所以在接下來的兩節課中，我們將重點關注角度。首先，我們將回顧幾何中的三角形角度，然後我們將考慮旋轉中的角度。

思考點

是什麼將函式與關係區分開來？
是什麼使函式具有周期性？
使用計算器繪製函式圖的優缺點是什麼？

複習題

確定每個關係是否為函式
(a) (−1, 4), (0, 3)(1, 5), (1, 7), (2, 15)

(b) y = 3 - x

(c)
一列火車以每小時 95 英里的恆定速度行駛。
(a) 寫出一個方程，表示火車行駛時間與行駛距離之間的關係。

(b) 這種情況是正比例關係、反比例關係還是都不是？

(c) 使用該方程確定火車在 3 小時後行駛的距離。
您決定開始一個小型企業，製作相框。您花費 100 美元購買油漆和其他用品，以及每個木製相框 2.00 美元。您決定以每個 10.00 美元的價格出售每個相框。
(a) 寫出一個線性函式來模擬您業務的成本。

(b) 寫出一個線性函式來模擬您業務的收入。（收入是您收到的金額。）

(c) 寫出一個線性函式來模擬您業務的利潤。（利潤可以透過從收入中減去成本來找到。）

(d) 使用您的利潤函式確定必須銷售的最低相框數量才能獲利。
考慮由方程f(x) = x² − x − 3 定義的函式。
(a) 此函式屬於哪個函式族？

(b) 說明該函式的定義域和值域。

(c) 使用圖形計算器繪製函式圖，以識別頂點的近似座標和x 截距的近似值。
考慮函式 $y={\tfrac {x-2}{x+3}}$
(a) 使用圖形計算器繪製函式圖。

(b) 識別所有漸近線。
在一間餐廳預訂一個私人派對房間的價格為 500 美元。每人的價格與參加派對的人數成反比。
(a) 寫出一個方程，表示每人成本 c 與參加人數 p 之間的關係。

(b) 如果有 32 人參加，使用該方程求出每人的成本。
使用圖形計算器繪製函式y = x³ + x、y = x³ + 2x、y = x³ − x 和y = x³ − 2x 的圖。改變第二項係數會產生什麼影響？
方程p(x) = −.5x² + 90x − 200 表示一家公司的利潤，其中 x 是該公司銷售的單位數量。使用圖形計算器繪製函式圖，並使用圖形回答問題。
(a) 最大利潤是多少，必須銷售多少單位才能達到最大利潤？

(b) 找到x 截距，並解釋這些點在圖形上的含義，即公司的利潤。
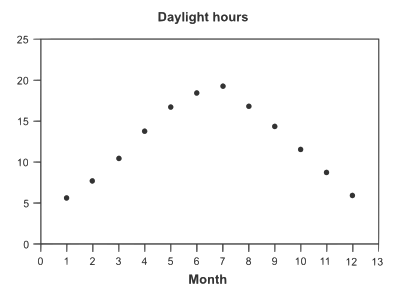
下表顯示了阿拉斯加安克雷奇每個月的平均日照時間。
(a) 使用圖形計算器繪製資料圖，或手工繪製圖。使用 1 月 = 1。

(b) 資料的週期是多少？

(c) 如果資料表示您居住地的日照時間，圖形可能會有何不同？

表 1.5
月份	平均日照時間
一月	5.65
二月	7.77
三月	10.4
四月	13.37
五月	16.87
六月	18.72
七月	19.18
八月	17.12
九月	14.27
十月	11.43
十一月	8.53
十二月	6.13

複習答案

(a) 不是函式

(b) 是函式

(c) 不是函式
(a) y = 95x

(b) 這種情況是正比例關係。

(c) 285 英里
(a) C(x) = 2x + 100

(b) R(x) = 10x

(c) P(x) = 8x - 100

(d) 您必須製作和銷售 13 個相框才能獲利。
(a) 這是一個二次函式。

(b) 定義域是所有實數的集合。值域是大於或等於 3.25 的所有實數的集合。

(c) 頂點：(0.5, -3.25)；x 截距：-1.3、2.3
(a)

(b) x = -3, y = 1
(a) $cp=500\quad {\text{or}}\quad c={\frac {500}{p}}\quad {\text{or}}\quad p={\frac {500}{c}}$

(b) 15.63 美元
當係數增大時，具有正係數的方程越來越像y = x³。具有負係數的方程具有區域性最大值和最小值。減小系數會增加“山峰”和“山谷”的大小。
(a) 最大利潤為 3,850 美元，銷售 90 個單位。

(b) 2.25 和 177.75。這些是盈虧平衡點。當銷售 2-3 個單位時，公司已賺取足夠的錢來彌補初始成本。在銷售 177 個單位後，公司不再盈利。
(a)

(b) 週期 = 12

(c) 在美國其他城市，日照時間變化不大。圖形的振幅會更小。

詞彙表

因變數: 函式的自變數，通常用x表示。
定義域: 定義域是函式定義的自變數 (x) 的集合。
函式: 一種關係，其中定義域的每個元素都與值域的恰好一個元素配對。
自變數: 函式的輸出變數，通常用y表示。
週期函式: 任何規律重複的函式。
值域: 函式的輸出值或函式值 (y) 的集合。
關係: 兩組數字或資料中的專案之間的配對。; 座標是圖或函式中的兩個點；

← 三角學與直角 · 三角形中的角 →

此材料改編自可在此處找到的原始 CK-12 圖書。此作品根據知識共享署名-相同方式共享 3.0 美國許可證授權。