高中三角學/直角三角形三角學應用

在本課中，我們將回到直角三角形三角學。許多現實情況都涉及直角三角形。在你之前學習幾何時，你可能已經使用直角三角形來解決涉及距離的問題，使用勾股定理。在本課中，你將使用你對角度和三角函式的知識，解決涉及直角三角形的問題。我們將首先解決直角三角形，這意味著要確定所有三個角的度數以及直角三角形所有三條邊的長度。然後我們將轉向幾種型別的問題。

學習目標

解直角三角形。
解決需要你解直角三角形的現實世界問題。

解直角三角形

你可以使用你對勾股定理和六個三角函式的知識來解直角三角形。因為直角三角形是一個帶有 90 度角的三角形，所以解直角三角形需要你找到另外一個或兩個角的度數。你如何解決將取決於提供的資訊量。以下示例展示了兩種情況：一個缺少一條邊的三角形，以及一個缺少兩條邊的三角形。

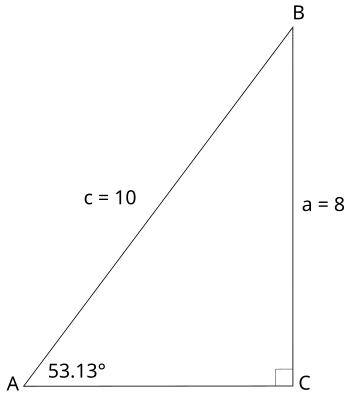
示例 1

解下圖所示的三角形。

解答:

我們需要找到所有邊的長度和所有角的度數。在這個三角形中，給出了三條邊中的兩條。我們可以使用勾股定理找到第三邊的長度

$8^{2}+b^{2}=\,\!$	$10^{2}\,\!$
$64+b^{2}=\,\!$	$100\,\!$
$b^{2}=\,\!$	$36\,\!$
$b=\,\!$	$\pm 6\Rightarrow b=6\,\!$

(你可能也認識到“勾股定理三元組”，6、8、10，而不是執行勾股定理本身。)

你也可以使用三角比找到第三邊。注意，缺失的邊，b，與角A相鄰，斜邊已知。因此，我們可以使用餘弦函式來找到b的長度

$\cos(53.13^{\circ })=\,\!$	${\frac {\text{adjacent side}}{\text{hypotenuse}}}={\frac {b}{10}}$
$0.6=\,\!$	${\frac {b}{10}}$
$b=\,\!$	$0.6(10)=6\,\!$

我們也可以使用正切函式，因為給出的是對邊。你可能覺得用多種方法來找到缺失的邊很混亂。然而，重點不是製造混亂，而是表明你必須檢視哪些資訊是缺失的，並選擇一種策略。總的來說，當你需要識別三角形的一條邊時，你可以使用勾股定理，或者使用三角比。

為了解決上述三角形，我們還需要確定所有三個角的度數。已知兩個角：90 度和 53.13 度。我們可以使用三角形內角和公式來找到第三個角。

180 − 90 − 53.13 = 36.87°

現在讓我們考慮一個有兩個邊缺失的三角形。

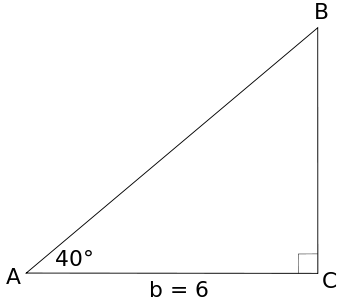
示例 2

解下圖所示的三角形。

解：在這個三角形中，我們需要找到兩條邊的長度。我們可以使用三角函式比來找到一條邊的長度。然後，我們可以使用三角函式比或勾股定理來找到第三條邊的長度。

我們已知角 A 的度數以及與角 A 相鄰的邊的長度。如果我們要找到斜邊的長度 c，我們可以使用餘弦比

$\cos(40^{\circ })=\,\!$	${\frac {\text{adjacent}}{\text{hypotenuse}}}={\frac {6}{c}}$
$\cos(40^{\circ })=\,\!$	${\frac {6}{c}}$
$c\cos(40^{\circ })=\,\!$	$6\,\!$
$c=\,\!$	${\frac {6}{\cos(40^{\circ })}}\approx 7.83$

如果我們要找到三角形另一條邊的長度，我們可以使用正切比。（為什麼這比使用正弦比更好？）

$\tan(40^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {a}{6}}$
$\tan(40^{\circ })=\,\!$	${\frac {a}{6}}$
$a=\,\!$	$6\tan(40^{\circ })\approx 5.03\,\!$

現在我們知道這個三角形所有三條邊的長度。在複習問題中，您將使用勾股定理驗證 c 和 a 的值。在這裡，為了完成三角形的求解，我們只需要找到角 B 的度數。

180 − 90 − 40 = 50°

請注意，在兩個示例中，兩個非直角中有一個是已知的。如果兩個非直角都沒有給出，您將需要新的策略來找到角度。您將在第 4 章學習這種策略。

仰角和俯角

如果您知道仰角或俯角，則可以使用直角三角形來找到距離。下圖顯示了這兩種型別的角度。

仰角是水平視線與指向目標的視線之間的夾角。例如，如果您站在地面上向上看山頂，您可以測量仰角。俯角是水平視線與向下指向目標的視線之間的夾角。例如，如果您站在山頂或建築物上，向下看某個物體，您可以測量俯角。您可以使用測角儀或經緯儀來測量這些角度。人們傾向於使用測角儀或經緯儀來測量樹木和其他高大物體的高度。在這裡，我們將解決幾個涉及這些角度和距離的問題。

示例 3

您站在一棵樹 20 英尺遠的地方，您測量到的仰角為 38°。這棵樹有多高？

解答:

解取決於您的身高，因為您是從視線水平測量仰角的。假設您身高 5 英尺。那麼下圖顯示了您正在解決的三角形。

該圖顯示，一旦我們找到 T 的值，我們必須將 5 英尺加到這個值才能找到三角形的總高度。為了找到 T，我們應該使用正切值

$\tan(38^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {T}{20}}$
$\tan(38^{\circ })=\,\!$	${\frac {T}{20}}$
$T=\,\!$	$20\tan(38^{\circ })\approx 15.63\,\!$
${\text{Height of tree}}\approx \,\!$	$20.63\ {\text{ft}}\,\!$

下一個例子展示了俯角。

例 4

你站在一棟大樓的頂端，看著遠處的一個公園。俯角是 53°。如果你所站的大樓高 100 英尺，公園離你有多遠？你的身高有影響嗎？

解答:

如果我們忽略人的身高，我們解決下面的三角形

給定俯角為 53°，上圖中角度 A 為 37°。我們可以使用正切函式來找到大樓到公園的距離

$\tan(37^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {d}{100}}$
$\tan(37^{\circ })=\,\!$	${\frac {d}{100}}$
$d=\,\!$	$100\tan(37^{\circ })\approx 75.36\ {\text{ft}}\,\!$

如果我們考慮人的身高，這會改變鄰邊的值。例如，如果這個人高 5 英尺，我們就有不同的三角形

$\tan(37^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {d}{105}}$
$\tan(37^{\circ })=\,\!$	${\frac {d}{105}}$
$d=\,\!$	$105\tan(37^{\circ })\approx 79.12\ {\text{ft}}\,\!$

如果你只是想估計一個距離，那麼你可以忽略測量者的身高。但是，在距離或長度較小的場合，測量者的身高會更加重要。例如，在樹高問題中，測量者的身高會比在建築物問題中對結果的影響更大，因為樹的高度更接近測量者，而不是建築物。

直角三角形和方位角

我們也可以使用直角三角形，透過給定的方位角來尋找距離。在航海中，方位角是兩個物體之間方向。在航空航海中，方位角是相對於正北方向，順時針旋轉的角度。下圖顯示了 70 度角

需要注意的是，導航問題中的角度測量方式與單位圓中的角度測量方式不同。此外，導航和測量中的角度也可能用北、東、南、西來表示。例如，N70° E 表示從北向東的角度，而 N70° W 表示從北向西的角度。N70° E 與上圖中的角度相同。N70° W 將導致第二象限中的角度。

以下示例展示瞭如何使用方位角查詢距離。

例 5

一艘船以 N50° E 的航線航行。該船航行直到它位於距離其出發港口正東 10 海里的港口正北方向。該船航行了多遠？

解答:

與 d 相對的角度是 50° 的餘角，即 40°。因此，我們可以使用餘弦函式找到 d

$\cos(40^{\circ })=\,\!$	${\frac {\text{adjacent}}{\text{hypotenuse}}}={\frac {10}{d}}$
$\cos(40^{\circ })=\,\!$	${\frac {10}{d}}$
$d\cos(40^{\circ })=\,\!$	$10\,\!$
$d=\,\!$	${\frac {10}{\cos(40^{\circ })}}\approx 13.05\ {\text{nm}}$

直角三角形的其他應用

一般來說，您可以使用三角學來解決任何涉及直角三角形的難題。接下來的幾個例子展示了可以使用直角三角形來查詢長度或距離的不同情況。

例 6

在第 3 課中，我們介紹了以下情況：您正在建造一個斜坡，以便輪椅使用者可以進入建築物。如果斜坡必須高 8 英尺，斜坡的角度必須約為 5°，那麼斜坡必須多長？

已知我們知道斜坡的角度和與角度相對邊的長度，我們可以使用正弦比來查詢斜坡的長度，即三角形的斜邊

$\sin(5^{\circ })=\,\!$	${\frac {8}{L}}$
$L\sin(5^{\circ })=\,\!$	$8\,\!$
$L=\,\!$	${\frac {8}{\sin(5^{\circ })}}\approx 91.8\ {\text{ft}}$

這看起來可能是一個很長的斜坡，但實際上，5° 的斜坡角度是美國殘疾人法案 (ADA) 要求的。這解釋了為什麼許多斜坡由幾個部分組成，或者有轉彎。需要額外的距離來彌補小的坡度。

直角三角形三角學也用於測量實際上無法測量的距離。下一個例子展示了月球和太陽之間距離的計算。此計算要求我們知道地球到月球的距離。在第 5 章中，您將學習正弦定理，這是計算地球到月球距離所必需的公式。在以下示例中，我們假設此距離，並使用直角三角形來查詢月球和太陽之間的距離。

例 7

地球、月球和太陽在月相為上弦月時形成一個直角三角形。地球到月球的距離約為 240,002.5 英里。太陽和月球之間的距離是多少？

解答:

令 d = 太陽和月球之間的距離。我們可以使用正切函式來求 d 的值

$\tan(89.85^{\circ })=\,\!$	${\frac {d}{240,002.5}}$
$d=\,\!$	$240,002.5\tan(89.85^{\circ })=91,673,992.71\ {\text{miles}}$

因此，太陽和月亮之間的距離遠大於地球和月亮之間的距離。

課程總結

在本課中，我們回到了直角三角形三角函式的主題，以解決涉及直角三角形的現實世界問題。為了找到長度或距離，我們使用了仰角、俯角、導航方位角以及其他產生直角三角形的實際情況。在後面的章節中，您將擴充套件本章的工作：您將學習使用三角函式比找到缺失的角度，並且您將學習如何確定非直角三角形的角度和邊。

思考點

在哪些情況下自然會出現直角三角形？
是否存在無法求解的直角三角形？

三角函式可以解決天文尺度上的問題，也可以解決地球上甚至分子或原子尺度上的問題。為什麼這是真的？

複習題

求解三角形
兩位朋友正在寫練習題來為三角函式考試做準備。薩姆為他的朋友安娜寫了以下問題來解決
在直角三角形ABC中，角C的度數為90度，邊c的長度為8英寸。求解該三角形。

安娜告訴薩姆這個三角形無法求解。薩姆說她錯了。誰是對的？解釋你的想法。
使用勾股定理來驗證例2中三角形的邊。
從地面到旗杆頂部的仰角測得為53°。如果測量距離為15英尺，那麼旗杆有多高？
從山頂到一座房子的俯角測得為14°。如果山高30英尺，那麼房子距離山頂多遠？
一架飛機從城市A起飛，以100°的方位角飛行。城市B位於城市A的正南方。當飛機位於城市B的東邊200英里時，飛機飛行了多遠？城市A和城市B相距多遠？
下圖所示的現代建築採用了一個外牆（左側所示），它與地板不呈90度角。右側的牆垂直於地板和天花板。

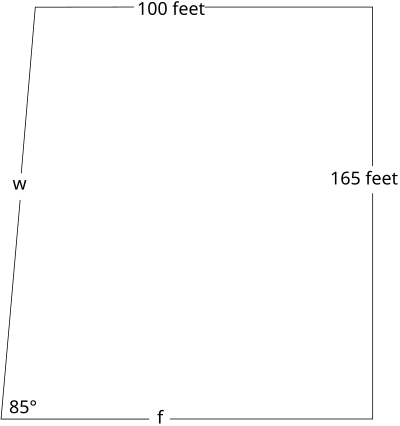
傾斜的外牆w的長度是多少？主地板f的長度是多少？
一位測量員正在測量一個池塘的寬度。她在池塘的另一邊選擇了一個地標，並測量了從距離原點50英尺的地方到這個地標的角度。池塘有多寬？
求邊x的長度