高中三角函式/任意角的三角函式

在上一課中，我們介紹了六個三角函式，並且以兩種方式處理這些函式：首先，在直角三角形中，其次，對於旋轉角度。在本課中，我們將擴充套件對單位圓中任意角度的三角函式的工作，包括負角度和大於 360 度的角度。在上一課中，我們處理了象限角和 30°、45° 和 60° 角。在本課中，我們將處理與這些角度相關的角度，以及單位圓中的其他角度。本課的一個關鍵思想是角度可以共享相同的三角值。這個想法將在整節課中進行闡述。

學習目標

識別單位圓中角度的參考角。
識別參考角為 30°、45° 和 60° 或象限角（包括負角度和度數大於 360° 的角度）的角度在單位圓上的有序對。
使用這些有序對確定這些角度的三角函式值。
使用表格和計算器查詢任意角度的三角函式值。

參考角和單位圓中的角度

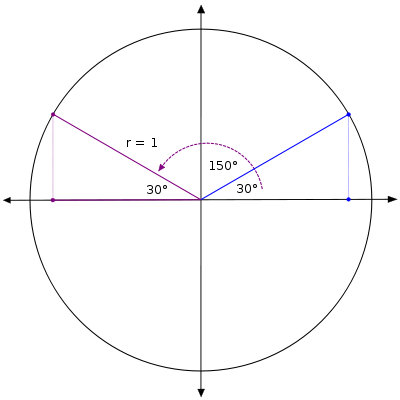
在上一課中，一個複習問題要求你考慮 150° 角。如果我們在標準位置繪製這個角，我們會看到這個角的終邊是 30° 的終邊關於y軸的對稱。

注意 150° 與負x軸形成一個 30° 角。因此，我們說 30° 是 150° 的參考角。正式地說，標準位置角度的參考角是與x軸最近部分形成的角度。請注意，30° 是許多角度的參考角。例如，它是 210° 和 −30° 的參考角。

一般來說，確定角度的參考角將有助於你確定角度的三角函式值。

示例 1

繪製每個角度並確定其參考角。

a. 140°

b. 240°

c. 380°

解決方案:

a. 140° 與x軸形成 40° 角。因此，參考角為 40°。

b. 240° 與x軸形成 60° 角。因此，參考角為 60°。

c. 380° 是 360° 的完整旋轉，加上另外 20°。所以這個角與 20° 同向，而 20° 是它的參考角。

如果一個角度的參考角為 30°、45° 或 60°，我們可以確定它在單位圓上的有序對，因此我們可以找到該角度的六個三角函式的值。例如，上面我們指出 150° 的參考角為 30°。由於它與 30° 的關係，150° 的有序對是 $\left(-{\tfrac {\sqrt {3}}{2}},{\tfrac {1}{2}}\right)$ 。現在我們可以找到 150° 的六個三角函式的值

$\cos(150^{\circ })=x={\frac {-{\sqrt {3}}}{2}}$	$\sec(150^{\circ })={\frac {1}{x}}={\frac {1}{\frac {-{\sqrt {3}}}{2}}}={\frac {-2}{\sqrt {3}}}$
$\sin(150^{\circ })=y={\frac {1}{2}}$	$\csc(150^{\circ })={\frac {1}{y}}={\frac {1}{\frac {1}{2}}}=2$
$\tan(150^{\circ })={\frac {y}{x}}={\frac {\frac {1}{2}}{\frac {-{\sqrt {3}}}{2}}}={\frac {1}{-{\sqrt {3}}}}$	$\cot(150^{\circ })={\frac {x}{y}}={\frac {\frac {-{\sqrt {3}}}{2}}{\frac {1}{2}}}=-{\sqrt {3}}$

示例 2

找到 240° 的有序對，並用它來找到 sin 240° 的值。

解決方案:

sin(240°) = ${\tfrac {-{\sqrt {3}}}{2}}$

正如我們在示例 1 中發現的，240° 的參考角是 60°。下圖顯示了 60° 以及單位圓中其他三個以 60° 為參考角的角。

240° 的終邊是 60° 的終邊關於兩個軸的反射。所以該點的座標是 $\left(-{\tfrac {1}{2}},-{\tfrac {\sqrt {3}}{2}}\right)$ 。y 座標是正弦值，所以 sin(240°) = ${\tfrac {-{\sqrt {3}}}{2}}$ 。

就像上圖顯示了 60° 和三個相關的角一樣，我們也可以為 30° 和 45° 製作類似的圖形。

示例 3

求 cot(300°) 的值。

解決方案:

cot(300°) = $-{\tfrac {1}{\sqrt {3}}}$

使用上面的圖形，你會發現該點的座標是 $\left({\tfrac {1}{2}},-{\tfrac {\sqrt {3}}{2}}\right)$ 。因此餘切值為

$\cot(300^{\circ })={\frac {x}{y}}={\frac {\frac {1}{2}}{-{\frac {\sqrt {3}}{2}}}}={\frac {1}{2}}\cdot -{\frac {2}{\sqrt {3}}}=-{\frac {1}{\sqrt {3}}}$

我們還可以使用參考角的概念和我們已經確定的座標對來確定其他角的三角函式的值。

負角的三角函式

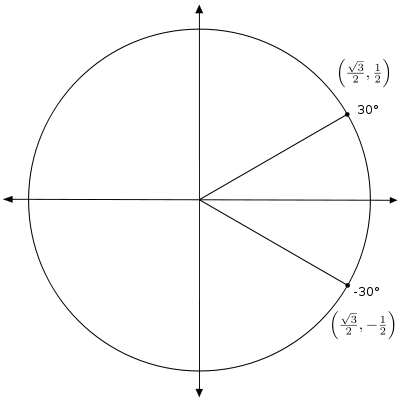
回想一下，繪製負角意味著順時針旋轉。下圖顯示了 -30°。

注意，這個角與 330° 是終邊相同的。因此該點的座標是 $\left({\tfrac {\sqrt {3}}{2}},-{\tfrac {1}{2}}\right)$ 。我們可以使用這個座標對來求出 -30° 的任何三角函式的值。例如，cos(-30°) = x = ${\tfrac {\sqrt {3}}{2}}$ 。

一般來說，如果一個負角的參考角是 30°、45° 或 60°，或者它是一個象限角，我們可以找到它的座標對，因此我們可以確定該角的任何三角函式的值。

示例 4

求每個表示式的值。

a. sin(-45°)

b. sec(-300°)

c. cos(-90°)

解決方案:

a. sin(-45°) = $-{\tfrac {\sqrt {2}}{2}}$

−45° 位於第四象限，其參考角為 45°。也就是說，該角度與 315° 終邊重合。因此，有序對是 $\left({\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}}\right)$ ，正弦值為 $-{\tfrac {\sqrt {2}}{2}}$ 。

b. sec(-300°) = 2

角度 −300° 位於第一象限，其參考角為 60°。也就是說，該角度與 60° 終邊重合。因此，有序對是 $\left({\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ ，正割值為 ${\tfrac {1}{x}}={\tfrac {1}{\frac {1}{2}}}=$ 2。

c. cos(−90°) = 0

角度 −90° 與 270° 終邊重合。因此，有序對為 (0, −1)，餘弦值為 0。

我們還可以利用對參考角和有序對的瞭解，找到大於 360 度的角度的三角函式值。

大於 360 度的角度的三角函式

考慮角度 390°。正如你之前所學，你可以將這個角度視為一個完整的 360 度旋轉，再加上額外的 30 度。因此，390° 與 30° 終邊重合。正如你在上面關於負角度的討論中看到的那樣，這意味著 390° 與 30° 具有相同的有序對，因此它們具有相同的三角函式值。例如，cos(390°) = cos(30°) = ${\tfrac {\sqrt {3}}{2}}K$

一般來說，如果一個大於 360 度的角度的參考角為 30°、45° 或 60°，或者它是一個象限角，我們可以找到它的有序對，因此我們可以找到該角度的任何三角函式的值。第一步是確定參考角。

例 5

求每個表示式的值。

a. sin(420°)

b. tan(840°)

c. cos(540°)

解決方案:

a. sin(420°) = ${\tfrac {\sqrt {3}}{2}}$

420° 是一個完整的 360 度旋轉，再加上額外的 60 度。因此，該角度與 60° 終邊重合，因此它具有相同的有序對， $\left({\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ 。正弦值是 *y* 座標。

b. tan(840°) = −√3

840° 是兩個完整的旋轉，或 720 度，再加上額外的 120 度

840 = 360 + 360 + 120

因此，840° 與 120° 終邊重合，所以有序對是 $\left(-{\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ 。正切值可以透過以下方法找到

\tan(840^{\circ })=\tan(120^{\circ })={\frac {y}{x}}={\frac {\frac {\sqrt {3}}{2}}{-{\frac {1}{2}}}}={\frac {\sqrt {3}}{2}}\cdot -{\frac {2}{1}}=-{\sqrt {3}}

c. cos(540°) = −1

540° 是一個完整的 360 度旋轉，再加上額外的 180 度。因此，該角度與 180◦ 終邊重合，有序對為 (−1, 0)。所以餘弦值為 −1。

到目前為止，我們處理的所有角度都是 30、45、60 和 90 的倍數。接下來，我們將找到其他角度的三角函式的近似值。

三角函式值表

在學習這章的過程中，你將學習到三角函式的不同應用。在許多情況下，你將需要找到一個角度的函式值，該角度不一定是我們迄今為止處理過的“特殊”角度之一。傳統上，教科書會為學生提供包含三角函式值的表格。下面是一個表格，它提供了幾個角度的正弦、餘弦和正切值的近似值。

表 1.11
角度 (°)	餘弦	正弦	正切
0	1.000	0.000	0.000
5	0.9962	0.0872	0.0875
10	0.9848	0.1736	0.1763
15	0.9659	0.2588	0.2679
20	0.9397	0.3420	0.3640
25	0.9063	0.4226	0.4663
30	0.8660	0.5000	0.5774
35	0.8192	0.5736	0.7002
40	0.7660	0.6428	0.8391
45	0.7071	0.7071	1.0000
50	0.6428	0.7660	1.1918
55	0.5736	0.8192	1.4281
60	0.5000	0.8660	1.7321
65	0.4226	0.9063	2.1445
70	0.3420	0.9397	2.7475
75	0.2588	0.9659	3.7321
80	0.1736	0.9848	5.6713
85	0.0872	0.9962	11.4301
90	0.0000	1.0000	未定義
95	−0.0872	0.9962	−11.4301
100	−0.1736	0.9848	−5.6713
105	−0.2588	0.9659	−3.7321
110	−0.3420	0.9397	−2.7475
115	−0.4226	0.9063	−2.1445
120	−0.5000	0.8660	−1.7321
125	−0.5736	0.8192	−1.4281
130	−0.6428	0.7660	−1.1918
135	−0.7071	0.7071	−1.0000
140	−0.7660	0.6428	−0.8391
145	−0.8192	0.5736	−0.7002
150	−0.8660	0.5000	−0.5774
155	−0.9063	0.4226	−0.4663
160	−0.9397	0.3420	−0.3640
165	−0.9659	0.2588	−0.2679
170	−0.9848	0.1736	−0.1763
175	−0.9962	0.0872	−0.0875
180	−1.0000	0.0000	0.0000

我們可以用表格來識別近似值。

例 6

使用上面的表格，找到每個表示式的近似值。

a. sin(130°)

b. cos(15°)

c. tan(50°)

解決方案:

a. sin(130°) ≈ 0.7660

我們可以透過查詢表格中 130 度的行來確定正弦值。正弦值位於表格的第三行。請注意，這是一個近似值。我們可以透過考慮一個接近 130 度的角，120 度，來評估此值的合理性。我們知道 120 度的有序對是 $\left(-{\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ ，因此正弦值為 ${\tfrac {\sqrt {3}}{2}}$ ≈ 0.8660，這也位於表格中。由於這些角的終邊與單位圓的交點，sin(130°) ≈ 0.7660 是合理的，它略小於 120 度的正弦值。

b. cos(15°) ≈ 0.9659

我們可以透過查詢 15 度的行來確定此餘弦值。餘弦值位於第二列。同樣，我們可以透過考慮一個附近的角來確定此值是否合理。15° 在 0° 和 30° 之間，其餘弦值在這兩個角的餘弦值之間。

c. tan(50°) ≈ 1.1918

我們可以透過查詢 50 度的行，並讀取表格的最後一列來確定此正切值。在複習題中，您將被要求解釋為什麼正切值似乎是合理的。

使用計算器查詢值

如果您有科學計算器，您可以確定任何角的任何三角函式的值。在這裡，我們將重點介紹使用 TI 圖形計算器查詢值。

首先，您的計算器需要處於正確的“模式”。在第 2 章中，您將學習另一種測量角度的系統，稱為弧度制。在本章中，我們以度為單位測量角度。（這類似於以英里或公里為單位測量距離。它只是不同的測量系統。）我們需要確保計算器以度為單位工作。為此，請按[MODE]. 您將看到第三行顯示 Radian Degree。如果 Degree 被突出顯示，則您處於正確的模式。如果 Radian 被突出顯示，請向下滾動到此行，向右滾動到 Degree，然後按[ENTER]. 這將突出顯示 Degree。然後按 2^nd[MODE]返回主螢幕。

現在您可以計算任何值。例如，我們可以驗證上述表格中的值。要查詢 sin(130°)，請按[SIN] [1] [3] [0] [ENTER]. 計算器應返回值 .7660444431。

您可能已經注意到，計算器在 SIN 後提供了 "("。在前面的計算中，您實際上可以省略 ")"。但是，在更復雜的計算中，省略右括號")" 會導致問題。養成習慣，始終閉合括號是個好主意。

您也可以使用計算器查詢更復雜表示式的值。

例 7

使用計算器查詢 sin(25°) + cos(25°) 的近似值。將您的答案四捨五入到小數點後 4 位。

解決方案:

sin(25°) + cos(25°) ≈ 1.3289

要使用 TI 圖形計算器，請按[SIN] [25] [+] [COS] [2] [5] [ENTER]. 計算器應返回數字 1.328926049。四捨五入到 1.3289。

課程總結

在本課中，我們已經研究了我們可以為任何角度找到六個三角函式的精確值或近似值的概念。我們首先定義了參考角的概念，這對於找到單位圓中某些角度的有序對很有用。我們已經找到了“特殊”角度的三角函式的精確值，包括負角以及度數大於 360 度的角。我們還使用表格和計算器找到了其他角度值的近似值。在接下來的課程中，我們將使用本課中的概念來 (1) 檢查三角函式之間的關係，以及 (2) 將三角函式應用於實際情況。

值得思考的問題

角度的度數與其參考角之間有什麼區別？在哪些情況下這些度數相同？
哪些角具有相同的餘弦值或相同的正弦值？哪些角具有相反的餘弦值和正弦值？

複習題

說明每個角的參考角。
(a) 190°

(b) −60°

(c) 1470°

(d) −135°
說明每個角的有序對。
(a) 300°

(b) −150°

(c) 405°
求每個表示式的值。
(a) sin(210°)

(b) tan(270°)

(c) csc(120°)
求每個表示式的值。
(a) sin(510°)

(b) cos(930°)

(c) csc(405°)
求每個表示式的值。
(a) cos(−150°)

(b) tan(−45°)

(c) sin(−240°)
使用本課中的表格查詢 cos(100°) 的近似值。
使用本課中的表格來近似一個正弦值為 0.2 的角度的度數。
在例 6c 中，我們發現 tan(50°) ≈ 1.1918。使用您對特殊角的瞭解來解釋為什麼此值是合理的。
使用計算器查詢每個值。四捨五入到小數點後 4 位。
(a) sin(118°)

(b) tan(55°)
使用下面的表格或計算器來探索三角函式之間的和與積關係。
考慮以下函式
f(x) = sin(x+x) 和 g(x) = sin(x) + sin(x)

h(x) = sin(x) · sin(x) 和 j(x) = sin(x²)

您是否在這些函式中觀察到任何規律？函式之間是否存在任何等式？您能對所有 a、b 值的 sin(a) + sin(b) 和 sin(a+b) 作出一般性推測嗎？

sin(a) · sin(a) 和 sin(a²) 又如何呢？

a° b° sin a + sin b sin(a+b)
10 30 0.6736 0.6428
20 60 1.2080 0.9848
55 78 1.7973 0.7314
122 25 1.2707 0.5446
200 75 0.6239 −0.9962
使用計算器或您對特殊角的瞭解來填寫表格中的值，然後使用這些值來推測 (sin a)² 和 (cos a)² 之間的關係。如果您使用計算器，請將所有值四捨五入到小數點後 4 位。
a (sin a)² (cos a)²
0
25
45
80
90
120
250

複習答案

(a) 10°

(b) 60°

(c) 30°

(d) 45°
(a) $\left({\tfrac {1}{2}},-{\tfrac {\sqrt {3}}{2}}\right)$

(b) $\left(-{\tfrac {\sqrt {3}}{2}},-{\tfrac {1}{2}}\right)$

(c) $\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}}\right)$
(a) $-{\tfrac {1}{2}}$

(b) 未定義

(c) ${\tfrac {2}{\sqrt {3}}}$
(a) ${\tfrac {1}{2}}$

(b) $-{\tfrac {\sqrt {3}}{2}}$

(c) √2
(a) $-{\tfrac {\sqrt {3}}{2}}$

(b) −1

(c) ${\tfrac {\sqrt {3}}{2}}$
−0.1736
介於 165 度和 160 度之間。
這是合理的，因為 tan(45°) = 1 。
(a) 0.8828

(b) 1.4281
猜想：sin a + sin b ≠ sin(a+b) 。
猜想：(sin a)² + (cos a)² = 1 。
a (sin a)² (cos a)²
0 0 1
25 0.1786 0.8216
45 0.5000 0.5000
80 0.9698 0.0302
90 1 0
120 0.7500 0.2500
250 0.8830 0.1170