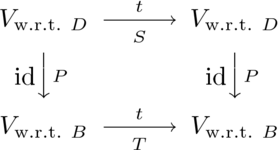- 問題 1
對於

檢查 .
.
- 解答
一種解決方法是從左到右。

- 建議所有讀者完成此練習。
- 問題 3
證明這些矩陣不相似。

- 解答
高斯消元法表明,第一個矩陣代表秩為二的對映,而第二個矩陣代表秩為三的對映。
- 問題 4
考慮變換  ,其描述為
,其描述為  、
、 和
和  。
。
- 求
 ,其中
,其中  。
。 - 求
 ,其中
,其中  。
。 - 求矩陣
 ,使得
,使得  。
。
- 解答
- 因為
 用
用  的成員來描述,所以求矩陣表示很容易。
的成員來描述,所以求矩陣表示很容易。
給出如下結果。
- 我們將找到
 ,
, 和
和  ,以找到它們分別如何相對於
,以找到它們分別如何相對於  表示。我們知道
表示。我們知道  ,另外兩個很容易看出來:
,另外兩個很容易看出來: 和
和  。我們可以直接得到每個向量的表示
。我們可以直接得到每個向量的表示
因此,對映的表示為。
- 該圖適用於此
 和
和  ,
,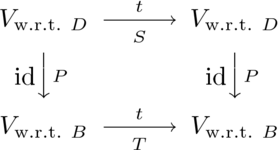
表明  .
.
- 建議所有讀者完成此練習。
- 問題 5
用這種方式展示一個非平凡的相似關係:令  作用於
作用於

並選擇兩個基,並表示  關於它們
關於它們  和
和  。然後計算
。然後計算  和
和  來改變從
來改變從  到
到  的基以及返回。
的基以及返回。
- 解答
基的一個可能的選擇是

(這個  是對映描述所建議的)。為了找到矩陣
是對映描述所建議的)。為了找到矩陣  ,求解關係
,求解關係

得到  ,
,  ,
,  以及
以及  .
.

尋找  涉及更多計算。我們首先找到
涉及更多計算。我們首先找到  。關係
。關係

給出  以及
以及  ,所以
,所以

使得

因此  對第一個基向量
對第一個基向量  的作用方式如下。
的作用方式如下。

對  的計算類似。關係
的計算類似。關係

得出  和
和  ,因此
,因此

使得

因此  作用於第二個基向量
作用於第二個基向量  的方式如下。
的方式如下。

因此

以及這些是基變更矩陣。

對這些計算進行檢查是例行的。

- 問題 6
用對映解釋 示例 1.3。
- 解答
零對映的唯一表示是零矩陣,無論基底對  是什麼,特別地,對於任何單個基底
是什麼,特別地,對於任何單個基底  ,我們有
,我們有  。恆等對映的情況是相關的,但略有不同:恆等對映的唯一表示,相對於任何
。恆等對映的情況是相關的,但略有不同:恆等對映的唯一表示,相對於任何  ,是恆等矩陣
,是恆等矩陣  。(注:當然,我們已經看到一些例子,其中
。(注:當然,我們已經看到一些例子,其中  並且
並且  ——事實上,我們已經看到,任何非奇異矩陣都是恆等對映相對於某個
——事實上,我們已經看到,任何非奇異矩陣都是恆等對映相對於某個  的表示。)
的表示。)
- 建議所有讀者完成此練習。
- 建議所有讀者完成此練習。
- 問題 8
證明如果兩個矩陣相似,並且其中一個是可逆的,則另一個也是可逆的。
- 解答
矩陣相似是矩陣等價的一個特例(如果矩陣相似,則它們是矩陣等價的),而矩陣等價保持非奇異性。(這是相似矩陣具有相同行列式的規則的擴充套件,可以用來作為可逆性的指標。)
- 建議所有讀者完成此練習。
- 問題 10
考慮一個矩陣,它表示關於某個  ,在
,在  中關於
中關於  軸的反射。 也考慮一個矩陣,它表示關於某個
軸的反射。 也考慮一個矩陣,它表示關於某個  ,關於
,關於  軸的反射。 它們必須相似嗎?
軸的反射。 它們必須相似嗎?
- 解答
令  和
和  為反射對映(有時稱為“翻轉”)。 對於任何基底
為反射對映(有時稱為“翻轉”)。 對於任何基底  和
和  ,矩陣
,矩陣  和
和  是相似的。 首先注意到
是相似的。 首先注意到

是相似的,因為第二個矩陣是關於基底  表示的
表示的  。
。

其中  .
.
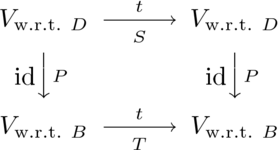
現在,結論來自於問題 9的傳遞性部分。
為了不依賴於該練習,寫下 


因此矩陣  和
和  是相似的。
是相似的。
- 問題 11
證明相似性保持行列式和秩。反之是否成立?
- 解答
我們必須證明,如果兩個矩陣相似,那麼它們具有相同的行列式和相同的秩。行列式和秩都是矩陣的性質,我們已經證明它們在矩陣等價下保持不變。因此,它們在相似性(它是矩陣等價的一個特例:如果兩個矩陣相似,那麼它們是矩陣等價的)下保持不變。
為了證明該陳述而不引用關於矩陣等價的結果,首先要注意秩是對映的性質(它是值域的維數),並且由於我們已經證明對映的秩是表示的秩,因此它對於所有表示都必須相同。至於行列式, .
.
該陳述的反之不成立;例如,存在行列式相同的矩陣,但它們並不相似。為了驗證這一點,考慮一個行列式為零的非零矩陣。它與零矩陣不相似,零矩陣僅與其自身相似,但它們具有相同的行列式。秩的論證大體相同。
- 建議所有讀者完成此練習。
- 建議所有讀者完成此練習。
- 問題 17
相似性是否保持求和?
- 解答
否。這裡有一個例子,其中有兩對,每對都是兩個相似的矩陣

和

(這個例子大部分是任意的,但並非完全如此,因為兩個左側的中心矩陣加起來等於零矩陣)。需要注意的是,這些相似矩陣的和並不相似。

因為零矩陣只與自身相似。
- Halmos, Paul P. (1958), Finite Dimensional Vector Spaces (第二版), Van Nostrand.