線性代數/命題

論證中的爭議點是命題。數學家通常會在證明之前寫出完整的論點，並將其標記為定理（對於主要論點）、推論（對於緊接在先前論點之後的論點）或引理（對於主要用於證明其他結果的結果）。

表達命題的陳述可能很複雜，包含許多子部分。整個命題的真假既取決於各部分的真值，也取決於用來將各部分組合成陳述的詞語。

非

例如，當 $P$ 是一個命題時，"並非 $P$" 是真的，前提是 $P$ 是假的。因此，"$n$ 不是素數" 只有在 $n$ 是較小整數的乘積時才為真。

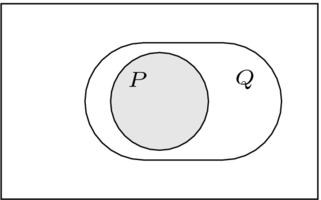
我們可以用文氏圖來描述"非"操作。

框包含所有自然數，圓圈內是素數，陰影區域包含滿足"非 $P$" 的數字。

要證明"非 $P$" 語句成立，請證明 $P$ 是假的。

與

考慮語句形式"$P$ 與 $Q$"。為了使該語句為真，兩半都必須成立：" $7$ 是素數，$3$ 也是" 是真的，而 "$7$ 是素數，$3$ 不是" 是假的。

這是"$P$ 與 $Q$" 的文氏圖。

要證明"$P$ 與 $Q$"，請證明每一半都成立。

或

當其中一個部分成立時，"$P$ 或 $Q$" 為真："$7$ 是素數，或 $4$ 是素數" 為真，而 "$7$ 不是素數，或 $4$ 是素數" 為假。我們對“或”採取包含性，因此，如果兩個部分都為真，"$7$ 是素數，或 $4$ 不是"，那麼整個語句就為真。（在日常語言中，有時“或”的意思是排他的——“吃蔬菜或沒有甜點”並不意味著兩個部分都成立——但我們不會用“或”來表達這種意思。）

“或”的維恩圖包含兩個圓的所有部分。

為了證明"$P$ 或 $Q$"，請證明在所有情況下，至少有一個部分成立（有時可能是其中一個部分，有時是另一個部分，但始終至少有一個成立）。

如果-那麼

“如果 $P$ 那麼 $Q$” 語句（有時寫成“$P$ 蘊含 $Q$” 或簡稱為“$P$ 蘊含 $Q$” 或“$P\implies Q$”) 除非 $P$ 為真而 $Q$ 為假，為真。因此“如果 $7$ 是素數，那麼 $4$ 不是”為真，而“如果 $7$ 是素數，那麼 $4$ 也是素數”為假。（與日常用語中“如果 $P$ 那麼 $Q$” 的含義不同，在數學中“如果 $P$ 那麼 $Q$” 不意味著 $P$ 發生在 $Q$ 之前或導致 $Q$。）

更微妙的是，在數學中，“如果 $P$ 那麼 $Q$” 當 $P$ 為假時成立：“如果 $4$ 是素數，那麼 $7$ 是素數” 和 “如果 $4$ 是素數，那麼 $7$ 不是” 都是真命題，有時被稱為 **空真**。我們採用這種約定，因為我們希望像“如果一個數是完全平方，那麼它就不是素數” 這樣的命題為真，例如，當這個數為 $5$ 或當這個數為 $6$ 時。

這個圖表

表明 $Q$ 只要 $P$ 成立就成立（另一種說法是“$P$ 足以得到 $Q$”)。再次注意，如果 $P$ 不成立，$Q$ 可能成立也可能不成立。

建立蘊涵關係主要有兩種方式。第一種是直接方式：假設 $P$ 為真，並利用該假設證明 $Q$ 為真。例如，為了證明“如果一個數能被 5 整除，那麼該數的兩倍就能被 10 整除”，我們假設該數為 $5n$，並推匯出 $2(5n)=10n$。 第二種是間接方式：證明逆否命題：“如果 $Q$ 為假，那麼 $P$ 也為假”（換句話說，“$Q$ 只有在 $P$ 也為假時才可能為假”。例如，為了證明“如果一個數是素數，那麼它就不是一個完全平方數”，我們論證如果它是一個平方數 $p=n^{2}$，那麼它就可以分解成 $p=n\cdot n$，其中 $n<p$，因此就不是素數（當然 $p=0$ 或 $p=1$ 無法得到 $n<p$，但根據定義它們是非素數)。

請注意這種命題形式的兩個特點。

首先，一個“如果 $P$ 那麼 $Q$” 的結果有時可以透過削弱 $P$ 或加強 $Q$ 來改進。因此，“如果一個數字可以被 $p^{2}$ 整除，那麼它的平方也可以被 $p^{2}$ 整除” 可以透過放寬它的假設來升級：“如果一個數字可以被 $p$ 整除，那麼它的平方可以被 $p^{2}$ 整除”，或者透過收緊它的結論來升級：“如果一個數字可以被 $p^{2}$ 整除，那麼它的平方可以被 $p^{4}$ 整除”。

其次，在證明了“如果 $P$ 那麼 $Q$” 之後，下一步是研究是否存在 $Q$ 成立但 $P$ 不成立的情況。目的是更好地理解 $P$ 和 $Q$ 之間的關係，以便加強命題。

等價

當 $P$ 蘊含 $Q$，以及 $Q$ 蘊含 $P$ 時，條件語句無法得到改進。 有些表達方式包括：“$P$ 當且僅當 $Q$”， “$P$ 當且僅當 $Q$”, “$P$ 和 $Q$ 在邏輯上是等價的”， “$P$ 是得到 $Q$ 的必要和充分條件”， “$P\iff Q$”。 例如，“一個數能被一個素數整除，當且僅當該數的平方能被該素數的平方整除”。

此圖表明 $P$ 和 $Q$ 在完全相同的情況下成立。

雖然在簡單的論證中，像 “$P$ 當且僅當 $R$，該條件成立，當且僅當 $S$ ...” 這樣的鏈條可能很實用，但通常我們透過分別證明“如果 $P$ 則 $Q$” 和 “如果 $Q$ 則 $P$” 來證明等價性。