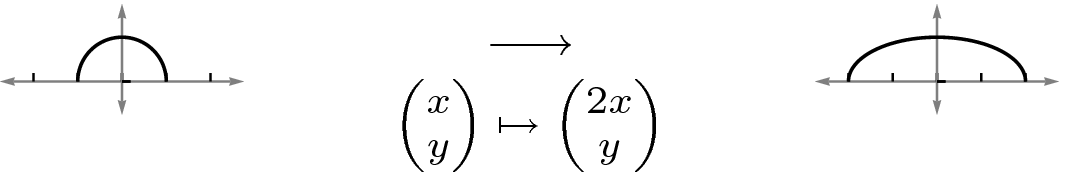線性代數/主題：特徵值的幾何意義

--參考線性變換幾何意義主題---

從基本運算的角度來刻畫線性變換在某些方面是不錯的（例如，我們可以很容易地看出直線被對映到直線，因為投影、擴張、反射和錯切等運算都會將直線對映到直線），但是當一個對映被表示為許多小的運算的複合時——無論這些運算多麼簡單——其描述都不夠理想。我們最後以另一種方式，一種更整體的方式，來描繪$\mathbb {R} ^{2}$變換的幾何效應。

該領域中的圖片僅僅給出了對映對定義域中一個或兩個元素的作用。儘管我們知道一個變換完全由它對基的元素的作用來描述，因此嚴格來說，描述$\mathbb {R} ^{2}$的變換隻需要描述它將任何基的兩個向量對映到哪裡，但這些圖片似乎並沒有傳達多少幾何直覺。我們能否透過新增更多資訊來闡明線性對映的幾何意義，但又不至於新增太多資訊導致圖片變得混亂？

一個$\mathbb {R} ^{2}$的變換將過原點的直線對映到過原點的直線。因此，一條直線$y=k_{1}x$上的兩點都會被對映到另一條直線上，比如說$y=k_{2}x$。考慮這兩點。其中一點是另一點的倍數，因此我們可以用第二點表示為第一點的$r$倍，其中$r$是某個標量。

${\begin{pmatrix}x\\k_{1}x\end{pmatrix}}\quad {\mbox{and}}\quad {\begin{pmatrix}(rx)\\k_{1}(rx)\end{pmatrix}}$

比較它們的像。

${\begin{pmatrix}a&c\\b&d\end{pmatrix}}{\begin{pmatrix}x\\k_{1}x\end{pmatrix}}={\begin{pmatrix}ax+ck_{1}x\\bx+dk_{1}x\end{pmatrix}}\qquad {\begin{pmatrix}a&c\\b&d\end{pmatrix}}{\begin{pmatrix}(rx)\\k_{1}(rx)\end{pmatrix}}={\begin{pmatrix}a(rx)+ck_{1}(rx)\\b(rx)+dk_{1}(rx)\end{pmatrix}}$

第二個向量是第一個向量的$r$倍，第二個向量的像是第一個向量的$r$倍。變換不僅保持了向量共線的性質，還保持了向量的相對比例。也就是說，變換對過原點的直線上的點具有統一的作用。為了描述對映對整條直線的影響，我們只需要描述它對該直線上任意一個非零點的影響。

由於空間中的每個點都位於過原點的某條直線上，為了理解$\mathbb {R} ^{2}$的線性變換的作用，只需從每條過原點的直線上選擇一個點（例如單位圓上半部分的點），並展示對映對這組點的作用。

下面是對於一個簡單的擴張的這種圖片。

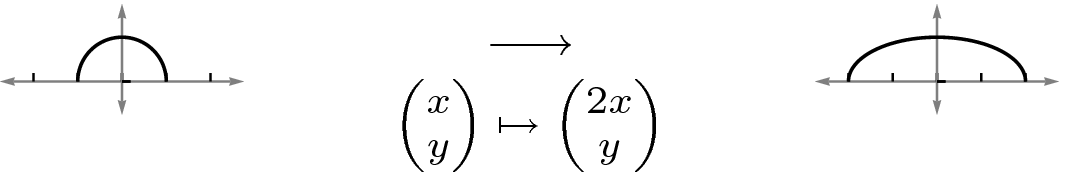
下面，同一個對映用圓及其像疊加在一起顯示。

當然，這裡的幾何關係更加明顯。例如，我們可以看到一些過原點的直線實際上被對映到自身：$x$軸被對映到$x$軸，$y$軸被對映到$y$軸。

這是之前顯示的翻轉，這裡疊加了圓及其影像。

這是之前顯示的錯切。

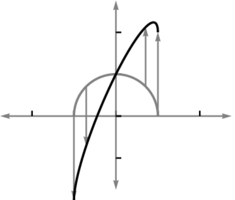
將此對映對單位正方形的影響的影像與這幅影像進行對比。

這是一個稍微複雜一些的對映（第二個座標函式與前一幅圖中的對映相同，但第一個座標函式不同）。

觀察到一些向量正在被同時拉伸和旋轉某個角度。

${\begin{pmatrix}x\\2x\end{pmatrix}}\mapsto {\begin{pmatrix}x\\k_{1}x\end{pmatrix}}$

而其他的只是被拉伸，根本沒有旋轉。

${\begin{pmatrix}x\\3x\end{pmatrix}}\mapsto {\begin{pmatrix}x\\3x\end{pmatrix}}$

練習

問題 1

顯示每個矩陣對單位圓上半部分的影響。

1. ${\begin{pmatrix}1&1\\2&2\end{pmatrix}}$
2. ${\begin{pmatrix}2&3\\1&1\end{pmatrix}}$
3. ${\begin{pmatrix}2&3\\1&-1\end{pmatrix}}$

哪些向量保持在過原點的同一條直線上？

解答