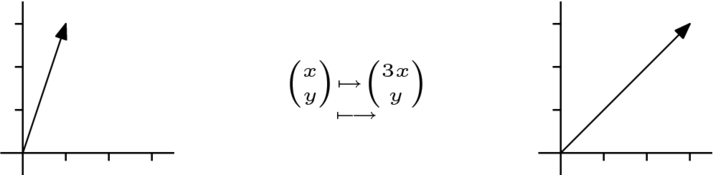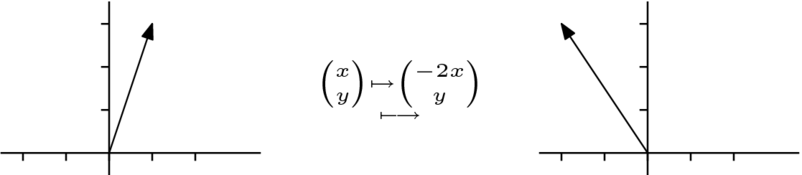下面的圖片對比了 和
和  ,它們是非線性的,與
,它們是非線性的,與  和
和  ,它們是線性的。所有四張圖片都顯示了左側的定義域
,它們是線性的。所有四張圖片都顯示了左側的定義域  對映到右側的陪域
對映到右側的陪域  。箭頭追蹤每個對映傳送
。箭頭追蹤每個對映傳送  、
、 、
、 、
、 和
和  的位置。注意非線性對映在將定義域轉換為值域時如何扭曲定義域。例如,
的位置。注意非線性對映在將定義域轉換為值域時如何扭曲定義域。例如, 比
比  更遠離
更遠離  ——對映不均勻地擴充套件了定義域,使得靠近
——對映不均勻地擴充套件了定義域,使得靠近  的區間在傳遞到值域時比靠近
的區間在傳遞到值域時比靠近  的區間擴充套件得更遠。
的區間擴充套件得更遠。
線性對映更友好,更規則,因為對於每個對映,整個定義域都以相同的因子擴充套件。
從  到
到  的唯一線性對映是乘以一個標量。在更高維度下,可能會發生更多的情況。 例如,這個
的唯一線性對映是乘以一個標量。在更高維度下,可能會發生更多的情況。 例如,這個  的線性變換,將向量逆時針旋轉,不僅僅是標量乘法。
的線性變換,將向量逆時針旋轉,不僅僅是標量乘法。
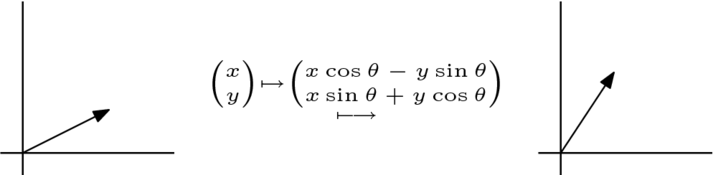
將  中的向量投影到
中的向量投影到  平面上的變換也不是簡單的縮放。
平面上的變換也不是簡單的縮放。

儘管如此,即使在更高維度下,情況也不會太複雜。
下面,我們使用標準基來表示每個線性對映  為一個矩陣
為一個矩陣  。回想一下,任何
。回想一下,任何  可以分解為
可以分解為  ,其中
,其中  和
和  是非奇異的,而
是非奇異的,而  是一個部分單位矩陣。 此外,回想一下,非奇異矩陣可以分解為初等矩陣
是一個部分單位矩陣。 此外,回想一下,非奇異矩陣可以分解為初等矩陣  ,這些矩陣是從單位矩陣
,這些矩陣是從單位矩陣  透過一個高斯步驟獲得的
透過一個高斯步驟獲得的
![{\displaystyle I{\xrightarrow[{}]{k\rho _{i}}}M_{i}(k)\qquad I{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}P_{i,j}\qquad I{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}C_{i,j}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8efb67d5d26695581b1ba19fa3f9d1f49e49f4ed)
( ,
,  ). 因此,如果我們理解由部分單位矩陣描述的線性對映的影響,以及由基本矩陣描述的線性對映的影響,那麼在某種程度上,我們將理解任何線性對映的影響。(下面的圖片只關注
). 因此,如果我們理解由部分單位矩陣描述的線性對映的影響,以及由基本矩陣描述的線性對映的影響,那麼在某種程度上,我們將理解任何線性對映的影響。(下面的圖片只關注 的變換,以方便繪製,但這些陳述適用於從任何
的變換,以方便繪製,但這些陳述適用於從任何 到任何
到任何 的對映。)
的對映。)
由部分單位矩陣表示的線性變換的幾何效果是投影。

對於 矩陣,由該矩陣表示的變換的幾何作用(相對於標準基)是沿
矩陣,由該矩陣表示的變換的幾何作用(相對於標準基)是沿 軸將向量拉伸
軸將向量拉伸 倍。該對映沿
倍。該對映沿 軸拉伸了
軸拉伸了 倍。
倍。
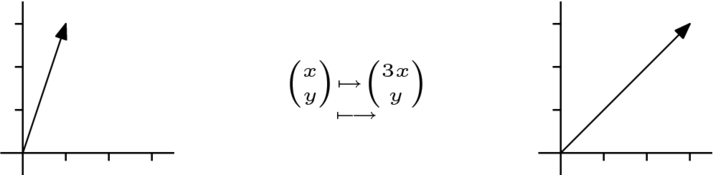
注意,如果 或者如果
或者如果 ,那麼
,那麼 分量朝另一個方向移動;在這裡,朝左側移動。
分量朝另一個方向移動;在這裡,朝左側移動。
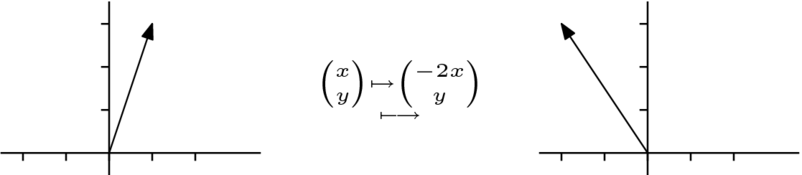
這兩個都是伸縮變換。
由 置換矩陣表示的變換的作用是交換
置換矩陣表示的變換的作用是交換 軸和
軸和 軸;這是一種特殊的反射。
軸;這是一種特殊的反射。

在更高維度中,涉及多個軸的置換可以分解為一對軸交換的組合 - 請參見問題 5。
剩下的情況是形式為  的矩陣。回想一下,例如
的矩陣。回想一下,例如  執行
執行  。
。

在下圖中,第一個分量為  的向量
的向量  比第一個分量為
比第一個分量為  的向量
的向量  受到的影響更小——
受到的影響更小——  只比
只比  高
高  ,而
,而  比
比  高
高  。
。

任何第一個分量為  的向量都會受到影響,就像
的向量都會受到影響,就像  一樣;它會向上滑動
一樣;它會向上滑動  。任何第一個分量為
。任何第一個分量為  的向量會向上滑動
的向量會向上滑動  ,就像
,就像  一樣。也就是說,由
一樣。也就是說,由  表示的變換會影響向量,具體取決於它們的
表示的變換會影響向量,具體取決於它們的  個分量。
個分量。
從另一個角度看,可以考慮此對映對單位正方形的作用。在下圖中,第一個分量為  的向量,例如原點,在垂直方向上沒有移動,但第一個分量為正值的向量會向上移動。在這裡,所有第一個分量為
的向量,例如原點,在垂直方向上沒有移動,但第一個分量為正值的向量會向上移動。在這裡,所有第一個分量為  的向量——即正方形的整個右側——都會受到相同程度的影響。更一般地說,位於同一垂線的向量會向上移動相同的距離,即它們向上移動的距離是其第一個分量的兩倍。由此產生的形狀(菱形)與正方形具有相同的底和高(因此面積相同),但直角消失了。
的向量——即正方形的整個右側——都會受到相同程度的影響。更一般地說,位於同一垂線的向量會向上移動相同的距離,即它們向上移動的距離是其第一個分量的兩倍。由此產生的形狀(菱形)與正方形具有相同的底和高(因此面積相同),但直角消失了。

作為對比,下一張圖片展示了由  表示的對映所產生的影響。在這種情況下,向量會根據其第二個分量受到影響。向量
表示的對映所產生的影響。在這種情況下,向量會根據其第二個分量受到影響。向量  會水平移動
會水平移動  的兩倍。
的兩倍。

由於這種作用,這種對映被稱為 **剪下**。
至此,我們已經涵蓋了擴張中四種類型元件的幾何效應 ,部分恆等投影
,部分恆等投影 和基本
和基本 。由於我們理解其組成部分,在某種意義上,我們也理解任何
。由於我們理解其組成部分,在某種意義上,我們也理解任何 的作用。為了說明這一斷言,回想一下,在一次線性對映下,子空間的像是一個子空間,因此由
的作用。為了說明這一斷言,回想一下,在一次線性對映下,子空間的像是一個子空間,因此由 表示的線性變換
表示的線性變換 將過原點的直線對映到過原點的直線。(像空間的維數不能大於定義域空間的維數,因此直線不能對映到例如平面。)我們將擴充套件這一點,證明任何直線,而不僅僅是過原點的直線,都會被
將過原點的直線對映到過原點的直線。(像空間的維數不能大於定義域空間的維數,因此直線不能對映到例如平面。)我們將擴充套件這一點,證明任何直線,而不僅僅是過原點的直線,都會被 對映到一條直線。證明很簡單,部分恆等投影
對映到一條直線。證明很簡單,部分恆等投影 和基本
和基本 每次將直線輸入轉換為直線輸出(驗證這四種情況是問題 6),因此它們的組合也保留了直線。因此,透過理解其組成部分,我們可以理解任意方陣
每次將直線輸入轉換為直線輸出(驗證這四種情況是問題 6),因此它們的組合也保留了直線。因此,透過理解其組成部分,我們可以理解任意方陣 ,因為我們可以證明關於它們的性質。
,因為我們可以證明關於它們的性質。
理解線性變換對 的幾何效應在數學中非常重要。以下是一個來自微積分的熟悉應用。左側是非線性函式
的幾何效應在數學中非常重要。以下是一個來自微積分的熟悉應用。左側是非線性函式 作用的影像。正如本主題開頭所述,總體而言,該對映的幾何效應是不規則的,因為在不同的定義域點上它具有不同的效應(例如,隨著定義域點
作用的影像。正如本主題開頭所述,總體而言,該對映的幾何效應是不規則的,因為在不同的定義域點上它具有不同的效應(例如,隨著定義域點 從
從 變為
變為 ,相關的值域點
,相關的值域點 開始下降,然後瞬間暫停,然後上升)。
開始下降,然後瞬間暫停,然後上升)。
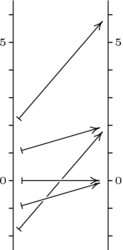
但在微積分中,我們不關注整個對映,而是關注對映的區域性效應。
在 處,導數為
處,導數為 ,因此在
,因此在 附近,我們有
附近,我們有 。
。
也就是說,在  的鄰域內,當將定義域對映到值域時,該對映會使值域增大
的鄰域內,當將定義域對映到值域時,該對映會使值域增大  倍——在區域性範圍內,它近似於一個伸縮變換。
倍——在區域性範圍內,它近似於一個伸縮變換。
下圖顯示了定義域中  的一個小區間,它被對映到值域中
的一個小區間,它被對映到值域中  的一個區間,該區間寬度是前者的三倍:
的一個區間,該區間寬度是前者的三倍: 。
。

(當以上圖形以傳統的笛卡爾座標系方式繪製時,關於  增速的上述句子通常會被表述為:導數
增速的上述句子通常會被表述為:導數  給出了該點
給出了該點  的切線的斜率。)
的切線的斜率。)
在更高維度中,這個想法是一樣的,但是近似值不僅僅是  到
到  的標量乘法情況。相反,對於一個函式
的標量乘法情況。相反,對於一個函式  和一個點
和一個點  ,導數被定義為一個線性對映
,導數被定義為一個線性對映  ,它最能近似地描述
,它最能近似地描述  在
在  附近的變化方式。因此,上述研究的幾何學也適用於這種情況。
附近的變化方式。因此,上述研究的幾何學也適用於這種情況。
我們將透過說明這種觀點如何使人們清楚地認識到一個關於導數的常常被誤解但非常重要的結果來結束本主題:兩個函式的複合函式的導數可以透過使用鏈式法則來組合它們的導數來計算。請記住(當兩個函式滿足適當條件時)

例如, 的導數是
的導數是  。這個組合是如何產生的呢?從複合函式作用的圖示可以看出來。
。這個組合是如何產生的呢?從複合函式作用的圖示可以看出來。
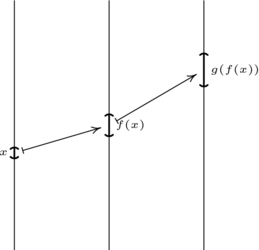
第一個對映  將
將  附近的鄰域按
附近的鄰域按

的因子進行膨脹,而第二個對映  將
將  附近的鄰域按
附近的鄰域按

的因子進行膨脹,因此,複合函式按這兩個因子的乘積進行膨脹。
在更高維空間中,表示函式在某點附近變化的對映是一個線性對映,它可以用矩陣表示。(因此,我們理解了高維導數的基本幾何意義;它們是膨脹、軸交換、剪下和投影的組合)。鏈式法則只是將這些矩陣相乘。
因此,線性對映  的幾何意義既簡單又實用。
的幾何意義既簡單又實用。
- 問題 2
伸縮、翻轉、斜切和投影的什麼組合產生了逆時針旋轉  弧度?
弧度?
- 問題 3
伸縮、翻轉、斜切和投影的什麼組合產生了對映  ,該對映由該矩陣相對於標準基表示?
,該對映由該矩陣相對於標準基表示?

- 問題 4
證明  的任何線性變換都是乘以標量
的任何線性變換都是乘以標量  的對映。
的對映。
- 問題 7
使用鏈式法則討論中出現的類似圖片來回答:如果函式 有逆函式,那麼該函式(區域性,近似)如何膨脹空間,以及它的逆函式如何膨脹空間之間存在什麼關係(當然,假設它有逆函式)?
有逆函式,那麼該函式(區域性,近似)如何膨脹空間,以及它的逆函式如何膨脹空間之間存在什麼關係(當然,假設它有逆函式)?
解答



















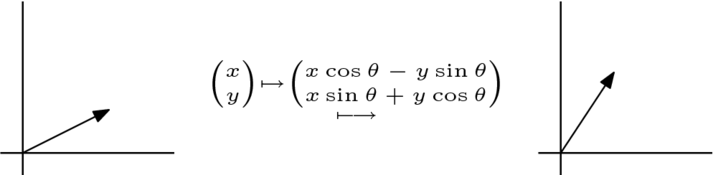











![{\displaystyle I{\xrightarrow[{}]{k\rho _{i}}}M_{i}(k)\qquad I{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}P_{i,j}\qquad I{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}C_{i,j}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8efb67d5d26695581b1ba19fa3f9d1f49e49f4ed)