線性代數/主題：投票悖論/解決方案

解決方案

問題 1

這裡有一個合理的投票者可能擁有迴圈偏好的方式。假設此投票者根據三個標準對每個候選人進行排名。

1. 製作一個表格，行標籤為“民主黨”、“共和黨”和“第三黨”，列標籤為“品格”、“經驗”和“政策”。在每一列中，將某個候選人排為最受歡迎，將另一個排為中間，並將剩下的排為最不受歡迎。
2. 在這個排名中，民主黨在（至少）三個標準中的兩個標準上是否比共和黨更受歡迎，反之亦然？共和黨是否比第三黨更受歡迎？
3. 剛剛構建的表格是否具有迴圈偏好順序？如果沒有，請建立一個具有迴圈偏好順序的表格。

因此，投票者可能對候選人具有迴圈偏好。然而，上面描述的悖論是，即使每個投票者都有一個直線偏好列表，整個群體仍然可能出現迴圈偏好。

答案

這是一個導致單個投票者非理性偏好順序的示例。

	品格	經驗	政策
民主黨	最受歡迎	中間	最不受歡迎
共和黨	中間	最不受歡迎	最受歡迎
第三黨	最不受歡迎	最受歡迎	中間

民主黨在品格和經驗方面比共和黨更受歡迎。共和黨在品格和政策方面比第三黨更受歡迎。而第三黨在經驗和政策方面比民主黨更受歡迎。

問題 2

計算分解表中的值。

答案

首先，將$D>R>T$分解與主題中完成的相反$T>R>D$投票者的分解進行比較。

${\begin{pmatrix}-1\\1\\1\end{pmatrix}}={\frac {1}{3}}\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\1\\0\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\0\\1\end{pmatrix}}\quad {\text{and}}\quad {\begin{pmatrix}1\\-1\\-1\end{pmatrix}}=d_{1}\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}+d_{2}\cdot {\begin{pmatrix}-1\\1\\0\end{pmatrix}}+d_{3}\cdot {\begin{pmatrix}-1\\0\\1\end{pmatrix}}$

顯然，第二個是第一個的負數，所以$d_{1}=-1/3$, $d_{2}=-2/3$, 以及$d_{3}=-2/3$。此原則適用於任何一對相反的投票者，因此我們只需對第二行的一個投票者和第三行的一個投票者進行計算。對於第二行中的正向投票者，

${\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\c_{1}&+&c_{2}&&&=&1\\c_{1}&&&+&c_{3}&=&-1\end{array}}\;{\xrightarrow[{-\rho _{1}+\rho _{3}}]{-\rho _{1}+\rho _{2}}}\;{\xrightarrow[{}]{(-1/2)\rho _{2}+\rho _{3}}}\;{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\&&2c_{2}&+&c_{3}&=&0\\&&&&(3/2)c_{3}&=&-2\end{array}}$

給出 $c_{3}=-4/3$，$c_{2}=2/3$，以及 $c_{1}=1/3$。對於第三行中的一個正面投票者，

${\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\c_{1}&+&c_{2}&&&=&-1\\c_{1}&&&+&c_{3}&=&1\end{array}}\;{\xrightarrow[{-\rho _{1}+\rho _{3}}]{-\rho _{1}+\rho _{2}}}\;{\xrightarrow[{}]{(-1/2)\rho _{2}+\rho _{3}}}\;{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\&&2c_{2}&+&c_{3}&=&-2\\&&&&(3/2)c_{3}&=&1\end{array}}$

給出 $c_{3}=2/3$，$c_{2}=-4/3$，以及 $c_{1}=1/3$。

問題 3

對於政治學班的模擬選舉，是否發生了相反偏好排序的抵消？剩下的偏好是來自表格的前三行還是後三行？

答案

模擬選舉對應於上面投票偏好表中顯示的方式，抵消之後的結果是第二張表。

正面傾向     負面傾向     $D>R>T$   5 票   $T>R>D$   2 票   $R>T>D$   8 票   $D>T>R$   4 票   $T>D>R$   8 票   $R>D>T$   2 票

正面傾向     負面傾向     $D>R>T$   3 票   $T>R>D$   –   $R>T>D$   4 票   $D>T>R$   –   $T>D>R$   6 票   $R>D>T$   –

所有三者都來自桌子的同一側（左側），正如本主題的結果所說必須發生的那樣。現在可以使用取消的數字進行選舉計票

$3\cdot \,$ $+4\cdot \,$$+6\cdot$$\,=\,$

得到相同的結果。

問題 4

上面證明的必要條件——投票悖論只有在取消後剩餘的所有三個偏好列表具有相同旋轉時才會發生——不是充分的。

1. 繼續證明中考慮的正迴圈情況，使用兩個不等式 $0\leq a-b+c$ 和 $0\leq -a+b+c$ 來證明 $|a-b|\leq c$.
2. 還需證明 $c\leq a+b$，因此 $|a-b|\leq c\leq a+b$.
3. 舉一個投票的例子，其中存在多數迴圈，並且新增一個具有相同旋轉的投票者會導致迴圈消失。
4. 相反的情況會發生嗎？新增一個具有“錯誤”旋轉的投票者會導致迴圈出現嗎？
5. 給出獲得多數迴圈的必要且充分的條件。

答案

1. 這兩個可以改寫成 $-c\leq a-b$ 和 $-c\leq b-a$。無論是 $a-b$ 還是 $b-a$ 都是非正數，因此 $-c\leq -|a-b|$，如所要求的。
2. 這是從假設 $0\leq a+b-c$ 中直接得出的。
3. 一個簡單的例子是從零選民選舉開始，然後新增任何一個選民。一個更有趣的例子是，取政治學模擬選舉，並新增兩個 $T>D>R$ 選民（他們可以一次新增一個，以滿足問題中“新增一個選民”的標準）。觀察到，這些額外的選民具有正旋度，這與原始模擬選舉中抵消後剩餘的票數的旋度相同。這是選民的表格結果，旁邊是抵消後的結果。

   正面傾向     負面傾向     $D>R>T$   5 票   $T>R>D$   2 票   $R>T>D$   8 票   $D>T>R$   4 票   $T>D>R$   10 位選民   $R>D>T$   2 票

   正面傾向     負面傾向     $D>R>T$   3 票   $T>R>D$   –   $R>T>D$   4 票   $D>T>R$   –   $T>D>R$   8 票   $R>D>T$   –

   使用抵消後的數字的選舉結果如下。

   $3\cdot \,$$\,+4\cdot \,$$\,+8\cdot \,$$\,=\,$

   多數迴圈確實消失了。

4. 其中一個條件是，抵消後，所有三個值都為非負數，或者所有三個值都為非正數，並且：$|c|<|a+b|$ 和 $|b|<|a+c|$ 和 $|a|<|b+c|$。這是從下圖得出的。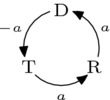

   $\,+\,$$\,+\,$$\,=\,$

問題 5

由於我們要求投票者的列表必須是合理的，因此單人投票選舉不可能出現多數迴圈。

1. 證明雙人投票選舉可能出現多數迴圈。（如果所有三個組的總數都為非負數或所有三個組的總數都為非正數，則我們認為群體偏好為多數迴圈——也就是說，我們允許群體偏好中存在零。）
2. 證明對於任何大於 1 的投票人數，存在涉及該人數投票的選舉，從而導致多數迴圈。

答案

1. 雙人投票選舉可以透過兩種方式出現多數迴圈。首先，這兩個投票者可以是相反的，在抵消後導致平凡選舉（所有為零的多數迴圈）。其次，這兩個投票者可以有相同的旋轉，但來自不同的行，如這裡所示。

   $1\cdot \,$$\,+1\cdot \,$$\,+0\cdot \,$$\,=\,$

2. 有兩種情況。偶數個投票者可以平均分成相反的兩個部分，例如，一半投票者是 $D>R>T$ 另一半是 $T>R>D$。然後抵消得到平凡選舉。如果投票人數大於 1 且為奇數（形如 $2k+1$ 其中 $k>0$）那麼使用證明中的迴圈圖，

   $\,+\,$$\,+\,$$\,=\,$

   我們可以取 $a=k$ 和 $b=k$ 以及 $c=1$。因為 $k>0$，這是一個多數迴圈。

問題 6

令 $U$ 是 $\mathbb {R} ^{3}$ 的一個子空間。證明向量集合 $U^{\perp }=\{{\vec {v}}\,{\big |}\,{\vec {v}}\cdot {\vec {u}}=0{\text{ for all }}{\vec {u}}\in U\}$，即與 $U$ 中每個向量垂直的向量，也是 $\mathbb {R} ^{3}$ 的一個子空間。

答案

它是非空的，因為它包含零向量。為了證明它在兩個成員的線性組合下是封閉的，假設 ${\vec {v}}_{1}$ 和 ${\vec {v}}_{2}$ 在 $U^{\perp }$ 中，並考慮 $c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}$。對於任何 ${\vec {u}}\in U$，

$(c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2})\cdot {\vec {u}}=c_{1}({\vec {v}}_{1}\cdot {\vec {u}})+c_{2}({\vec {v}}_{2}\cdot {\vec {u}})=c_{1}\cdot 0+c_{2}\cdot 0=0$

因此 $c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}\in U^{\perp }$.