線性代數/主題：投票悖論

想象一下，一個學習美國總統選舉過程的政治學班級舉行了一次模擬選舉。學生被要求按從最喜歡到最不喜歡的順序，對來自民主黨、共和黨和第三黨的候選人進行排名，結果如下 ($>$ 表示“比……更受歡迎”)。

偏好順序	具有該偏好的人數
民主黨 > 共和黨 > 第三黨	5
民主黨 > 第三黨 > 共和黨	4
共和黨 > 民主黨 > 第三黨	2
共和黨 > 第三黨 > 民主黨	8
第三黨 > 民主黨 > 共和黨	8
第三黨 > 共和黨 > 民主黨	2
總計	29

整個群體對候選人的偏好是什麼？

總體而言，該群體對民主黨比共和黨更喜愛，共五票之差；17 名選民將民主黨排在共和黨之上，而 12 名選民則相反。而且，該群體總體上更喜愛共和黨人而不是第三黨的候選人，共 15 票對 14 票。但是，奇怪的是，該群體也更喜愛第三黨人而不是民主黨人，共 18 票對 11 票。

‎

這是一個投票悖論的例子，具體來說，是一個多數迴圈。

對投票悖論的研究部分是因為它們對實際政治的影響。例如，老師可以透過首先讓班級在共和黨和第三黨之間選擇，然後再讓班級在該競賽的獲勝者（共和黨）和民主黨之間選擇，從而操縱班級選擇民主黨為總體獲勝者。透過類似的操縱，其他兩名候選人中的任何一個都可以成為獲勝者。（在本主題中，我們將堅持三名候選人的選舉，但類似的結果適用於更大的選舉。）

投票悖論也僅僅因為它們在數學上很有趣而被研究。 一個有趣的地方是，儘管每個選民的偏好列表都是理性的——以直線的順序排列，但該群體整體上的多數迴圈仍然發生了。也就是說，多數迴圈似乎是在聚合中產生的，而沒有出現在聚合的元素（偏好列表）中。然而，最近，線性代數被用來 (Zwicker 1991) 論證，實際上每個選民的列表中都存在著迴圈偏好的趨勢，並且當這種趨勢的加總比抵消多時，它就會顯現出來。

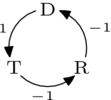
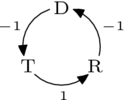
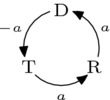
為了論證這一點，將選項簡寫為 $D$、$R$ 和 $T$，我們可以描述一個偏好順序為 $D>R>T$ 的選民是如何對上述迴圈做出貢獻的。

(負號在這裡是因為箭頭描述的是 $T$ 比 $D$ 更受歡迎，但該選民更喜歡它們的反方向。) 其他偏好列表的描述在下面的投票偏好表格中。

現在，要進行選舉，我們將這些描述線性組合起來；例如，政治學模擬選舉

$5\cdot \,$$\,+4\cdot \,$$\,+\cdots +2\cdot \,$

產生了前面顯示的迴圈群體偏好。

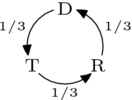
當然，取線性組合屬於線性代數。上面的迴圈記號具有提示性，但並不方便，因此我們暫時切換到使用列向量，從$D$ 開始，並以逆時針方向取迴圈中的數字。因此，模擬選舉和單個$D>R>T$ 投票將以這種方式表示。

${\begin{pmatrix}7\\1\\5\end{pmatrix}}\quad {\text{and}}\quad {\begin{pmatrix}-1\\1\\1\end{pmatrix}}$

我們將把投票向量分解成兩部分，一部分是迴圈的，另一部分是非迴圈的。對於第一部分，我們說一個向量是純迴圈的，如果它在這個子空間中$\mathbb {R} ^{3}$.

$C=\{{\begin{pmatrix}k\\k\\k\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}=\{k\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}$

對於第二部分，考慮子空間（參見問題 6），該子空間包含與 $C$ 中所有向量垂直的向量。

$C^{\perp }=\{{\begin{pmatrix}c_{1}\\c_{2}\\c_{3}\end{pmatrix}}\,{\big |}\,{\begin{pmatrix}c_{1}\\c_{2}\\c_{3}\end{pmatrix}}\cdot {\begin{pmatrix}k\\k\\k\end{pmatrix}}=0{\text{ for all }}k\in \mathbb {R} \}$

$=\{{\begin{pmatrix}c_{1}\\c_{2}\\c_{3}\end{pmatrix}}\,{\big |}\,c_{1}+c_{2}+c_{3}=0\}=\{c_{2}{\begin{pmatrix}-1\\1\\0\end{pmatrix}}+c_{3}{\begin{pmatrix}-1\\0\\1\end{pmatrix}}\,{\big |}\,c_{2},c_{3}\in \mathbb {R} \}$

(讀作“$C$ 垂直”。）因此，我們得到了$\mathbb {R} ^{3}$ 的這個基。

$\langle {\begin{pmatrix}1\\1\\1\end{pmatrix}},{\begin{pmatrix}-1\\1\\0\end{pmatrix}},{\begin{pmatrix}-1\\0\\1\end{pmatrix}}\rangle$

我們可以根據這個基表示投票，從而將投票分解為迴圈部分和非迴圈部分。（對於學習過本章可選章節的讀者注意：即，空間是$C$ 和$C^{\perp }$ 的直和。）

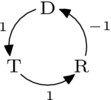
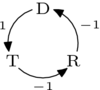
例如，考慮上面討論的$D>R>T$ 投票者。用基表示很容易找到，

${\begin{array}{rcl}{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&-1\\c_{1}&+&c_{2}&&&=&1\\c_{1}&&&+&c_{3}&=&1\end{array}}&{\xrightarrow[{-\rho _{1}+\rho _{3}}]{-\rho _{1}+\rho _{2}}}\;{\xrightarrow[{}]{(-1/2)\rho _{2}+\rho _{3}}}&{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&-1\\&&2c_{2}&+&c_{3}&=&2\\&&&&(3/2)c_{3}&=&1\end{array}}\end{array}}$

因此 $c_{1}=1/3$，$c_{2}=2/3$，以及 $c_{3}=2/3$。然後

${\begin{pmatrix}-1\\1\\1\end{pmatrix}}={\frac {1}{3}}\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\1\\0\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\0\\1\end{pmatrix}}={\begin{pmatrix}1/3\\1/3\\1/3\end{pmatrix}}+{\begin{pmatrix}-4/3\\2/3\\2/3\end{pmatrix}}$

給出迴圈部分和非迴圈部分的期望分解。

$\,=\,$$\,+\,$

因此，這個 $D>R>T$ 選民的理性偏好列表確實可以被看作具有一個迴圈部分。

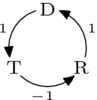
這個 $T>R>D$ 選民與我們剛才考慮的選民相反，因為 "$>$" 符號顛倒了。這個選民的分解

$\,=\,$$\,+\,$

表明這些相反的偏好具有相反的分解。 我們說第一個選民具有正的**自旋**，因為迴圈部分與我們為箭頭選擇的方向一致，而第二個選民的自旋為負。

這些相反的選民互相抵消的事實反映在他們的投票向量加起來為零的事實。這表明了一種計算選舉結果的替代方法。我們可以先儘可能地抵消相反的偏好列表，然後透過新增剩下的列表來確定結果。

下表中的行包含三對相反的偏好列表。列根據自旋對這些對進行分組。例如，第一行包含我們剛剛考慮的兩個選民。

投票偏好

正號	負自旋
民主黨 > 共和黨 > 第三方 $\,=\,$$\,+\,$	第三 > 共和黨 > 民主黨 $\,=\,$$\,+\,$
共和黨 > 第三 > 民主黨 $\,=\,$$\,+\,$	民主黨 > 第三 > 共和黨 $\,=\,$$\,+\,$
第三 > 民主黨 > 共和黨 $\,=\,$$\,+\,$	共和黨 > 民主黨 > 第三方 $\,=\,$$\,+\,$

如果我們像上面描述的那樣進行選舉，那麼在儘可能多地取消相反的投票對後，將剩下三組偏好列表，一組來自第一行，一組來自第二行，一組來自第三行。我們將最後證明，只有當這三組的自旋方向一致時，才會出現投票悖論。也就是說，為了出現投票悖論，這三個剩餘的集合必須全部來自表格的左側或全部來自右側（見 問題 3）。這表明，多數迴圈與我們使用的分解之間存在某種聯絡——只有當迴圈偏好的趨勢相互強化時，才會出現投票悖論。

為了證明，假設已經取消了相反的偏好順序，並且我們從三行中的每一行都剩下了一組偏好列表。考慮這三個的總和（這裡，數字 $a$，$b$，和 $c$ 可以是正數、負數或零）。

$\,+\,$$\,+\,$$\,=\,$

當右邊的三個數字 $a-b+c$、$a+b-c$ 和 $-a+b+c$ 都是非負數或都是非正數時，就會出現投票悖論。在左邊，三個數字中的至少兩個，$a$ 和 $b$ 以及 $c$，都是非負數或都是非正數。我們可以假設它們是 $a$ 和 $b$。這使得有四種情況：迴圈是非負數，並且 $a$ 和 $b$ 是非負數，迴圈是非正數，並且 $a$ 和 $b$ 是非正數等等。我們只做第一種情況，因為第二種情況類似，而另外兩種情況也很容易。

所以假設迴圈是非負數，並且 $a$ 和 $b$ 是非負數。條件 $0\leq a-b+c$ 和 $0\leq -a+b+c$ 相加得到 $0\leq 2c$，這意味著 $c$ 也是非負數，如預期的那樣。這結束了證明。

這個結果只說明，所有三個旋轉都朝同一方向是一個多數迴圈的必要條件。它不是充分的；見 問題 4。

投票理論及其相關主題是當前研究的課題。有許多有趣的成果，最引人注目的成果是由 K. Arrow 提出的 (Arrow 1963)，他因這部分工作而獲得了諾貝爾獎，表明沒有投票系統是完全公平的（對於“公平”的合理定義而言）。有關更多資訊，一些好的入門文章是 (Gardner 1970)、(Gardner 1974)、(Gardner 1980) 和 (Neimi & Riker 1976)。最近的一本相當易讀的書籍是 (Taylor 1995)。在 (Poundstone 2008) 中給出的來自美國政治史的眾多案例表明，在實踐中操縱這些悖論是司空見慣的事情（並且作者提出了一種解決方案）。

本主題主要摘自 (Zwicker 1991)。（作者注：我要感謝 Zwicker 教授的友好和富有啟發性的討論。）

練習

問題 1

這是一個投票者可能具有迴圈偏好的合理方式。假設該投票者根據三個標準對每個候選人進行排名。

1. 建立一個表格，其中行標為“民主黨”、“共和黨”和“第三黨”，列標為“品格”、“經驗”和“政策”。在每列中，將某個候選人排名為最受歡迎，將另一個候選人排名為中等，並將剩下的候選人排名為最不受歡迎。
2. 在這個排名中，民主黨是否在（至少）三個標準中的兩個標準中優於共和黨，反之亦然？共和黨是否優於第三黨？
3. 剛剛構建的表格是否有迴圈偏好順序？如果沒有，請建立一個有迴圈偏好順序的表格。

因此，投票者可能在候選人之間具有迴圈偏好。然而，上面描述的悖論是，即使每個投票者都擁有一個直線偏好列表，整個群體仍然可能出現迴圈偏好。

問題 2

計算分解表格中的值。

問題 3

對政治學課程模擬選舉進行相反偏好順序的抵消。所有剩餘的偏好是否都來自表格的左三行或來自右邊？

問題 4

上面證明的必要條件——投票悖論僅在抵消後剩餘的所有三個偏好列表具有相同的旋轉方向時才會發生——不是也充分的。

1. 繼續在證明中考慮的正迴圈情況，使用兩個不等式$0\leq a-b+c$ 和 $0\leq -a+b+c$ 來證明 $|a-b|\leq c$。
2. 還要證明 $c\leq a+b$，因此證明 $|a-b|\leq c\leq a+b$。
3. 給出一個有多數迴圈的投票示例，以及新增一個具有相同旋轉方向的投票者導致迴圈消失的情況。
4. 是否可能發生相反的情況；新增一個具有“錯誤”旋轉方向的投票者會導致迴圈出現？
5. 給出一個既必要又充分的條件來獲得多數迴圈。

問題 5

單人投票選舉不可能有多數迴圈，因為我們規定了投票者列表必須是理性的。

1. 證明二人投票選舉可能具有多數迴圈。（如果所有三個組總和非負，或者所有三個組總和非正，我們認為群體偏好是多數迴圈——也就是說，我們允許群體偏好中的一些為零。）
2. 證明對於大於 1 的任何投票者數量，都存在一個涉及該數量投票者的選舉，其結果是多數迴圈。

問題 6

令 $U$ 是 $\mathbb {R} ^{3}$ 的一個子空間。證明向量集合 $U^{\perp }=\{{\vec {v}}\,{\big |}\,{\vec {v}}\cdot {\vec {u}}=0{\text{ for all }}{\vec {u}}\in U\}$，它與 $U$ 中的每個向量垂直也是 $\mathbb {R} ^{3}$ 的一個子空間。

解答

參考文獻

• Arrow, J. (1963), 社會選擇與個人價值, Wiley.
• Gardner, Martin (1970 年 4 月)，“數學遊戲，太陽系中嵌入的一些數學奇事”，科學美國人：108-112.
• Gardner, Martin (1974 年 10 月)，"數學遊戲：從非傳遞關係中產生的悖論情況"，科學美國人.
• Gardner, Martin (1980 年 10 月)，"數學遊戲：從計票到讓票數有效：選舉的數學"，科學美國人.
• Neimi, G.；Riker, W. (1976 年 6 月)，"投票制度的選擇"，科學美國人：21–27.
• Poundstone, W. (2008)，操縱選舉，希爾與王，ISBN 978-0-8090-4893-9.
• Taylor, Alan D. (1995)，數學與政治：策略、投票、權力和證明，施普林格出版社.
• Zwicker, S. (1991)，"投票者悖論、旋轉和博達計數"，數學社會科學，22：187–227