線性代數/主題：晶體

每個人都注意到食鹽是立方體形狀的。

值得注意的是，對立方體外形的解釋是最簡單的：內部形狀，即原子的排列方式，也是立方體形狀的。內部結構如下圖所示。食鹽是氯化鈉，圖中顯示的小球是鈉，大球是氯。（為了簡化檢視，只顯示了前、上、右邊的鈉和氯。）

當我們將少量食鹽散佈在桌面上時，我們看到的食鹽顆粒由許多重複的這種基本單元組成。也就是說，這些原子立方體堆疊起來，形成了我們看到的更大的立方體結構。像食鹽這樣的具有規則內部結構的固體被稱為晶體。

我們可以將注意力集中在正面上。在那裡，我們看到這種模式重複了很多次。

該單元格角之間的距離約為 3.34 埃（1 埃為$10^{-10}$ 米）。顯然，這個單位不適合描述晶格中的點。相反，我們自然地採用這種基底作為單位。

$\langle {\begin{pmatrix}3.34\\0\end{pmatrix}},{\begin{pmatrix}0\\3.34\end{pmatrix}}\rangle$

然後我們可以描述，例如，上面圖片中右上角的角為$3{\vec {\beta }}_{1}+2{\vec {\beta }}_{2}$.

另一個常見的晶體是鉛筆芯。它是石墨，由以這種形狀排列的碳原子構成。

這是一層石墨。一塊石墨由許多層這種平面堆疊而成。（平面之間的化學鍵比平面內部的鍵弱得多，這解釋了為什麼石墨可以書寫——它可以被剪下，使得平面滑落並留在紙上。）可以透過將六邊形環分解成三個區域來形成一個方便的長度單位，這三個區域是這個晶胞的旋轉。

        

那麼，一個自然基底將由形成該晶胞邊的向量組成。底部和斜面的距離是$1.42$ 埃，所以這個

$\langle {\begin{pmatrix}1.42\\0\end{pmatrix}},{\begin{pmatrix}1.23\\.71\end{pmatrix}}\rangle$

是一個好的基底。

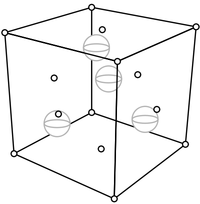
方便基底的選擇可以擴充套件到三維空間。另一種由碳形成的常見晶體是金剛石。與食鹽一樣，它也是由立方體構成，但每個立方體內的結構比食鹽的複雜。除了每個角都有一個碳原子外，

每個面的中間也有一個碳原子。

（為了清楚地顯示新增的面碳原子，角碳原子已縮減為點。）立方體內部還有四個碳原子，兩個位於底部向上四分之一處，另外兩個位於頂部向下四分之一處。

（與以前一樣，此處先前顯示的碳原子已縮減為點。）立方體沿任何邊的距離為$2.18$ 埃。因此，描述碳原子位置及其之間鍵的自然基底是這個。

$\langle {\begin{pmatrix}2.18\\0\\0\end{pmatrix}},{\begin{pmatrix}0\\2.18\\0\end{pmatrix}},{\begin{pmatrix}0\\0\\2.18\end{pmatrix}}\rangle$

即使這裡給出的幾個例子也表明，晶體的結構非常複雜，需要一個有組織的系統來給出原子的位置以及它們是如何化學鍵合的。用於組織的工具之一是一個方便的基底。這種基底的應用很簡單，但它顯示了一個基底概念自然產生的環境。本章的工作只是將這個簡單的概念發展起來。

練習

問題 1

一小塊食鹽的一面有多少個基本區域？ (用尺子可以估計該面是一個邊長為 $0.1$ 釐米的正方形。)

問題 2

在石墨的圖片中，想象我們對一個點 $5.67$ 埃向上和 $3.14$ 埃從原點出發感興趣。

1. 用石墨給出的基底來表示該點。
2. 該點距離原點多少個六邊形形狀？
3. 用第二個基底表示該點，其中第一個基底向量相同，但第二個基底向量與第一個基底向量垂直（向上穿過平面），長度相同。

問題 3

給出金剛石立方體中原子在基底和埃中的位置。

問題 4

這說明了如何根據物質的晶體形狀計算出晶胞的尺寸（參見 Ebbing 1993, p. 462）。

1. 回想一下，一摩爾中有 $6.022\times 10^{23}$ 個原子（這是阿伏伽德羅常數）。從這一點出發，以及鉑的質量為 $195.08$ 克每摩爾，計算每個原子的質量。
2. 鉑在面心立方晶格中結晶，每個晶格點上都有原子，也就是說，它看起來像上面給出的金剛石晶體的中間圖片。找到每個晶胞中的鉑原子數（提示：將位於單個晶胞內的鉑原子分數加起來）。
3. 據此，找出晶胞的質量。
4. 鉑晶體的密度為 $21.45$ 克每立方厘米。據此，以及晶胞的質量，計算出晶胞的體積。
5. 找出每條邊的長度。
6. 描述一個自然的三維基底。

解決方案

參考資料

• Ebbing, Darrell D. (1993), General Chemistry (Fourth ed.), Houghton Mifflin.