電子材料/受限粒子/一維有限勢阱

我們已經看到了無限勢阱的結果，但這在現實生活中是不可能存在的 - 一個點不可能相對於另一個點具有無限的勢能。讓我們考慮對稱有限勢阱，對吧。如果阱以原點為中心，在數學上更容易處理。如前所述，阱內的勢能（在-L和L之間）為0，但在阱外，它是一個有限值V（兩側相等）

$V\left(x\right)={\begin{cases}V,\quad x<-L\\0,\quad -L\leq x\leq L\\V,\quad x>L\end{cases}}$

由於井外的勢能是有限的，即使電子的勢能小於V，電子也可能從井中逃逸（量子隧穿），因此我們預計會看到一個在井邊界處不為零的波函式。

讓我們將我們的波函式分成三部分，每一側一部分，井內一部分

$\psi \left(x\right)={\begin{cases}\psi _{1}\left(x\right),&\quad x<-L\\\psi _{2}\left(x\right),&\quad -L\leq x\leq L\\\psi _{3}\left(x\right),&\quad x>L\end{cases}}$

我們將使用薛定諤方程分別求解每個波函式

[一維時間無關薛定諤方程]

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\psi \left(x\right)+V(x)\psi =E\psi$

井內

在井內，勢能為零，因此我們可以將薛定諤方程改寫為：

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\psi _{2}\left(x\right)=E\psi _{2}$

重新排列，

${{d^{2}} \over {dx^{2}}}\psi _{2}\left(x\right)=-{{2mE} \over \hbar ^{2}}\psi _{2}\left(x\right)$

回想一下，能量由下式給出

$E\,$	$=T\left(x\right)+V\left(x\right)\,$
	$={{\hbar ^{2}k^{2}} \over {2m}}$

將E代入我們的微分方程得到

${{d^{2}\psi _{2}\left(x\right)} \over {dx^{2}}}=-k^{2}\psi _{2}\left(x\right)$

現在這是一個標準形式的二階微分方程。通解由下式給出：

[ψ_2的通解]

$\psi _{2}\left(x\right)=A\sin {kx}+B\cos {kx}$

這裡的能量是

$E={\frac {k^{2}\hbar ^{2}}{2m}}$

在這個通解中，A 和 B 可以是任何複數，k 可以是任何實數。

井外

我們現在來看波函式ψ₁所在的區域，即左側區域。井右側區域將會有相同的推導。對於井左側的外部區域，由於勢能是恆定的，V(x) = V，我們的薛定諤方程變為

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\psi _{1}\left(x\right)=(E-V)\psi _{1}$

有兩個可能的解集，取決於E 小於 V（粒子束縛在勢阱中）還是 E 大於 V（粒子是自由的）。

非束縛態

對於自由粒子，E > V，令

$\kappa ^{2}={\frac {2m(E-V)}{\hbar ^{2}}}$

得到

${\frac {d^{2}}{dx^{2}}}\psi _{1}\left(x\right)=-\kappa ^{2}\psi _{1}$

具有與井內相同的解形式

$\psi _{1}=C\sin(\kappa x)+D\cos(\kappa x)\quad$

束縛態

此分析將首先關注束縛態，其中E-V。令

$\alpha ^{2}={\frac {2m(V-E)}{\hbar ^{2}}}$

得到

${\frac {d^{2}}{dx^{2}}}\psi _{1}\left(x\right)=\alpha ^{2}\psi _{1}\left(x\right)$

其中通解是指數函式

$\psi _{1}\left(x\right)=Fe^{-\alpha x}+Ge^{\alpha x}\,\!$

類似地，對於井外的另一個區域

$\psi _{3}\left(x\right)=He^{-\alpha x}+Ie^{\alpha x}\,\!$

現在，為了找到手頭問題的特定解，我們必須指定適當的邊界條件，並找到滿足這些條件的 *A* 、*B* 、*F* 、*G* 、*H* 和 *I* 的值。

尋找束縛態的波函式

薛定諤方程的解必須是連續的，並且是連續可微的。這些要求是先前推導的微分方程的邊界條件。

在這種情況下，有限勢阱是對稱的，因此可以透過選擇定義明確奇偶性的波函式來利用對稱性減少必要的計算。

總結前幾節

$\psi \left(x\right)={\begin{cases}\psi _{1}\left(x\right),&\quad x<-L\\\psi _{2}\left(x\right),&\quad -L\leq x\leq L\\\psi _{3}\left(x\right),&\quad x>L\end{cases}}$

我們發現了束縛態的波函式，$\psi _{1},\psi _{2}\,\!$ 和 $\psi _{3}\,\!$ 為

$\psi _{1}\left(x\right)=Fe^{-\alpha x}+Ge^{\alpha x}\,\!$

$\psi _{2}\left(x\right)=A\sin(kx)+B\cos(kx)\quad$

$\psi _{3}\left(x\right)=He^{-\alpha x}+Ie^{\alpha x}\,\!$

其中

$k={\frac {\sqrt {2mE}}{\hbar }}$

$\alpha ={\frac {\sqrt {2m(V-E)}}{\hbar }}$

我們看到，當 *x* 趨於 $-\infty$ 時，*F* 項趨於無窮大。同樣，當 *x* 趨於 $+\infty$ 時，*I* 項趨於無窮大。由於波函式對於所有 *x* 必須是有限的，這意味著我們必須設定 *F* = *I* = 0，並且我們有

$\psi _{1}\left(x\right)=Ge^{\alpha x}\,\!$

$\psi _{2}\left(x\right)=A\sin(kx)+B\cos(kx)$

$\psi _{3}\left(x\right)=He^{-\alpha x}\,\!$

接下來，我們知道總的 $\psi \,\!$ 函式必須是連續的並且可微的。換句話說，函式的值及其導數必須在分割點匹配。

$\psi _{1}(-L)=\psi _{2}(-L)\,\!$		$\psi _{2}(L)=\psi _{3}(L)\,\!$
${\frac {d\psi _{1}}{dx}}(-L)={\frac {d\psi _{2}}{dx}}(-L)\,\!$		${\frac {d\psi _{2}}{dx}}(L)={\frac {d\psi _{3}}{dx}}(L)\,\!$

首先，我們需要回顧一下，必須存在具有明確定義的 奇偶性 的波函式解，奇數 **或** 偶數。由於正弦函式是奇函式，餘弦函式是偶函式，我們可以尋找阱中正弦或餘弦形式的波函式解。現在我們可以分別分析偶數和奇數波函式。將證明對於束縛態，偶數解和奇數解總是具有不同的能量。這意味著沒有簡併，因此沒有束縛本徵態是正弦和餘弦的線性組合，並且所有束縛態都具有明確定義的奇偶性。下面是一個圖，顯示了一個偶數奇偶性波函式和一個奇數奇偶性波函式。這些僅用於說明，並不一定與給定問題相關，它們旨在僅傳達波函式的對稱性。

偶數波函式

偶數解的波函式沒有奇數（正弦）分量，所以三個波函式現在是

$\psi _{1}\left(x\right)=Ge^{\alpha x}\,\!$

$\psi _{2}\left(x\right)=B\cos(kx)$

$\psi _{3}\left(x\right)=He^{-\alpha x}\,\!$

現在讓我們考慮在兩個“連線點”處要求波函式連續的條件

$Ge^{-\alpha L}=B\cos(-kL)\,$

$He^{-\alpha L}=B\cos(kL)\,$

由於餘弦函式是偶函式，這兩個方程具有相同的右手邊。因此我們有

$Ge^{-\alpha L}=He^{-\alpha L}\,$

$G=H\,$

邊界處導數連續的條件給了我們以下結果

$\alpha Ge^{-\alpha L}=-kB\sin(-kL)\,$

$\alpha He^{-\alpha L}=kB\sin(kL)\,$

鑑於 G 和 H 相等，我們現在可以將第二條件中的任何方程式除以第一條件中的任何方程式。我將選擇每個集合中的第一個方程式。

${\frac {\alpha Ge^{-\alpha L}}{Ge^{-\alpha L}}}={\frac {-kB\sin(-kL)}{B\cos(-kL)}}$

現在我們得到了 α 的表示式（回想一下，tan 函式是奇函式，因此負號相互抵消）。

$\alpha =k\tan \left(kL\right),$

其中

$k={\frac {\sqrt {2mE}}{\hbar }}$

$\alpha ={\frac {\sqrt {2m(V-E)}}{\hbar }}$

這可以簡化為以下方程式

${\frac {\alpha }{k}}=\tan \left(kL\right),$

${\sqrt {\frac {V-E}{E}}}=\tan \left({\frac {\sqrt {2mE}}{\hbar }}L\right)$

偶宇稱波函式存在於滿足此方程式的能量 (E) 處。此方程式非常難以解析求解，但可以很容易地數值求解或圖形求解。這將在後面完成。首先，我們將推匯出奇宇稱波函式。

奇波函式

奇解的波函式沒有偶數（餘弦）分量，因此三個波函式現在是

$\psi _{1}\left(x\right)=Ge^{\alpha x}\,\!$

$\psi _{2}\left(x\right)=A\sin(kx)$

$\psi _{3}\left(x\right)=He^{-\alpha x}\,\!$

現在讓我們考慮在兩個“連線點”處要求波函式連續的條件

$Ge^{-\alpha L}=A\sin(-kL)\,$

$-He^{-\alpha L}=A\sin(kL)\,$

由於正弦是奇函式，我們可以看到

$Ge^{-\alpha L}=-He^{-\alpha L}\,$

$G=-H\,$

邊界處導數連續的條件給了我們以下結果

$\alpha Ge^{-\alpha L}=kA\cos(-kL)\,$

$\alpha He^{-\alpha L}=kA\cos(kL)\,$

將第二組中的第一個方程式除以第一組中的第一個方程式（任何組合都可以），我們得到

${\frac {\alpha Ge^{-\alpha L}}{Ge^{-\alpha L}}}={\frac {kA\cos(-kL)}{A\sin(-kL)}}$

$\alpha =k\cot \left(-kL\right)\,$

並且因為 cot 是奇函式，

${\frac {\alpha }{k}}=-\cot \left(kL\right)$

${\sqrt {\frac {V-E}{E}}}=-\cot \left({\frac {\sqrt {2mE}}{\hbar }}L\right)$

當能量滿足此條件時，存在奇宇稱波函式。與偶波函式一樣，這個方程不容易解析求解，但可以圖形或數值求解。

能級圖解法

讓我們快速回顧一下我們的目標。我們希望找到電子在有限方勢阱中束縛態的能量。當滿足以下條件之一時，就會出現能級：

[偶波函式存在條件]

${\frac {\alpha }{k}}=\tan \left(kL\right)$

[奇波函式存在條件]

${\frac {\alpha }{k}}=-\cot \left(kL\right)$

我們可以將三個函式一起繪製在針對能量 *E* 的圖形上。條件在交叉點處滿足，如下所示。因此，我們可以透過讀取交叉點的能量來找到允許的能級。在我們繪製圖形之前，我們需要選擇系統的一些屬性。讓我們將阱的寬度設定為 0.4 奈米（*L* = 0.2 奈米），並將勢壘 *V* 設定為 75 電子伏特。

我們看到有六個允許的能級：偶波函式大約在 2、17 和 46 電子伏特處，奇波函式大約在 7.5、30 和 64.5 電子伏特處。這種方法提供了一種簡單的方法來找出有多少能級以及它們大致位於何處。雖然圖解法在理論上與任何方法一樣精確，但實際上可以使用純數值方法獲得更高的精度。

還要注意，無論勢壘多麼小，都將 *始終* 至少存在一個偶解，對應於第一個交點。奇解的存在取決於 V 的值。

能級數值方法

有許多數值方法可用於求解這些方程。雖然這些方程無法精確求解，但它們 *可以* 被微分。這意味著我們可以使用 牛頓-拉夫森 迭代，這些迭代通常收斂速度很快。透過使用圖解法對根的位置有一個大致的瞭解，我們可以為迭代選擇合適的起始值。

以下兩個方程是使用迭代求解的方程（牛頓-拉夫森方法需要一個等於零的函式）。

${\frac {\alpha }{k}}-\tan \left(kL\right)=0$

${\frac {\alpha }{k}}+\cot \left(kL\right)=0$

迭代需要這些方程的導數（除非由計算機自動完成），如下所示：

${\frac {-V}{2E^{2}{\sqrt {\frac {V-E}{E}}}}}-{\frac {Lm}{\hbar {\sqrt {2mE}}}}\sec ^{2}\left({\frac {L{\sqrt {2mE}}}{\hbar }}\right)$

${\frac {-V}{2E^{2}{\sqrt {\frac {V-E}{E}}}}}-{\frac {Lm}{\hbar {\sqrt {2mE}}}}\csc ^{2}\left({\frac {L{\sqrt {2mE}}}{\hbar }}\right)$

下表顯示了該系統中的六個能級、迭代的起始值以及能量（精確到小數點後五位）。

n	宇稱	起始值/eV	能量/eV
1	偶	2	1.89660
2	奇	8	7.56592
3	偶	17	16.93946
4	奇	30	29.87241
5	偶	46	46.05440
6	奇	64	64.60181

讓我們將這些值與無限方勢阱的前六個能級進行比較，我們之前已經瞭解瞭如何推匯出這些能級。

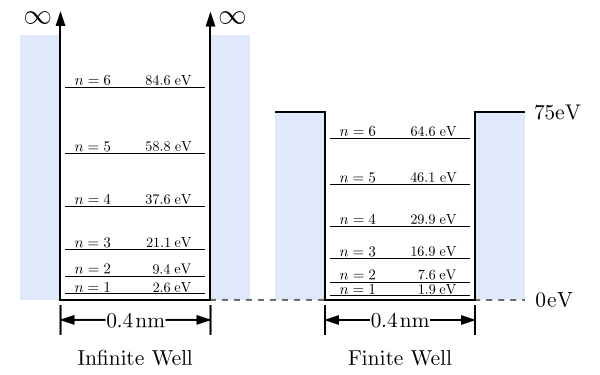
如您所見，有限勢阱中的能級低於無限勢阱中的能級。這是由於波函式擴充套件到勢阱的邊界之外，有效地導致了更大的盒子。由於更大的盒子會導致更低的能級，因此這是合理的。

查詢數值波函式

我們找到了評估有限勢阱中存在的能級的方法，這通常是唯一需要的的資訊，但我們也可以找到波函式的形狀。我們已經知道它的近似形狀——它在勢阱內是正弦形的，並在勢阱外呈指數衰減至零。

第一能級

讓我們從第一個（最低）能級開始，它是偶數。我們已經定義了波函式的分段如下

$\psi _{1}\left(x\right)=Ge^{\alpha x}\,\!$

$\psi _{2}\left(x\right)=B\cos(kx)$

$\psi _{3}\left(x\right)=He^{-\alpha x}\,\!$

現在我們知道能級，我們可以輕鬆計算k和α。這意味著我們只需要找到G，B和H。我們已經證明G=H。由於我們之後需要對波函式進行歸一化，因此我們可以在此時任意地調整函式的縮放比例而不會造成影響。讓我們將B的值設定為1。這樣我們只需要找到滿足連續邊界條件的G（=H）的值。

$\psi _{3}(L)=\psi _{2}(L)\,\!$

$Ge^{-\alpha L}=\cos(kL)\,$

重新排列，

$G={\frac {\cos(kL)}{e^{-\alpha L}}}$

第一能級上的k和α以及E的值

• E = 1.89660eV = 3.03868 × 10^-19 J
• k = 7.05548 × 10⁹
• α= 4.38034 × 10¹⁰

這使得

• G = 1014.31

現在我們可以將波函式相對於位置繪製出來。注意，我們還沒有進行歸一化，所以單位是任意的。

我們可以看到波函式明顯地延伸到經典禁區（藍色）。如果梯度的精確匹配難以理解，請記住正是這種條件導致了k和α的定義。但是，由於導致這一點的計算僅適用於有效的能量，如果你嘗試繪製非有效能量的波函式，你將得到一個連續（因為獲取G的方法強制執行這一點）但不是平滑的圖形，這意味著該解不適合物理系統。

因為我們沒有能量與圖形形狀之間的簡單關係（注意G作為E的相當複雜的函式而改變），我們無法找到一個易於表達的歸一化係數。但是，透過積分波函式的平方，我們仍然可以對其進行評估

$\int _{-\infty }^{\infty }|\psi (x)|^{2}dx=1$

$\int _{-\infty }^{-L}|\psi _{1}(x)|^{2}dx+\int _{-L}^{L}|\psi _{2}(x)|^{2}dx+\int _{L}^{\infty }|\psi _{3}(x)|^{2}dx=1$

$\psi _{0}^{2}\left[\int _{-\infty }^{-L}G^{2}e^{2\alpha x}dx+\int _{-L}^{L}\cos ^{2}(kx)dx+\int _{L}^{\infty }G^{2}e^{-2\alpha x}dx\right]=1$

這個積分非常簡單，得到以下歸一化係數

• ψ₀=66990.6

將此與無限勢阱的70710.7進行比較。記住在進行此積分時要考慮單位（通常是奈米會導致問題）。歸一化係數在這裡較低是有道理的，因為波函式擴充套件得更遠，因此當正弦曲線被縮放為1時，它的面積更大，這意味著它必須乘以更小的數字才能得到在某個地方找到粒子的單位機率。

第二能級

現在讓我們考慮第二個能級，它是奇數。波函式由下式給出

$\psi _{1}\left(x\right)=Ge^{\alpha x}\,\!$

$\psi _{2}\left(x\right)=A\sin(kx)$

$\psi _{3}\left(x\right)=He^{-\alpha x}\,\!$

其中G = -H。設定A=1，並繼續如上所述，我們得到以下結果

• E = 7.56592eV = 1.21219389 × 10^-18 J
• k = 1.40919 × 10¹⁰
• α= 7.99293 × 10⁹

這使得G為1432.53，並導致以下圖形

要獲得歸一化係數，我們輸入

$\int _{-\infty }^{\infty }|\psi (x)|^{2}dx=1$

$\int _{-\infty }^{-L}|\psi _{1}(x)|^{2}dx+\int _{-L}^{L}|\psi _{2}(x)|^{2}dx+\int _{L}^{\infty }|\psi _{3}(x)|^{2}dx=1$

$\psi _{0}^{2}\left[\int _{-\infty }^{-L}G^{2}e^{2\alpha x}dx+\int _{-L}^{L}\sin ^{2}(kx)dx+\int _{L}^{\infty }G^{2}e^{-2\alpha x}dx\right]=1$

這得到一個66849.7的歸一化係數。這略小於第一能級的係數。由於波函式進一步擴充套件到勢壘區域（在圖形中並不明顯，但可以觀察到），這是可以預期的。我們可以看到這種模式在所有六個能級中持續存在

n	宇稱	G	ψ0
1	偶	1014.31	66990.6
2	奇	1432.53	66849.7
3	偶	-1168.56	66575.5
4	奇	-615.794	66073.7
5	偶	194.185	65055.8
6	奇	25.2653	61954.1

無界狀態

對於一個粒子，其能量高於勢阱頂部的能量 V，也會有允許的能級。這些能級被稱為無束縛態，因為它們在阱外不會衰減到零。但是，它們肯定仍然受勢阱的影響。無束縛態也稱為連續態，因為與離散的束縛態不同，它們在滿足以下條件的連續能量範圍內都有解

$E>V\,$

回顧α的定義

$\alpha ={\frac {\sqrt {2m(V-E)}}{\hbar }}$

在無束縛態中，它是虛數，這意味著我們不能使用與束縛態相同的解法。如果你觀察圖形解，你會發現α/k的線在V處結束，這意味著在此點之後不再有有效的束縛態能級。

我們在本頁開頭看到，無束縛態在阱外的波函式為

$\psi _{1}\left(x\right)=C\sin(\kappa x)+D\cos(\kappa x)\quad$

其中

$\kappa ={\sqrt {\frac {2m(E-V))}{\hbar ^{2}}}}$

阱內的解與束縛態相同

$\psi _{2}\left(x\right)=A\sin {kx}+B\cos {kx}$

由於勢能圍繞原點對稱，因此對於無束縛態也必須有定義奇偶性的解，因此我們將選擇奇波函式和偶波函式的基底。與以前一樣，我們知道總波函式必須是連續且可微的。換句話說，函式值及其導數必須在分割點處匹配。

$\psi _{1}(-L)=\psi _{2}(-L)\,\!$		$\psi _{1}(L)=\psi _{2}(L)\,\!$
${\frac {d\psi _{1}}{dx}}(-L)={\frac {d\psi _{2}}{dx}}(-L)\,\!$		${\frac {d\psi _{1}}{dx}}(L)={\frac {d\psi _{2}}{dx}}(L)\,\!$

奇波函式

對於奇波函式，我們可以忽略$\psi _{2}$的餘弦項，但不能忽略$\psi _{1}$和$\psi _{3}$

$\psi _{2}\left(x\right)=A\sin {kx}\,\!$

$\psi _{1}\left(x\right)=C\sin {\kappa x}+D\cos {\kappa x}=C\sin {(\kappa x-\phi )}$

$\psi _{3}\left(x\right)=E\sin {\kappa x}+F\cos {\kappa x}=C\sin {(\kappa x+\phi )}$

$\psi _{1}$ 和 $\psi _{3}$ 本身不是奇函式，但對於所有 x 定義的通用函式 $\psi$ 是奇函式，注意到對於任何 $x_{0}>L$

$\psi _{1}\left(-x_{0}\right)=\psi _{3}\left(x_{0}\right)$

應用波函式連續性邊界條件，我們得到每個邊界處的相同結果。

$C\sin {(\kappa L+\phi )}=A\sin {kL}\,\!$

取導數並在 L 處要求連續性，我們得到

$\kappa C\cos {(\kappa L+\phi )}=kA\cos {kL}\,\!$

選擇具有已定義奇偶性的波函式將問題簡化為僅在一個點調整波函式及其導數的值（因為另一個點會產生相同的方程）。因此我們有兩個方程，三個變數。我們將選擇井外波函式的振幅 C 為單位。最後，我們將對整個一維有限井上的 $\psi$ 進行歸一化。

用波函式連續性匯出的方程除以導數連續性的方程

$\tan {(\kappa L+\phi )}={\frac {\kappa }{k}}\tan {kL}$

$\phi =\arctan {({\frac {\kappa }{k}}\tan {kL}})-\kappa L$

將相位 $\phi$ 代入 L 處的連續性方程，並取 C=1，我們得到

$A={\frac {\sin {(\kappa L+\phi )}}{\sin {kL}}}$

因此我們看到對於任何能量、井深和寬度，都存在奇波函式解。當

$\sin {kL}=0,\!$

時，在井上方存在共振。這類似於光學中的法布里-珀羅共振。

偶數波函式

與奇數波函式相同，我們可以忽略 $\psi _{2}$ 的正弦項，但不能忽略偶數波函式的 $\psi _{1}$ 和 $\psi _{3}$ 的正弦項。

$\psi _{2}\left(x\right)=B\cos {kx}\,\!$

$\psi _{1}\left(x\right)=C\sin {\kappa x}+D\cos {\kappa x}=D\cos {(\kappa x-\phi )}$

$\psi _{3}\left(x\right)=E\sin {\kappa x}+F\cos {\kappa x}=C\cos {(\kappa x+\phi )}$

應用波函式連續性邊界條件，我們得到每個邊界處的相同結果。

$C\cos {(\kappa L+\phi )}=B\cos {kL}\,\!$

取導數並在 L 處要求連續性，我們得到

$\kappa C\sin {(\kappa L+\phi )}=kA\sin {kL}\,\!$

用波函式連續性匯出的方程除以導數連續性的方程

$\tan {(\kappa L+\phi )}={\frac {k}{\kappa }}\tan {kL}$

$\phi =\arctan {({\frac {k}{\kappa }}\tan {kL}})-\kappa L$

將相位 $\phi$ 代入 L 處的連續性方程，並取 C=1，我們得到

$A={\frac {\cos {(\kappa L+\phi )}}{\cos {kL}}}$

因此，我們看到對於任何能量、阱深和寬度，都存在偶數波函式解。當

$\cos {kL}=0,\!$