偏微分方程/泊松方程

本章討論泊松方程

$\forall x\in \mathbb {R} ^{d}:-\Delta u(x)=f(x)$

假設 $f\in {\mathcal {C}}^{2}(\mathbb {R} ^{d})$，我們將透過分佈理論證明一個解公式，並且對於滿足一定性質邊界條件的域，我們甚至可以證明邊值問題的解公式。我們還會研究齊次泊松方程的解

$\forall x\in \mathbb {R} ^{d}:-\Delta u(x)=0$

齊次泊松方程的解稱為調和函式。

多維積分的重要定理

在第 2 節中，我們看到了萊布尼茨積分法則，在第 4 節中，我們看到了富比尼定理。在本節中，我們將回顧多維積分中其他的一些定理，這些定理對於將分佈理論應用於偏微分方程至關重要。不會給出證明，因為理解這些定理的證明對於理解本華夏公益教科書並不重要。唯一例外是定理 6.3，它由定理 6.2 推匯出。該定理的證明是一道習題。

定理 6.2:（散度定理）

令 $K\subset \mathbb {R} ^{d}$ 是一個具有光滑邊界的緊集。如果 $\mathbf {V} :K\to \mathbb {R} ^{d}$ 是一個向量場，則

$\int _{K}\nabla \cdot \mathbf {V} (x)dx=\int _{\partial K}\nu (x)\cdot \mathbf {V} (x)dx$

, 其中 $\nu :\partial K\to \mathbb {R} ^{d}$ 是外法向量。

定理 6.3:（多維分部積分）

令 $K\subset \mathbb {R} ^{d}$ 是一個具有光滑邊界的緊集。如果 $f:K\to \mathbb {R}$ 是一個函式，並且 $\mathbf {W} :K\to \mathbb {R} ^{d}$ 是一個向量場，則

$\int _{K}f(x)\nabla \cdot \mathbf {W} (x)dx=\int _{\partial K}f(x)\nu (x)\cdot \mathbf {W} (x)dx-\int _{K}\mathbf {W} (x)\cdot \nabla f(x)dx$

, 其中 $\nu :\partial K\to \mathbb {R} ^{d}$ 是外法向量。

證明: 見練習 1。

d 維球體的體積和表面積

定義 6.5:

Gamma 函式 $\Gamma :\mathbb {R} _{>0}\to \mathbb {R}$ 定義為

$\Gamma (x):=\int _{0}^{\infty }s^{x-1}e^{-s}ds$

Gamma 函式滿足以下等式

定理 6.6:

$\forall x\in \mathbb {R} _{>0}:\Gamma (x+1)=x\Gamma (x)$

證明:

$\Gamma (x+1)=\int _{0}^{\infty }s^{x}e^{-s}ds{\overset {\text{integration by parts}}{=}}\underbrace {-s^{x}e^{-s}{\big |}_{s=0}^{s=\infty }} _{=0}-\int _{0}^{\infty }-xs^{x-1}e^{-s}ds=x\Gamma (x)$

$\Box$

如果 Gamma 函式向右平移 1 個單位，它就是階乘函式的插值（見練習 2）

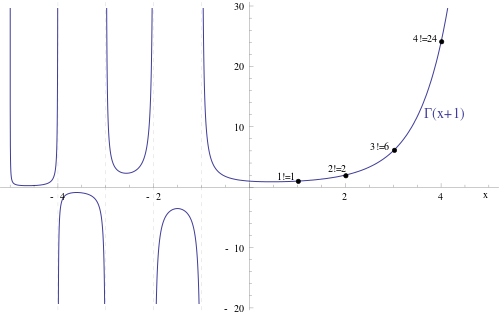
如上圖所示，Gamma 函式在負數上也有值。 這是因為上圖顯示的是 Gamma 函式的一種自然延拓，這種延拓可以透過複分析來構造。

定義和定理 6.7:

$d$ 維球面座標，由 $\Psi :(0,\infty )\times (0,2\pi )\times (-\pi /2,\pi /2)^{d-2}\to \mathbb {R} ^{d}\setminus \{(x_{1},\ldots ,x_{d})\in \mathbb {R} ^{d}:x_{1}\geq 0\wedge x_{2}=0\}$

$\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})={\begin{pmatrix}r\cos(\Phi )\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})\\r\sin(\Phi )\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})\\r\sin(\Theta _{1})\cos(\Theta _{2})\cdots \cos(\Theta _{d-2})\\\vdots \\r\sin(\Theta _{d-3})\cos(\Theta _{d-2})\\r\sin(\Theta _{d-2})\\\end{pmatrix}}$

是一個微分同胚。 的雅可比矩陣的行列式，$\Psi$, $\det J_{\Psi }$, 由下式給出

$\det J_{\Psi }(r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})=r^{d-1}\cos(\Theta _{1})\cos(\Theta _{2})^{2}\cdots \cos(\Theta _{d-2})^{d-2}$

證明:

定理 6.8:

半徑為 $R\in \mathbb {R} _{>0}$ 的 $d$ 維球體的體積，$B_{R}(0)$ 由下式給出

$V_{d}(R):={\frac {\pi ^{d/2}}{\Gamma (d/2+1)}}R^{d}$

證明:

定理 6.9:

半徑為 $R\in \mathbb {R} _{>0}$ 的 $d$ 維球體的表面積（即 $\partial B_{R}(0)$ 的面積）由下式給出

$A_{d}(R):={\frac {d\pi ^{d/2}}{\Gamma (d/2+1)}}R^{d-1}$

半徑為 $R\in \mathbb {R} _{>0}$ 的 $d$ 維球體的表面積和體積之間存在“微分關係”（見練習 3）。

證明:

${\begin{aligned}A_{d}(R)&:={\frac {d\pi ^{d/2}}{\Gamma (d/2+1)}}R^{d-1}&\\&={\frac {d}{R}}V_{d}(R)&\\&={\frac {d}{R}}\int _{B_{R}(0)}1dx&{\text{ theorem 6.8}}\\&=\int _{B_{R}(0)}{\frac {1}{R}}\nabla \cdot xdx&\\&=\int _{\partial B_{R}(0)}{\frac {1}{R}}{\frac {x}{R}}\cdot xdx&{\text{ divergence theorem}}\\&=\int _{\partial B_{R}(0)}1dx&\end{aligned}}$$\Box$

格林函式

我們回顧積分論中的一個事實

引理 6.11: $f$ 可積 $\Leftrightarrow$ $|f|$ 可積。

我們省略證明。

定理 6.12:

由下式給出的函式 $P:\mathbb {R} ^{d}\to \mathbb {R}$，

$P(x):={\begin{cases}-{\frac {1}{2}}|x|&d=1\\-{\frac {1}{2\pi }}\ln(\|x\|)&d=2\\{\frac {1}{(d-2)A_{d}(1)\|x\|^{d-2}}}&d\geq 3\end{cases}}$

是泊松方程的格林函式。

我們只證明了定理 $d\geq 2$ 的情況。對於 $d=1$，請參考練習 4。

證明:

1.

我們證明 $P$ 在區域性可積。令 $K\subseteq \mathbb {R} ^{d}$ 為緊集。我們需要證明

$\int _{K}P(x)dx$

是一個實數，根據引理 6.11，這等價於

$\int _{K}|P(x)|dx$

是一個實數。在 $\mathbb {R} ^{d}$ 中，緊緻等價於有界且閉合，因此我們可以選擇一個 $R>0$，使得 $K\subset B_{R}(0)$。不失一般性，我們可以選擇 $R>1$，因為如果發現選擇的 $R$ 是 $\leq 1$，那麼任何 $R>1$ 也都可以。然後我們有

$\int _{K}|P(x)|dx\leq \int _{B_{R}(0)}|P(x)|dx$

對於 $d=2$，${\begin{aligned}\int _{B_{R}(0)}|P(x)|dx&=\int _{B_{1}(0)}-{\frac {1}{2\pi }}\ln(\|x\|)dx+\int _{B_{R}(0)\setminus B_{1}(0)}{\frac {1}{2\pi }}\ln(\|x\|)dx&\\&=\int _{B_{1}(0)}-{\frac {1}{2\pi }}\ln(\|x\|)dx+\int _{B_{R}(0)}{\frac {1}{2\pi }}\ln(\|x\|)dx-\int _{B_{1}(0)}{\frac {1}{2\pi }}\ln(\|x\|)dx&\\&=\int _{0}^{1}-{\frac {r}{\pi }}\ln(r)dr+\int _{0}^{R}{\frac {r}{2\pi }}\ln(r)dr&{\text{int. by subst. using spherical coords.}}\\&={\frac {1}{4\pi }}+{\frac {R^{2}}{4\pi }}\left(\ln(R)-{\frac {1}{2}}R\right)<\infty \end{aligned}}$

對於 $d\geq 3$，

${\begin{aligned}\int _{B_{R}(0)}|P(x)|dx&=\int _{B_{R}(0)}{\frac {1}{(d-2)A_{d}(1)\|x\|^{d-2}}}\\&=\int _{0}^{R}\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}\overbrace {|r^{d-1}\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})^{d-2}|} ^{\leq r^{d-1}}{\frac {1}{(d-2)A_{d}(1)r^{d-2}}}d\Theta _{1}\cdots d\Theta _{d-2}d\Phi dr\\&\leq \int _{0}^{R}2{\frac {r^{d-1}}{(d-2)A_{d}(1)r^{d-2}}}\pi ^{d-1}dr\\&={\frac {\pi ^{d-1}}{(d-2)A_{d}(1)}}R^{2}\end{aligned}}$

，其中我們將球座標替換積分法應用於第一行到第二行。

2.

我們計算了一些$P$ 的導數（見練習 5）

對於$d=2$，我們有

$\forall x\in \mathbb {R} ^{d}\setminus \{0\}:\nabla P(x)=-{\frac {x}{2\pi \|x\|^{2}}}$

對於$d\geq 3$，我們有

$\forall x\in \mathbb {R} ^{d}\setminus \{0\}:\nabla P(x)={\frac {x}{A_{d}(1)\|x\|^{d}}}$

對於所有 $d\geq 2$，我們有 $\forall x\in \mathbb {R} ^{d}\setminus \{0\}:\Delta P(x)=0$

3.

我們證明

$\forall x\in \mathbb {R} ^{d}:-\Delta {\mathcal {T}}_{P(\cdot -x)}=\delta _{x}$

令 $x\in \mathbb {R} ^{d}$ 和 $\varphi \in {\mathcal {D}}(\mathbb {R} ^{d})$ 是任意的。在證明的最後一步中，我們只處理 $-\Delta {\mathcal {T}}_{P(\cdot -x)}(\varphi )$ 項。由於 $\varphi \in {\mathcal {D}}(\mathbb {R} ^{d})$，$\varphi$ 的支撐是緊的。我們定義

$K:={\text{supp }}\varphi \cup {\overline {B_{1}(x)}}$

由於

${\begin{aligned}-\Delta {\mathcal {T}}_{P(\cdot -x)}(\varphi )&={\mathcal {T}}_{P(\cdot -x)}(-\Delta \varphi )&\\&=\int _{\mathbb {R} ^{d}}P(y-x)(-\Delta \varphi (y))dy&\\&=\int _{K}P(y-x)(-\Delta \varphi (y))dy&\\&=\lim _{\epsilon \downarrow 0}\int _{K}P(y-x)(-\Delta \varphi (y))\chi _{K\setminus B_{\epsilon }(x)}(y)dy&{\text{dominated convergence}}\\&=\lim _{\epsilon \downarrow 0}\int _{K\setminus B_{\epsilon }(x)}P(y-x)(-\Delta \varphi (y))dy&\\\end{aligned}}$

, 其中 $\chi _{K\setminus B_{\epsilon }(0)}$ 是 $K\setminus B_{\epsilon }(0)$ 的特徵函式。

最後一個積分是在 $K\setminus B_{\epsilon }(x)$ 上進行的（它是封閉集 $K$ 和 $\mathbb {R} ^{d}\setminus B_{\epsilon }(x)$ 的交集，因此也是有界的和緊緻的）。在這個區域中，根據本證明的第二部分，$P(y-x)$ 是連續可微的。因此，我們可以用分部積分法。注意到 ${\frac {x-y}{\|y-x\|}}$ 是 $y\in \partial B_{\epsilon }(x)$ 在 $K\setminus B_{\epsilon }(x)$ 上的外法線向量，我們得到

$\int _{K\setminus B_{\epsilon }(x)}P(y-x)\overbrace {(-\Delta \varphi (y))} {=-\nabla \cdot \nabla \varphi (y)}dy=\int _{\partial B_{\epsilon }(x)}P(y-x)\nabla \varphi (y)\cdot {\frac {x-y}{\|y-x\|}}dy-\int _{\mathbb {R} ^{d}\setminus B_{\epsilon }(x)}\nabla \varphi (y)\cdot \nabla P(y-x)dy$

進一步選擇 $w(x)={\tilde {G}}(x-\xi )\nabla \varphi (x)$。然後

$\nabla \cdot w(x)=\Delta \varphi (x){\tilde {G}}(x-\xi )+\langle \nabla {\tilde {G}}(x-\xi ),\nabla \varphi (x)\rangle$.

從高斯定理，我們得到

$\int _{\mathbb {R} ^{d}\setminus B_{R}(\xi )}\Delta \varphi (x){\tilde {G}}(x-\xi )+\langle \nabla {\tilde {G}}(x-\xi ),\nabla \varphi (x)\rangle dx=-\int _{\partial B_{R}(\xi )}\langle {\tilde {G}}(x-\xi )\nabla \varphi (x),{\frac {x-\xi }{\|x-\xi \|}}\rangle dx$

，其中右側的減號是因為我們需要 *向內* 法向量。由此立即得出

$\int _{\mathbb {R} ^{d}\setminus B_{R}(\xi )}-\Delta \varphi (x){\tilde {G}}(x-\xi )=\underbrace {\int _{\partial B_{R}(\xi )}\langle {\tilde {G}}(x-\xi )\nabla \varphi (x),{\frac {x-\xi }{\|x-\xi \|}}\rangle dx} _{:=J_{1}(R)}-\underbrace {\int _{\mathbb {R} ^{d}\setminus B_{R}(\xi )}\langle \nabla {\tilde {G}}(x-\xi ),\nabla \varphi (x)\rangle dx} _{:=J_{2}(R)}$

我們現在可以使用柯西-施瓦茨不等式計算以下內容

$|J_{1}(R)|\leq \int _{\partial B_{R}(\xi )}\|{\tilde {G}}(x-\xi )\nabla \varphi (x)\|\overbrace {\|{\frac {x-\xi }{\|x-\xi \|}}\|} ^{=1}dx$

$={\begin{cases}\displaystyle \int _{\partial B_{R}(\xi )}-{\frac {1}{2\pi }}\ln |x-\xi |\|\nabla \varphi (x)\|dx=\int _{\partial B_{1}(\xi )}-R{\frac {1}{2\pi }}\ln \|R(x-\xi )\|\|\nabla \varphi (Rx)\|dx&d=2\\\displaystyle \int _{\partial B_{R}(\xi )}{\frac {1}{(d-2)c}}{\frac {1}{|x-\xi |^{d-2}}}\|\nabla \varphi (x)\|dx=\int _{\partial B_{1}(\xi )}R^{d-1}{\frac {1}{(d-2)c}}{\frac {1}{|R(x-\xi )|^{d-2}}}&d\geq 3\end{cases}}$

$\leq {\begin{cases}\displaystyle \max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|\int _{\partial B_{1}(\xi )}-R{\frac {1}{2\pi }}\ln R^{2}dx=-\max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|{\frac {c}{2\pi }}R\ln R^{2}\to 0,R\to 0&d=2\\\displaystyle \max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|\int _{\partial B_{1}(\xi )}{\frac {1}{(d-2)c}}Rdx=\max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|{\frac {R}{d-2}}\to 0,R\to 0&d\geq 3\end{cases}}$

現在我們定義 $v(x)=\varphi (x)\nabla {\tilde {G}}(x-\xi )$，這將得到

$\nabla \cdot v(x)=\varphi (x)\underbrace {\Delta {\tilde {G}}(x-\xi )} _{=0,x\neq \xi }+\langle \nabla \varphi (x),\nabla {\tilde {G}}(x-\xi )\rangle$

對 $v$ 應用高斯定理，得到

$J_{2}(R)=\int _{\partial B_{R}(\xi )}\varphi (x)\langle \nabla {\tilde {G}}(x-\xi ),{\frac {x-\xi }{\|x-\xi \|}}\rangle dx$

$=\int _{\partial B_{R}(\xi )}\varphi (x)\langle -{\frac {x-\xi }{c\|x-\xi \|^{d}}},{\frac {x-\xi }{\|x-\xi \|}}\rangle dx=-{\frac {1}{c}}\int _{\partial B_{R}(\xi )}{\frac {1}{R^{d-1}}}\varphi (x)dx$

，注意到 $d=2\Rightarrow c=2\pi$.

我們還注意到

$\varphi (\xi )={\frac {1}{c}}\int _{\partial B_{1}(\xi )}\varphi (\xi )dx={\frac {1}{c}}\int _{\partial B_{R}(\xi )}{\frac {1}{R^{d-1}}}\varphi (\xi )dx$

因此，我們有

$\lim _{R\to 0}|-J_{2}(R)-\varphi (\xi )|\leq {\frac {1}{c}}\lim _{R\to 0}\int _{\partial B_{R}(\xi )}{\frac {1}{R^{d-1}}}|\varphi (\xi )-\varphi (x)|dx\leq \lim _{R\to 0}{\frac {1}{c}}\max _{x\in B_{R}(\xi )}|\varphi (x)-\varphi (\xi )|\int _{\partial B_{1}(\xi )}1dx$

$=\lim _{R\to 0}\max _{x\in B_{R}(\xi )}|\varphi (x)-\varphi (\xi )|=0$

由於 $\varphi$ 的連續性。

因此，我們可以得出結論：

$\forall \Omega {\text{ domain of }}\mathbb {R} ^{d}:\forall \varphi \in {\mathcal {D}}(\Omega ):-\Delta T_{{\tilde {G}}(\cdot -\xi )}(\varphi )=\lim _{R\to 0}J_{0}(R)=\lim _{R\to 0}J_{1}(R)-J_{2}(R)=0+\varphi (\xi )=\delta _{\xi }(\varphi )$.

因此， ${\tilde {G}}$ 是 $d\geq 2$ 的泊松方程的格林函式。

證畢。

球面積分

定理 6.12:

設 $f:\mathbb {R} ^{d}\to \mathbb {R}$ 為一個函式。 $\int _{\partial B_{R}(0)}f(x)dx=R^{d-1}\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}f\left(\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})\right)\cos(\Theta _{1})\cos(\Theta _{2})^{2}\cdots \cos(\Theta _{d-2})^{d-2}d\Theta _{1}d\Theta _{2}\cdots d\Theta _{d-2}d\Phi$

證明：我們選擇球面的邊界方向作為方向。我們知道對於 $\partial B_{r}(0)$，一個外向法向量場由 $\nu (x)={\frac {x}{r}}$給出。作為 $B_{r}(0)$ 的引數化，我們只選擇恆等函式，得到切空間的基是標準基，這反過來意味著 $B_{r}(0)$ 的體積形式為

$\omega _{B_{r}(0)}(x)=e_{1}^{*}\wedge \cdots \wedge e_{d}^{*}$

現在，我們使用法向量場來獲得 $\partial B_{r}(0)$ 的體積形式

$\omega _{\partial B_{r}(0)}(x)(v_{1},\ldots ,v_{d-1})=\omega _{B_{r}(0)}(x)(\nu (x),v_{1},\ldots ,v_{d-1})$

我們將 $\omega _{B_{r}(0)}(x)$ 的公式代入，然後使用拉普拉斯行列式公式

$=e_{1}^{*}\wedge \cdots \wedge e_{d}^{*}(\nu (x),v_{1},\ldots ,v_{d-1})={\frac {1}{r}}\sum _{i=1}^{d}(-1)^{i+1}x_{i}e_{1}^{*}\cdots \wedge e_{i-1}^{*}\wedge e_{i+1}^{*}\wedge \cdots \wedge e_{d}^{*}(v_{1},\ldots ,v_{d-1})$

作為 $\partial B_{r}(x)$ 的引數化，我們選擇半徑為 $r$ 的球座標。

我們計算球座標的雅可比矩陣

$J=\left({\begin{smallmatrix}\cos(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&r-\sin(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&-r\cos(\varphi )\sin(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&\cdots &\cdots &-r\cos(\varphi )\cos(\vartheta _{1})\cdots \sin(\vartheta _{d-2})\\\sin(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&r\cos(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&-r\sin(\varphi )\sin(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&\cdots &\cdots &-r\sin(\varphi )\cos(\vartheta _{1})\cdots \sin(\vartheta _{d-2})\\\vdots &0&\ddots &\ddots &\ddots &\vdots \\\vdots &\vdots &\ddots &\ddots &\ddots &\\\sin(\vartheta _{d-3})\cos(\vartheta _{d-2})&0&\cdots &0&r\cos(\vartheta _{d-3})\cos(\vartheta _{d-2})&r\sin(\vartheta _{d-3})\cos(\vartheta _{d-2})\\\sin(\vartheta _{d-2})&0&\cdots &\cdots &0&r\cos(\vartheta _{d-2})\end{smallmatrix}}\right)$

我們觀察到，在第一列中，我們只有球座標除以 $r$。如果我們固定 $r$，則第一列消失。我們稱得到的矩陣為 $J'$，我們的引數化，即球座標，其中 $r$ 為常數，記為 $\Psi$。然後我們有

$\Psi ^{*}\omega _{\partial B_{r}(0)}(x)(v_{1},\ldots ,v_{d-1})=\omega _{\partial B_{r}(0)}(\Psi (x))(J'v_{1},\ldots ,J'v_{d-1})$

$={\frac {1}{r}}\sum _{i=1}^{d}(-1)^{i+1}\Psi (x)_{i}e_{1}^{*}\cdots \wedge e_{i-1}^{*}\wedge e_{i+1}^{*}\wedge \cdots \wedge e_{d}^{*}(J'v_{1},\ldots ,J'v_{d-1})$

$={\frac {1}{r}}\sum _{i=1}^{d}(-1)^{i+1}\Psi (x)_{i}\det(e_{j}^{*}(J'v_{k}))_{j\neq i}=\det J\cdot \det(v_{1},\ldots ,v_{d-1})$

回顧

$\det J=r^{d-1}\cos(\phi _{1})^{n-2}\cos(\phi _{2})^{d-3}\cdots \cos(\phi _{d-2})$

, 由表面積分的定義可知結論成立。

定理 6.13:

令 $f:\mathbb {R} ^{d}\to \mathbb {R}$ 為一個函式。那麼

$\int _{\mathbb {R} ^{d}}f(x)dx=\int _{0}^{\infty }r^{d-1}\int _{\partial B_{1}(0)}f(rx)dxdr$

證明:

我們有 $r\Psi (1,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})=\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})$，其中 $\Psi$ 是球座標。因此，利用換元積分法、Fubini 定理以及上面單位球面積分公式，可得

${\begin{aligned}\int _{\mathbb {R} ^{d}}f(x)dx&=\int _{(0,\infty )\times (0,2\pi )\times (-\pi /2,\pi /2)^{d-2}}f(\Psi (x))|\det J_{\Psi }(x)|dx\\&=\int _{0}^{\infty }\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}f(\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2}))r^{d-1}\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})^{d-2}d\Theta _{1}\cdots d\Theta _{d-2}d\Phi dr\\&=\int _{0}^{\infty }r^{d-1}\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}f(r\Psi (1,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2}))\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})^{d-2}d\Theta _{1}\cdots d\Theta _{d-2}d\Phi dr\\&=\int _{0}^{\infty }r^{d-1}\int _{\partial B_{1}(0)}f(rx)dr\end{aligned}}$$\Box$

調和函式

定義 6.14：設 $O\subseteq \mathbb {R} ^{d}$ 為開集，設 $u:O\to \mathbb {R}$ 為一個函式。如果 $u\in {\mathcal {C}}^{2}(O)$ 且

$\forall x\in O:\Delta u(x)=0$

$u$ 被稱為**調和函式**。

定理 6.15:

設 $O\subseteq \mathbb {R} ^{d}$ 為開集，設 $u\in {\mathcal {C}}^{2}(O)$。以下條件等價

• $u$ 是調和的
• $\forall x\in O:\forall R{\text{ such that }}{\overline {B_{R}(0)}}\subset O:u(x)={\frac {1}{A_{d}(R)}}\int _{\partial B_{R}(x)}u(y)dy$
• $\forall x\in O:\forall R{\text{ such that }}{\overline {B_{R}(0)}}\subset O:u(x)={\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}u(y)dy$

證明：我們定義以下函式

$\phi (r)={\frac {1}{r^{d-1}}}\int _{\partial B_{r}(x)}u(y)dy$

首先，透過微分同胚 $y\mapsto x+y$ 進行座標變換，然後兩次應用單位球面上的積分公式，我們得到

$\phi (r)={\frac {1}{r^{d-1}}}\int _{\partial B_{r}(0)}u(y+x)dy=\int _{\partial B_{1}(0)}u(x+ry)dy$

首先，對被積函式求導，然後使用高斯定理，我們知道

$\phi '(r)=\int _{\partial B_{1}(0)}\langle \nabla u(x+ry),y\rangle dy=\int _{B_{1}(0)}\Delta u(x+ry)dy=0$

情況 1： 如果 $u$ 是調和的，那麼我們有

$\int _{B_{1}(0)}\Delta u(x+ry)dy=0$

，這就是 $\phi$ 為常數的原因。現在我們可以使用支配收斂定理進行以下計算

$\lim _{r\to 0}\phi (r)=\int _{\partial B_{1}(0)}\lim _{r\to 0}u(x+ry)dy=c(1)u(x)$

因此 $\phi (r)=c(1)u(x)$ 對於所有 $r$ 成立。

有了關係

$r^{d-1}c(1)=c(r)$

，這是因為我們對 $c(x),x\in \mathbb {R} _{>0}$ 的公式得出的，我們得到

$u(x)={\frac {\phi (r)}{c(1)}}={\frac {1}{c(1)}}{\frac {1}{r^{d-1}}}\int _{\partial B_{r}(x)}u(y)dy={\frac {1}{c(r)}}\int _{\partial B_{r}(x)}u(y)dy$

，這證明了第一個公式。

此外，我們可以透過首先進行變數變換，然後透過洋蔥皮積分，然後使用該定理的第一個公式，最後再透過洋蔥皮積分來證明第二個公式

$\int _{B_{r}(x)}u(y)dy=\int _{B_{r}(0)}u(y+x)dy=\int _{0}^{r}s^{d-1}\int _{\partial B_{1}(0)}u(y+sx)dxds=\int _{0}^{r}s^{d-1}u(x)\int _{\partial B_{1}(0)}1dxds=u(x)d(r)$

這表明如果 $u$ 是調和的，那麼計算 $u$ 的兩個公式都成立。

情況 2：假設 $u$ 不是調和函式。那麼存在一個 $x\in \Omega$ 使得 $-\Delta u(x)\neq 0$。不失一般性，我們假設 $-\Delta u(x)>0$；對於 $-\Delta u(x)<0$ 的證明將完全類似，只是不等式的方向會互換。那麼，由於如上所述，根據支配收斂定理，我們有

$\lim _{r\to 0}\phi '(r)=\int _{B_{1}(0)}\lim _{r\to 0}\Delta u(x+ry)dy>0$

由於 $\phi '$ 是連續的（根據支配收斂定理），因此 $\phi$ 在 $0$ 處增長，這與第一個公式矛盾。

與第二個公式的矛盾可以透過觀察到 $\phi '$ 是連續的，因此存在一個 $\sigma \in \mathbb {R} _{>0}$

$\forall r\in [0,\sigma ):\phi '(r)>0$

這意味著，由於

$\lim _{r\to 0}\phi (r)=\int _{\partial B_{1}(0)}\lim _{r\to 0}u(x+ry)dy=c(1)u(x)$

因此

$\phi (0)=c(1)u(x)$

, 那麼

$\forall r\in (0,\sigma ):\phi (r)>c(1)u(x)$

因此，透過與上面相同的計算，

$\int _{B_{r}(x)}u(y)dy=\int _{B_{r}(0)}u(y+x)dy=\int _{0}^{r}s^{d-1}\int _{\partial B_{1}(0)}u(y+sx)dxds>\int _{0}^{r}s^{d-1}u(x)\int _{\partial B_{1}(0)}1dxds=u(x)d(r)$

這表明（透過反證法證明）如果兩個公式之一成立，則$u\in C^{2}(\Omega )$ 是調和的。

定義 6.16:

域 是 $\mathbb {R} ^{d}$ 的一個開連通子集。

為了證明下一個定理，我們需要來自其他學科的兩個定理，第一個來自積分理論，第二個來自拓撲。

定理 6.17:

令 $B\subseteq \mathbb {R} ^{d}$ 且令 $f:B\to \mathbb {R}$ 是一個函式。如果

$\int _{B}|f(x)|dx=0$

則對於幾乎所有 $x\in B$ 有 $f(x)=0$。

定理 6.18:

在一個連通拓撲空間中，唯一既開又閉的集合是整個空間和空集。

我們將省略證明。

定理 6.19:

令 $\Omega \subseteq \mathbb {R} ^{d}$ 是一個域，令 $u:\Omega \to \mathbb {R}$ 是調和的。如果存在一個 $x\in \Omega$ 使得

$u(x)=\sup _{y\in \Omega }u(y)$

, 則 $u$ 是常數。

證明:

我們選擇

$B:=\left\{x\in \Omega :u(x)=\sup _{y\in \Omega }u(y)\right\}$

由於假設 $\Omega$ 是開集且 $B\subseteq \Omega$，對於每個 $x\in B$ 都存在一個 $R\in \mathbb {R} _{>0}$ 使得

${\overline {B_{R}(x)}}\subseteq \Omega$

根據定理 6.15，我們得到在這種情況下

$\sup _{y\in \Omega }u(y)=u(x)={\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}u(z)dz$

此外，

$\sup _{y\in \Omega }u(y)=\sup _{y\in \Omega }u(y){\frac {V_{d}(R)}{V_{d}(R)}}={\frac {1}{V_{d}(R)}}\int _{B_{r}(x)}\sup _{y\in \Omega }u(y)dz$

，這就是為什麼

${\begin{aligned}{\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}u(z)dz=\int _{B_{R}(x)}\sup _{y\in \Omega }u(y)dz\\\Leftrightarrow {\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}(u(z)-\sup _{y\in \Omega }u(y))dz=0\end{aligned}}$

由於

$\forall z\in \Omega :\sup _{y\in \Omega }u(y)\geq u(z)$

，我們甚至有

$0={\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}(u(z)-\sup _{y\in \Omega }u(y))dz=-{\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}|u(z)-\sup _{y\in \Omega }u(y)|dz$

根據定理 6.17，我們得出結論

$u(z)=\sup _{y\in \Omega }u(y)$

在 $B_{R}(x)$ 中幾乎處處成立，並且由於

$z\mapsto u(z)-\sup _{y\in \Omega }u(y)$

是連續的，即使

$u(z)=\sup _{y\in \Omega }u(y)$

在 $B_{R}(x)$ 中處處成立（參見練習 6）。因此，$B_{R}(0)\subseteq B$，並且由於 $x\in B$ 是任意的，$B$ 是開集。

此外，

$B=u^{-1}\left(\left\{\sup _{y\in \Omega }u(y)\right\}\right)$

並且 $u$ 是連續的。因此，由於單點集是閉集，引理 3.13 指出 $B$ 在 $\Omega$ 中是閉集。因此 $B$ 既是開集又是閉集。根據定理 6.18，我們得到 $B=\emptyset$ 或 $B=\Omega$。由於假設 $B$ 非空，我們有 $B=\Omega$。$\Box$

定理 6.18:

令 $\Omega \subseteq \mathbb {R} ^{d}$ 是一個域，令 $u:\Omega \to \mathbb {R}$ 是調和的。如果存在一個 $x\in \Omega$ 使得

$u(x)=\inf _{y\in \Omega }u(y)$

, 則 $u$ 是常數。

證明：參見練習 7。

推論 6.20:

令 $\Omega \subseteq \mathbb {R} ^{d}$ 是一個有界區域，並令 $u:{\overline {\Omega }}\to \mathbb {R}$ 在 $\Omega$ 上是調和的，並且在 ${\overline {\Omega }}$ 上是連續的。那麼

$\forall x\in {\overline {\Omega }}:\inf _{y\in \partial \Omega }u(y)\leq u(x)\leq \sup _{y\in \partial \Omega }u(y)$

證明:

定理 6.20:

令 $O\subseteq \mathbb {R} ^{d}$ 是一個開集，並且 $u:O\to \mathbb {R}$ 是一個調和函式，令 $x_{0}\in O$ 並且令 $R>0$ 使得 ${\overline {B_{R}(x_{0})}}\subset O$。那麼

$\forall x\in B_{R}(x_{0}):u(x)={\frac {R^{2}+\|x-x_{0}\|^{2}}{RA_{d}(1)}}\int _{\partial B_{R}(x_{0})}{\frac {u(y)}{\|x-y\|^{d}}}dy$

證明:

接下來我們將證明每個調和函式 $u\in {\mathcal {C}}^{2}(O)$ 事實上自動包含在 ${\mathcal {C}}^{\infty }(O)$ 中。

定理 6.25：設 $O\subseteq \mathbb {R} ^{d}$ 是開集，並設 $u:O\to \mathbb {R}$ 是調和函式。則 $u\in {\mathcal {C}}^{\infty }(O)$。此外，對於所有 $n\in \mathbb {N}$，存在一個常數 $C_{d,n}$ 僅取決於維度 $d$ 和 $n$，使得對於所有 $x_{0}\in O$ 和 $R>0$ 使得 $B_{R}(x_{0})\subseteq O$

$\forall \alpha \in \mathbb {N} ^{d}{\text{ with }}|\alpha |=n:\partial _{\alpha }u(x)\leq {\frac {C_{d,n}}{R^{d+n}}}\int _{B_{R}(x_{0})}|u(y)|dy$

證明:

定義 6.26:

設 $(u_{l})_{l\in \mathbb {N} }$ 是調和函式序列，並設 $u:O\to \mathbb {R}$ 是一個函式。 $(u_{l})_{l\in \mathbb {N} }$ 區域性一致收斂到 $u$ 當且僅當

定理 6.27:

設 $O\subseteq \mathbb {R} ^{d}$ 為開集，設 $u_{l}:O\to \mathbb {R} ,l\in \mathbb {N}$ 為調和函式，使得序列 $(u_{l})_{l\in \mathbb {N} }$ 區域性一致收斂於函式 $u:O\to \mathbb {R}$。那麼 $u$ 也是調和的。

證明:

定義 6.28:

定理 6.29: (阿澤拉-阿斯科利) 設 $F$ 是定義在緊集 $K$ 上的一組連續函式。那麼以下兩個命題等價

1. ${\overline {F}}$（$F$ 的閉包）是緊的
2. $F$ 是有界且等度連續的

證明:

定義 6.30:

定理 6.31:

設 $(u_{l})_{l\in \mathbb {N} }$ 是區域性一致有界調和函式序列。那麼它有一個區域性一致收斂的子序列。

證明:

邊界值問題

泊松方程的狄利克雷問題是尋找以下方程的解：

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

解的唯一性

如果 $\Omega$ 是有界的，那麼我們可以知道，如果問題

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

有一個解 $u_{1}$，那麼這個解在 $\Omega$ 上是唯一的。

證明：令 $u_{2}$ 為另一個解。如果我們定義 $u=u_{1}-u_{2}$，那麼 $u$ 顯然滿足問題

${\begin{cases}-\Delta u(x)=0&,x\in \Omega \\u(x)=0&x\in \partial \Omega \end{cases}}$

，因為 $-\Delta (u_{1}(x)-u_{2}(x))=-\Delta u_{1}(x)-(-\Delta u_{2}(x))=f(x)-f(x)=0$ 對於 $x\in \Omega$，並且 $u_{1}(x)-u_{2}(x)=g(x)-g(x)=0$ 對於 $x\in \partial \Omega$。

根據以上最小值和最大值原理的推論，我們得到 $u$ 不僅在邊界上恆為零，在整個域 $\Omega$ 上也是恆為零。因此 $u_{1}(x)-u_{2}(x)=0\Leftrightarrow u_{1}(x)=u_{2}(x)$ 在 $\Omega$ 上。這就是我們要證明的結論。

第一類格林函式

令 $\Omega \subseteq \mathbb {R} ^{d}$ 為一個域。令 ${\tilde {G}}$ 為泊松方程的格林核，我們已經在上文中計算了它，即

${\tilde {G}}(x):={\begin{cases}-{\frac {1}{2}}|x|&d=1\\-{\frac {1}{2\pi }}\ln \|x\|&d=2\\{\frac {1}{(d-2)c}}{\frac {1}{\|x\|^{d-2}}}&d\geq 3\end{cases}}$

, 其中 $c:=\int _{\partial B_{1}(0)}1dz$ 表示 $B_{1}(0)\subset \mathbb {R} ^{d}$ 的表面積。

假設存在一個函式 $h:\Omega \times \Omega \to \mathbb {R}$ 滿足以下條件

${\begin{cases}-\Delta h(x,\xi )=0&x\in \Omega \\h(x,\xi )={\tilde {G}}(x-\xi )&x\in \partial \Omega \end{cases}}$

那麼，$-\Delta$ 對 $\Omega$ 的**第一類格林函式**定義如下

${\tilde {G}}_{\Omega }(x,\xi ):={\tilde {G}}(x-\xi )-h(x,\xi )$

${\tilde {G}}(x-\xi )-h(x,\xi )$ 自然地成為了 $-\Delta$ 的格林函式。這可以透過與驗證 ${\tilde {G}}$ 是格林核完全相同的方式進行驗證。我們只需要知道 $h$ 在極限過程中沒有作用，因為它是有界的。

這個函式的一個性質是它滿足以下條件

${\begin{cases}-\Delta {\tilde {G}}_{\Omega }(x,\xi )=0&x\in \Omega \setminus \{\xi \}\\{\tilde {G}}_{\Omega }(x,\xi )=0&x\in \partial \Omega \end{cases}}$

這兩個方程中的第二個方程從定義中可以明顯看出，而第一個方程則可以從我們上面計算（在計算格林函式時）得到的結果推匯出，即對於$x\neq 0$，有$\Delta {\tilde {G}}(x)=0$。

表示公式

設$\Omega \subseteq \mathbb {R} ^{d}$ 是一個區域，設$u\in C^{2}(\Omega )$ 是狄利克雷問題的解

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

。那麼$u$ 具有以下表示公式

$u(\xi )=\int _{\Omega }-\Delta u(y){\tilde {G}}_{\Omega }(y,\xi )dy-\int _{\partial \Omega }u(y)\nu (y)\nabla _{y}{\tilde {G}}_{\Omega }(y,\xi )dy$

，其中${\tilde {G}}_{\Omega }$ 是$\Omega$ 的第一類格林函式。

證明：令

$J(\epsilon ):=\int _{\Omega \setminus B_{\epsilon }(\xi )}-\Delta u(y){\tilde {G}}_{\Omega }(y,\xi )dy$

。根據支配收斂定理，我們有

$\lim _{\epsilon \to 0}J(\epsilon )=\int _{\Omega }-\Delta u(y){\tilde {G}}_{\Omega }(y,\xi )dy$

使用多維積分分部，可以得到

$J(\epsilon )=-\int _{\partial \Omega }\underbrace {{\tilde {G}}_{\Omega }(y,\xi )} _{=0}\langle \nabla u(y),\nu (y)\rangle dy+\int _{\partial B_{\epsilon }(\xi )}{\tilde {G}}_{\Omega }(y,\xi )\langle \nabla u(y),{\frac {y-\xi }{\|y-\xi \|}}\rangle dy+\int _{\Omega \setminus B_{\epsilon }(\xi )}\langle \nabla u(y),\nabla _{x}{\tilde {G}}_{\Omega }(y,\xi )\rangle dy$

$=\underbrace {\int _{\partial B_{\epsilon }(\xi )}{\tilde {G}}_{\Omega }(y,\xi )\langle \nabla u(y),{\frac {y-\xi }{\|y-\xi \|}}\rangle dy} _{:=J_{1}(\epsilon )}-\int _{\Omega \setminus B_{\epsilon }(\xi )}\Delta {\tilde {G}}_{\Omega }(y,\xi )u(y)dy$

$-\underbrace {\int _{\partial B_{\epsilon }(\xi )}u(y)\langle \nabla {\tilde {G}}_{\Omega }(y,\xi ),{\frac {y-\xi }{\|y-\xi \|}}\rangle dy} _{:=J_{2}(\epsilon )}-\int _{\partial \Omega }u(y)\langle \nabla {\tilde {G}}_{\Omega }(y,\xi ),\nu (y)\rangle dy$

當我們證明泊松方程的格林函式公式時，我們已經證明了

$\lim _{\epsilon \to 0}-J_{2}(\epsilon )=u(\xi )$ 和

$\lim _{\epsilon \to 0}J_{1}(\epsilon )=0$

驗證這一點唯一需要的額外資訊是$h\in C^{\infty }(\Omega )$，這就是它保持有界的原因，而${\tilde {G}}$ 當$\epsilon \to 0$ 時趨於無窮大，這就是$h$ 在極限過程中不起作用的原因。

這證明了公式。

球體上的調和函式：狄利克雷問題的一個特例

球體的第一類格林函式

讓我們選擇

$h(x,\xi )={\tilde {G}}\left({\frac {\|\xi \|}{r}}\left(x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi \right)\right)$

那麼

${\tilde {G}}_{B_{r}(x_{0})}(x,\xi ):={\tilde {G}}(x-\xi )-h(x-x_{0},\xi -x_{0})$

是$B_{r}(x_{0})$ 的第一類格林函式。

證明：因為$\xi -x_{0}\in B_{r}(0)\Rightarrow {\frac {r^{2}}{\|\xi -x_{0}\|^{2}}}(\xi -x_{0})\notin B_{r}(0)$，因此

$\forall x,\xi \in B_{r}(0):-\Delta _{x}h(x-x_{0},\xi -x_{0})=0$

此外，我們得到

$\int _{B_{r}(x_{0})}-\Delta \varphi (x){\tilde {G}}_{\Omega }(x,\xi )dx=\int _{B_{r}(x_{0})}-\Delta \varphi (x){\tilde {G}}(x-\xi )dx+\int _{B_{r}(x_{0})}\varphi (x)-\Delta h(x,\xi )dx=\varphi (\xi )+0$

，這就是${\tilde {G}}_{\Omega }(x,\xi )$ 是格林函式的原因。

邊界的性質來自以下計算

$\forall x\in \partial B_{r}(0):\|x-\xi \|^{2}=\langle x-\xi ,x-\xi \rangle =r^{2}+\|\xi \|^{2}-2\langle x,\xi \rangle ={\frac {\|\xi \|^{2}}{r^{2}}}(\langle x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi ,x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi \rangle )={\frac {\|\xi \|^{2}}{r^{2}}}\|x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi \|^{2}$

因此，$x\in \partial B_{r}(0)\Rightarrow h(x,\xi )={\tilde {G}}(x,\xi )$，因為 ${\tilde {G}}$ 是徑向對稱的。

解的公式

讓我們考慮以下問題

${\begin{cases}-\Delta u(x)=0&x\in B_{r}(0)\\u(x)=\varphi (x)&x\in \partial B_{r}(0)\end{cases}}$

這裡 $\varphi$ 應該在 $\partial B_{r}(0)$ 上是連續的。 那麼以下結論成立：該問題的唯一解 $u\in C({\overline {B_{r}(0)}})\cap C^{2}(B_{r}(0))$ 由以下給出：

$u(\xi )={\begin{cases}\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,\xi )\rangle \varphi (y)dy&\xi \in B_{r}(0)\\\varphi (\xi )&\xi \in \partial B_{r}(0)\end{cases}}$

證明：唯一性我們已經證明了；我們已經證明了對於所有 $-\Delta$ 在有界域上的狄利克雷問題（單位球當然是有界的），解是唯一的。

因此，剩下的就是證明上述函式是問題的解。為此，我們首先注意到

$-\Delta \int _{\partial B_{r}(0)}\langle -\nu (y),{\tilde {\nabla }}_{y}G_{B_{r}(0)}(y,\xi )\rangle \varphi (y)dy=-\Delta \int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}({\tilde {G}}(y-\xi )-h(y,\xi ))\rangle \varphi (y)dy$

令 $0<s<r$ 為任意值。由於 ${\tilde {G}}_{B_{r}(0)}$ 在 $B_{s}(0)$ 上是連續的，我們有，在 $B_{s}(0)$ 上它是 有界的。因此，根據基本估計，我們知道積分是有界的，因為球面（積分的集合）是一個有界集合，因此整個積分必須始終低於某個常數。但這意味著，我們允許在 $B_{s}(0)$ 上對積分進行微分，由於 $r>s>0$ 是任意的，我們可以直接得出結論，在 $B_{r}(0)$ 上，

$-\Delta u(\xi )=\int _{\partial B_{r}(0)}\overbrace {-\Delta (\langle -\nu (y),{\tilde {\nabla }}_{y}{\tilde {G}}(x-\xi )-h(x,\xi )\rangle \varphi (y))} ^{=0}dy=0$

此外，我們必須證明 $\forall x\in \partial B_{r}(0):\lim _{y\to x}u(y)=\varphi (x)$，即 $u$ 在邊界上是連續的。

為此，我們首先注意到

$\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,\xi )\rangle dy=1$

這是因為，如果 $u\equiv 1$，那麼 $u$ 是以下問題的解

${\begin{cases}-\Delta u(x)=0&x\in B_{r}(0)\\u(x)=1&x\in \partial B_{r}(0)\end{cases}}$

並應用表示公式。

此外，如果 $\|x-x^{*}\|<{\frac {1}{2}}\delta$ 並且 $\|y-x^{*}\|\geq \delta$，根據三角不等式，我們有

$\|x-y\|\geq |\|y-x^{*}\|-\|x^{*}-x\||\geq {\frac {1}{2}}\delta$

此外，根據三角不等式，我們還可以得到

$(r^{2}-\|x\|^{2})=(r+\|x\|)(r-\|x\|)=(r+\|x\|)(\|x^{*}\|-\|x\|)\leq 2r\|x^{*}-x\|$

令 $\epsilon >0$ 為任意值，並令 $x^{*}\in \partial B_{r}(0)$。 然後，根據 $\varphi$ 的連續性，我們可以選擇 $\delta >0$ 使得

$\|x-x^{*}\|<\delta \Rightarrow |\varphi (x)-\varphi (x^{*})|<{\frac {\epsilon }{2}}$.

最後，藉助我們之前做出的所有估計，我們可以展示最後一個不等式鏈，證明表示公式是正確的。

$|u(x)-u(x^{*})|=|u(x)-1\cdot \varphi (x^{*})|=\left|\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle (\varphi (x)-\varphi (x^{*}))dy\right|$

$\leq {\frac {\epsilon }{2}}\int _{\partial B_{r}(0)\cap B_{\delta }(x^{*})}|\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle |dy+2\|\varphi \|_{\infty }\int _{\partial B_{r}(0)\setminus B_{\delta }(x^{*})}|\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle |dy$

$\leq {\frac {\epsilon }{2}}+2\|\varphi \|_{\infty }\int _{\partial B_{r}(0)\setminus B_{\delta }(x^{*})}{\frac {r^{2}-\|x\|^{2}}{rc(1)\left({\frac {\delta }{2}}\right)^{d}}}dy\leq {\frac {\epsilon }{2}}+2\|\varphi \|_{\infty }r^{d-2}{\frac {r^{2}-\|x\|^{2}}{\left({\frac {\delta }{2}}\right)^{d}}}$

由於 $x\to x^{*}$ 意味著 $r^{2}-\|x\|^{2}\to 0$，我們可以選擇 $x$ 足夠接近 $x^{*}$ 使得

$2\|\varphi \|_{\infty }r^{d-2}{\frac {r^{2}-\|x\|^{2}}{\left({\frac {\delta }{2}}\right)^{d}}}<{\frac {\epsilon }{2}}$。由於$\epsilon >0$是任意的，這完成了證明。

障礙

設$\Omega \subset \mathbb {R} ^{d}$是一個域。函式$b:\mathbb {R} ^{d}\to \mathbb {R}$被稱為關於$y\in \partial \Omega$的障礙 當且僅當滿足以下性質

1. $b$是連續的
2. $b$在$\Omega$上是超調和的
3. $b(y)=0$
4. $\forall x\in \mathbb {R} ^{d}\setminus \Omega :b(x)>0$

外球條件

令 $\Omega \subseteq \mathbb {R} ^{d}$ 為一個區域。當且僅當對於所有的 $x\in \partial \Omega$ 都存在一個球 $B_{r}(z)\subseteq \mathbb {R} ^{d}\setminus \Omega$ 使得 $x\in \partial B_{r}(z)$，其中 $z\in \mathbb {R} ^{d}\setminus \Omega$ 和 $r\in \mathbb {R} _{\geq 0}$，則稱它滿足外球條件。

次調和函式和超調和函式

令 $\Omega \subseteq \mathbb {R} ^{d}$ 為一個區域，且 $v\in C(\Omega )$。

我們稱 $v$ 為次調和函式，當且僅當

$v(x)\leq {\frac {1}{d(r)}}\int _{B_{r}(x)}v(y)dy$

我們稱 $v$ 為超調和函式，當且僅當

$v(x)\geq {\frac {1}{d(r)}}\int _{B_{r}(x)}v(y)dy$

從這個定義我們可以看出，一個函式是調和函式當且僅當它既是次調和函式又是超調和函式。

超調和函式的最小值原理

在 $\Omega$ 上的超調和函式 $u$ 在 $\Omega$ 的邊界 $\partial \Omega$ 上取得其最小值。

證明：與調和函式的最小值和最大值原理的證明幾乎相同。作為一個練習，你可以嘗試自己證明這個最小值原理。

調和降低

設 $u\in {\mathcal {S}}_{\varphi }(\Omega )$，設 $B_{r}(x_{0})\subset \Omega$。如果我們定義

${\tilde {u}}(x)={\begin{cases}u(x)&x\notin B_{r}(x_{0})\\\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle \varphi (y)dy&x\in B_{r}(x_{0})\end{cases}}$

，那麼 ${\tilde {u}}\in {\mathcal {S}}_{\varphi }(\Omega )$。

證明：在這個證明中，需要注意的是 ${\tilde {u}}$ 在 $B_{r}(x_{0})$ 內部的公式不過是球上狄利克雷問題的解公式。因此，我們立即得到 ${\tilde {u}}$ 是超調和的，而且，在 $\partial \Omega$ 上的值不會改變，這就是為什麼 ${\tilde {u}}\in {\mathcal {S}}_{\varphi }(\Omega )$。這正是要證明的。

定義 3.1

設 $\varphi \in C(\partial \Omega )$。然後我們定義以下集合

${\mathcal {S}}_{\varphi }(\Omega ):=\{u\in C({\overline {\Omega }}):u{\text{ superharmonic and }}x\in \partial \Omega \Rightarrow u(x)\geq \varphi (x)\}$

引理 3.2

${\mathcal {S}}_{\varphi }(\Omega )$ 不為空，並且

$\forall u\in {\mathcal {S}}_{\varphi }(\Omega ):\forall x\in \Omega :u(x)\geq \min _{y\in \partial \Omega }\varphi (y)$

證明：第一部分可以透過選擇常數函式 $u(x)=\max _{y\in \partial \Omega }\varphi (y)$ 得出，該函式是調和的，因此是超調和的。第二部分從超調和函式的最小值原理得出。

引理 3.3

令 $u_{1},u_{2}\in {\mathcal {S}}_{\varphi }(\Omega )$。如果我們現在定義 $u(x)=\min\{u_{1}(x),u_{2}(x)\}$，則 $u\in {\mathcal {S}}_{\varphi }(\Omega )$。

證明：邊界上的條件得到滿足，因為

$\forall x\in \partial \Omega :u_{1}(x)\geq \varphi (x)\wedge u_{2}(x)\geq \varphi (x)$

$u$ 是超調和的，因為，如果我們（不失一般性）假設 $u(x)=u_{1}(x)$，則可以得出

$u(x)=u_{1}(x)\geq {\frac {1}{d(r)}}\int _{B_{r}(x)}u_{1}(y)dy\geq {\frac {1}{d(r)}}\int _{B_{r}(x)}u(y)dy$

，由於積分的單調性。這個論點對所有 $x\in \Omega$ 都有效，因此 $u$ 是超調和的。

引理 3.4

如果 $\Omega \subset \mathbb {R} ^{d}$ 是有界的，並且 $\varphi \in C(\partial \Omega )$，則函式

$u(x)=\inf\{v(x)|v\in {\mathcal {S}}_{\varphi }(\Omega )\}$

是調和的。

證明:

引理 3.5

如果 $\Omega$ 滿足外球條件，則對於所有 $y\in \partial \Omega$ 都存在一個勢壘函式。

佩龍存在定理

設 $\Omega \subset \mathbb {R} ^{d}$ 是一個滿足外球條件的有界域。則泊松方程的狄利克雷問題，即再次寫為

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

有一個解 $u\in C^{\infty }(\Omega )\cap C({\overline {\Omega }})$。

證明:

讓我們總結一下本節的結果。

推論 6.last:

設 $\Omega \subset \mathbb {R} ^{d}$ 是一個滿足外球條件的域，設 $f\in {\mathcal {C}}^{2}(\mathbb {R} ^{d})$，設 $g:\partial \Omega \to \mathbb {R}$ 是連續的，並且設 $P_{\Omega }$ 是 $\Omega$ 的第一類格林函式。則

$u(x)=\int _{\Omega }f(y)P_{\Omega }(y,x)dy-\int _{\partial \Omega }g(y)\nu (y)\cdot \nabla _{y}P_{\Omega }(y,x)dy$

是邊值問題的唯一連續解

${\begin{cases}\forall x\in \Omega :&-\Delta u(x)=f(x)\\\forall x\in \partial \Omega :&u(x)=g(x)\end{cases}}$

在下一章中，我們將研究熱方程。

練習

1. 使用定理 6.2 證明定理 6.3（提示：在定理 6.2 中選擇 $\mathbf {V} (x)=\mathbf {W} (x)f(x)$）。
2. 證明 $\forall n\in \mathbb {N} :\Gamma (n+1)=n!$，其中 $n!$ 是 $n$ 的階乘。
3. 計算 $V_{d}'(R)$。你以前見過這個函式嗎？
4. 證明對於 $d=1$，在定理 6.11 中定義的函式 $P_{d}$ 是泊松方程的格林函式（提示：使用分部積分兩次）。
5. 對於所有 $d\geq 2$ 和 $x\in \mathbb {R} ^{d}\setminus \{0\}$，計算 $\nabla P_{d}(x)$ 和 $\Delta P_{d}(x)$。
6. 設 $O\subseteq \mathbb {R} ^{d}$ 為開集，且 $f:O\to \mathbb {R} ^{d}$ 為連續函式。證明 $f(x)=0$ 在 $O$ 中幾乎處處成立，則意味著 $f(x)=0$ 在 $O$ 中處處成立。
7. 透過對定理 6.19 的證明進行模仿，證明定理 6.20。
8. 對於所有維度$d\geq 2$，給出向量$\alpha ,\beta \in \mathbb {N} _{0}^{d}$ 的一個例子，使得既不滿足$\alpha \leq \beta$ 也不滿足$\beta \leq \alpha$。