在深入探討本章之前,讓我們先探討測試函式的概念。考慮兩個在區間  上分段常數,並在其他地方為零的兩個函式;例如,這兩個函式
上分段常數,並在其他地方為零的兩個函式;例如,這兩個函式

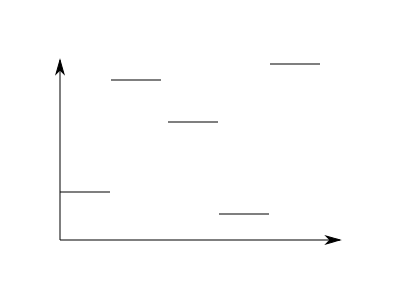
我們把左側的函式稱為  ,右側的函式稱為
,右側的函式稱為  。
。
當然,我們可以很容易地看出這兩個函式是不同的;它們在區間  上不同;但是,假設我們失明瞭,我們唯一能瞭解這兩個函式的方法是計算積分
上不同;但是,假設我們失明瞭,我們唯一能瞭解這兩個函式的方法是計算積分
 和
和 
對於給定函式集  中的函式
中的函式  。
。
我們繼續選擇  足夠聰明,使得對兩個積分的五次評估足以證明
足夠聰明,使得對兩個積分的五次評估足以證明  。為此,我們首先引入特徵函式。令
。為此,我們首先引入特徵函式。令  為任意集合。
為任意集合。 的特徵函式 定義為
的特徵函式 定義為

根據此定義,我們選擇函式集  為
為

很容易看出(見練習 1),對於  ,表示式
,表示式

等於  在區間
在區間  上的值,對於
上的值,對於  也是如此。但由於這兩個函式在區間
也是如此。但由於這兩個函式在區間  上的值唯一確定(因為它們在其他地方都為零),我們可以使用以下等式測試
上的值唯一確定(因為它們在其他地方都為零),我們可以使用以下等式測試

這顯然需要對每個積分進行五次計算,因為  .
.
由於我們使用  中的函式來測試
中的函式來測試  和
和  ,我們稱之為測試函式。我們現在要問的是,這個概念是否可以從像
,我們稱之為測試函式。我們現在要問的是,這個概念是否可以從像  和
和  這樣的函式(它們在某些區間上是分段常數,在其他地方為零)推廣到連續函式。下一章將證明這是真的。
這樣的函式(它們在某些區間上是分段常數,在其他地方為零)推廣到連續函式。下一章將證明這是真的。
為了更簡潔地寫下凸起函式的定義,我們需要以下兩個定義
現在我們可以簡要地定義 bump 函式
這兩個性質使得該函式看起來確實像一個 bump,如下例所示
 標準 mollifier
標準 mollifier  在維度
在維度 
示例 3.4: 標準平滑函式  ,定義如下:
,定義如下:

,其中  ,是一個凸函式(參見練習 2)。
,是一個凸函式(參見練習 2)。
為了簡明地寫出 Schwartz 函式的定義,我們需要先給出兩個有用的定義。
現在我們準備定義 Schwartz 函式。
定義 3.7:
我們稱  為 **Schwartz 函式** 當且僅當以下兩個條件滿足:
為 **Schwartz 函式** 當且僅當以下兩個條件滿足:


這裡, 代表函式
代表函式  .
.


例 3.8:函式

是一個 Schwartz 函式。
定理 3.9:
每個 bump 函式也是 Schwartz 函式。
這意味著例如標準 mollifier 是一個 Schwartz 函式。
證明:
令  為一個 bump 函式。那麼,根據 bump 函式的定義,
為一個 bump 函式。那麼,根據 bump 函式的定義, 。根據 bump 函式的定義,我們選擇
。根據 bump 函式的定義,我們選擇  使得
使得

, 在  中,一個集合是緊緻的當且僅當它是閉合且有界的。此外,對於任意
中,一個集合是緊緻的當且僅當它是閉合且有界的。此外,對於任意  ,
,


現在我們定義碰撞函式(Schwartz 函式)序列收斂到碰撞函式(Schwartz 函式)的含義。
定義 3.11:
我們說,Schwartz 函式序列  收斂到
收斂到  當且僅當滿足以下條件:
當且僅當滿足以下條件:

定理 3.12:
令  是一個任意 bump 函式序列。如果
是一個任意 bump 函式序列。如果  關於 bump 函式的收斂概念,那麼根據 Schwartz 函式的收斂概念,也有
關於 bump 函式的收斂概念,那麼根據 Schwartz 函式的收斂概念,也有  。
。
證明:
設 為開集,並設
為開集,並設 為
為 中的一個序列,使得
中的一個序列,使得 ,其中收斂概念是
,其中收斂概念是 的收斂概念。因此,設
的收斂概念。因此,設 為包含所有
為包含所有 的緊集。由此也得到
的緊集。由此也得到 ,因為否則
,因為否則 ,其中
,其中 是
是 在
在 外取的任何非零值;這將與我們收斂概念下的
外取的任何非零值;這將與我們收斂概念下的 矛盾。
矛盾。
在 中,“緊緻”等價於“有界且閉合”。因此,對於某個
中,“緊緻”等價於“有界且閉合”。因此,對於某個 ,有
,有 。因此,對於所有多重指標
。因此,對於所有多重指標

因此,該序列關於 Schwartz 函式收斂的概念收斂。
在本節中,我們想要展示,可以透過計算積分來測試連續函式 的相等性
的相等性
 和
和 
對於所有的  (因此,對所有
(因此,對所有  評估積分也將足夠,因為根據定理 3.9,
評估積分也將足夠,因為根據定理 3.9, )。
)。
但在我們能夠展示這一點之前,我們需要一個經過修改的平滑化函式,該函式的修改依賴於一個引數,以及關於該經過修改的平滑化函式的兩個引理。
定義 3.13:
對於  ,我們定義
,我們定義
 .
.
引理 3.14:
令  。然後
。然後
 .
.
證明:
從  的定義可以得出
的定義可以得出
 .
.
此外,對於 

因此,並且由於

,我們有


為了證明下一個引理,我們需要積分理論中的以下定理
定理 3.15: (多元積分換元法)
如果  是開集,並且
是開集,並且  是一個微分同胚,則
是一個微分同胚,則

我們將省略證明,因為理解它對於理解本維基百科並不重要。
引理 3.16:
令  。然後
。然後
 .
.
證明:
- 1 − ‖ x ‖ d x Def. of η = 1 {\displaystyle {\begin{aligned}\int _{\mathbb {R} ^{d}}\eta _{R}(x)dx&=\int _{\mathbb {R} ^{d}}\eta \left({\frac {x}{R}}\right){\big /}R^{d}dx&{\text{Def. of }}\eta _{R}\\&=\int _{\mathbb {R} ^{d}}\eta (x)dx&{\text{integration by substitution using }}x\mapsto Rx\\&=\int _{B_{1}(0)}\eta (x)dx&{\text{Def. of }}\eta \\&={\frac {\int _{B_{1}(0)}e^{-{\frac {1}{1-\|x\|}}}dx}{\int _{B_{1}(0)}e^{-{\frac {1}{1-\|x\|}}}dx}}&{\text{Def. of }}\eta \\&=1\end{aligned}}}


現在我們準備證明測試函式的“測試”性質
定理 3.17:
設  是連續的。如果
是連續的。如果
 ,
,
那麼  .
.
證明:
令  是任意的,並令
是任意的,並令  。由於
。由於  是連續的,存在一個
是連續的,存在一個  使得
使得

那麼我們有

因此, 。類似的推理也表明
。類似的推理也表明  。但根據假設,我們有
。但根據假設,我們有

由於實數中的極限是唯一的,因此可以得出  ,並且由於
,並且由於  是任意的,我們得到
是任意的,我們得到  。
。
備註 3.18:設  是連續的。如果
是連續的。如果
 ,
,
那麼  .
.
證明:
這源於所有凸起函式都是 Schwartz 函式,這就是為什麼定理 3.17 的要求得到滿足的原因。
設  且
且  在區間
在區間  上是常數。證明
上是常數。證明

- 證明在例 3.4 中定義的標準平滑函式是一個凸起函式,方法如下
證明函式

包含在 中。
中。
證明函式

包含在 中。
中。
- 由此可知
 .
.
- 透過顯式計算
 ,證明
,證明 是緊緻的。
是緊緻的。
- 令
 為開集,令
為開集,令 並且令
並且令 。證明如果
。證明如果 ,那麼
,那麼 且
且  .
.
- 設
 為開集,設
為開集,設  為光滑函式,設
為光滑函式,設  。證明
。證明  。
。
- 設
 為 Schwartz 函式,設
為 Schwartz 函式,設  。證明
。證明  為 Schwartz 函式。
為 Schwartz 函式。
- 設
 ,設
,設  為多項式,設
為多項式,設  在 Schwartz 函式意義下收斂。證明
在 Schwartz 函式意義下收斂。證明  在 Schwartz 函式意義下收斂。
在 Schwartz 函式意義下收斂。







































































































































