小學數學/冪、根和指數

小學數學
← 有效數字介紹	冪、根和指數	科學記數法和工程記數法 →

指數

指數，或冪，是一種表示一個量需要乘以自身若干次的符號。在表示式 2⁵ 中，2 稱為底數，5 稱為指數或冪。2⁵ 是“將五個 2 相乘”的簡寫形式：2⁵ = 2×2×2×2×2 = 32。請注意，指數告訴我們有多少個底數相乘，而不是要執行多少次乘法。（事實上，乘法的次數比底數的次數少一次。）2⁵ 讀作“二的五次冪”或簡稱為“二的五次方”。

一般來說，

$x^{n}=\underbrace {x\cdot x\cdot x\cdot \,\,\cdots \,\,\cdot x} _{nfactors}$

其中有n 個 x需要相乘。

平方數

表示一個數乘以自身（例如 5×5）的一種便捷方法是說這個數被平方了。為了幫助你理解這一點，想象一個長 5 個單位、寬 5 個單位的正方形。那麼這個正方形的面積就是 5×5 或 25 平方單位。寫“5 的平方”的一個好方法是 5²，其中 5 稱為底數，2 稱為指數。

五行五列的面積 = 5 × 5 = 5² = 25。

完全平方數表

你可能想記住一些完全平方數

平方	結果
0²	0
1²	1
2²	4
3²	9
4²	16
5²	25
6²	36
7²	49
8²	64
9²	81
10²	100
11²	121
12²	144
13²	169
14²	196
15²	225
16²	256
17²	289
18²	324
19²	361
20²	400
21²	441
22²	484
23²	529
24²	576
25²	625
26²	676
27²	729
28²	784
29²	841
30²	900

立方數

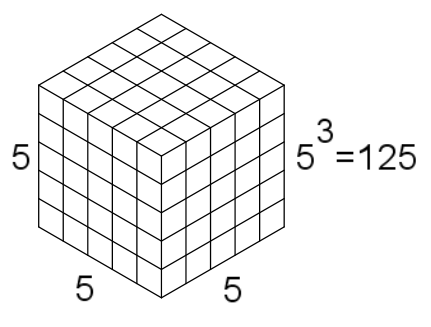
類似地，表示一個數乘以自身，然後再次乘以自身（例如 5×5×5）的一種便捷方法是說這個數被立方了。為了幫助你理解這一點，想象一個長 5 個單位、寬 5 個單位、高 5 個單位的立方體。那麼這個立方體的體積就是 5×5×5 或 125 立方單位。寫“5 的立方”的一個好方法是 5³，其中 5 稱為底數，3 稱為指數。

高、寬、長均為五的立方體的體積 = 5 × 5 × 5 = 5³ = 125。

完全立方數表

你可能想記住一些完全立方數

立方	結果
0³	0
1³	1
2³	8
3³	27
4³	64
5³	125
6³	216
7³	343
8³	512
9³	729
10³	1000

更高次冪

大於三的數字也可以用作指數，儘管對於四次冪或更高次冪的數字沒有常用的術語。例如，5⁴ = 5×5×5×5 = 625。

更高次冪表

xⁿ 表格。
底數在左側，指數在頂部
x^1/6	0	1	2	3	4	5	6	7	8	9	10	11	12...
0	?	0	0	0	0	0	0	0	0	0	0	0	0	0
1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
2	1	2	4	8	16	32	64	128	256	512	1024	2048	4096	2ⁿ
3	1	3	9	27	81	243	729	2187	6561	19683	59049			3ⁿ
4	1	4	16	64	256	1024	4096	16384	65536	262144	1048576			4ⁿ
5	1	5	25	125	625	3125	15625	78125	390625	1953125	9765625			5ⁿ
6	1	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176			6ⁿ
7	1	7	49	343	2401	16807	117649	823543	5764801	40353607	282475249			7ⁿ
8	1	8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824			8ⁿ
9	1	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401			9ⁿ
10	1	10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000			10ⁿ
11	1	11	121	1331	14641	161051	1771561	19487171	214358881	2357947691	25937424601			11ⁿ
12	1	12	144	1728	20736	248832	2985984	35831808	429981696	5159780352	61917364224			12ⁿ
13	1	13	169	2197	28561	371293	4826809	62748517	815730721	10604499373	137858491849			13ⁿ
14	1	14	196	2744	38416	537824	7529536	105413504	1475789056	20661046784	289254654976			14ⁿ
15	1	15	225	3375	50625	759375	11390625	170859375	2562890625	38443359375	576650390625			15ⁿ
16	1	16	256	4096	65536	1048576	16777216	268435456	4294967296	68719476736	1099511627776			16ⁿ	...

x	1	x	x²	x³	x⁴	x⁵	x⁶	x⁷	x⁸	x⁹	x¹⁰	x¹¹	x¹²

注意：0⁰ 未定義。

指數的性質

指數有幾個性質，這些性質經常被用來操作和簡化代數和算術表示式。

${\begin{aligned}x^{m}x^{n}&=x^{m+n}\\{\dfrac {x^{m}}{x^{n}}}&=x^{m-n}\\(xy)^{n}&=x^{n}y^{n}\\\left({\dfrac {x}{y}}\right)^{n}&={\dfrac {x^{n}}{y^{n}}}\\(x^{m})^{n}&=x^{mn}\end{aligned}}$

第一個、第三個和第五個性質可以擴充套件到多個因子，如下所示

${\begin{aligned}x^{m_{1}}x^{m_{2}}x^{m_{3}}\cdots x^{m_{n}}&=x^{m_{1}+m_{2}+m_{3}+\,\cdots \,+m_{n}}\\(x_{1}x_{2}x_{3}\cdots x_{n})^{m}&=x_{1}^{m}x_{2}^{m}x_{3}^{m}\cdots x_{n}^{m}\\(\cdots (((x^{m_{1}})^{m_{2}})^{m_{3}})\cdots )^{m_{n}}&=x^{m_{1}m_{2}m_{3}\cdots \,m_{n}}\end{aligned}}$

底數和指數為一和零

任何數的1次冪都等於它本身。例如，5¹ = 5。

任何非零數的0次冪都等於1。例如，5⁰ = 1。

0的任何正整數次冪仍然是0。例如，0⁵ = 0。

1的任何次冪仍然是1。例如，1⁵ = 1。

0的0次冪沒有定義。

負數和非整數冪

底數也可以是負數、分數或小數。這些將在本課的後面部分介紹。

根

根是冪的逆運算。

平方根

平方一個數的逆運算就是求該數的平方根。例如，25的平方根是指必須自乘才能得到25的數。在這種情況下，答案是5。這裡使用了兩種表示法

${\sqrt {25}}=25^{1/2}=5$

但是，請注意，大多數平方根不會得到整數，而且許多甚至不會產生有理數。

手動求平方根

手動求平方根的一種方法是反覆進行長除法。讓我們以求10的平方根為例。首先，我們會估計答案。由於3² = 9，而4² = 16，所以我們知道答案介於3和4之間。此外，由於10只比9大1，但比16小6，所以我們可以估計答案是3和4之間七分之一的位置。但這不會給出精確的答案，而且七分之一很難處理，所以我們改用五分之一。這樣，我們的初始估計值為3 1/5或3.2。

現在進行長除法，將10除以3.2。我們得到3.125。3.2和3.125的平均值為(3.2 + 3.125)/2 = 6.325/2 = 3.1625，因此這將是我們的下一個估計值。

現在進行長除法，將10除以3.1625。得到3.162055...（實際上我們不需要計算到比初始小數位數多一位以上）。3.1625和3.1621的平均數是3.1623，所以我們將3.1623作為下一次估計值。

現在進行長除法，將10除以3.1623。得到3.162255...

因此，可以重複此方法以獲得所需的精度。10的實際平方根是3.16227766...

請注意，大多數平方根計算使用計算器或計算機，但瞭解如何手動計算平方根在沒有計算器的情況下非常有用。

如果你想自己嘗試這種方法，可以嘗試求7的平方根。

立方根

將一個數立方後的逆運算就是求該數的立方根。例如，125的立方根是指必須自乘三次才能得到125的數。在本例中，答案是5。這裡使用了兩種型別的表示法

${\sqrt[{3}]{125}}=125^{1/3}=5$

但是，請注意，大多數立方根的結果都不是整數，而且很多甚至不是有理數。

高次根

大於3的數也可以用作根，儘管四次根或更高次根沒有常用的術語。例如

${\sqrt[{4}]{625}}=625^{1/4}=5$

但是，請注意，大多數高次根的結果都不是整數，而且很多甚至不是有理數。

冪和根的結合

之前用於根的單位分數表示法可能讓你想到，根實際上與冪相同，只是指數為單位分數（某個數的倒數），而不是整數。因此，分數表示法在高等數學中實際上更受歡迎，儘管根號仍然偶爾使用，尤其是在平方根中。

分數作為指數

其他（非單位）分數也可以用作指數。在這種情況下，底數可以先升到分子（分數的上部）的冪，然後使用分母（分數的下部）來開根。例如

$8^{2/3}={\sqrt[{3}]{8^{2}}}={\sqrt[{3}]{64}}=4$

或者，可以先開根，然後再應用冪

$8^{2/3}=({\sqrt[{3}]{8}})^{2}=2^{2}=4$

小數指數

任何分數指數也可以表示為小數指數。例如，平方根也可以寫成

$25^{1/2}=25^{0.5}=5\;$

此外，不能表示為分數的小數（無理數）也可以用作指數

$5^{3.1415926...}=156.99...\;$

這類問題用基本的數學技能很難手動解決，但可以手動估計答案。在本例中，由於3.1415926介於3和4之間（並且更接近3），因此我們知道答案將介於5^3（或125）和5^4（或625）之間，並且更接近125。

負指數

負指數僅僅意味著你首先取底數的倒數（1除以該數），然後應用指數

$25^{-0.5}=1/25^{0.5}=1/5\;$

或者，你可以先計算指數（忽略符號），然後取倒數。

$25^{-0.5}=5^{-1}=1/5\;$

分數作為底數

當分數被提升到某個指數時，分子和分母都將被提升到該指數。

$(5/6)^{2}=5^{2}/6^{2}=25/36\;$

分數也可以同時用作底數和指數。

$(25/36)^{1/2}=25^{1/2}/36^{1/2}=5/6\;$

此外，也可以使用負分數指數，像往常一樣取底數的倒數來求解。

$(25/36)^{-1/2}=(36/25)^{1/2}=36^{1/2}/25^{1/2}=6/5\;$

負數作為底數

對於整數冪，負數底數可以像正常一樣處理。

$(-5)^{2}=(-5)\times (-5)=25\;$

$(-5)^{3}=(-5)\times (-5)\times (-5)=-125\;$

$(-5)^{4}=(-5)\times (-5)\times (-5)\times (-5)=625\;$

$(-5)^{5}=(-5)\times (-5)\times (-5)\times (-5)\times (-5)=-3125\;$

請注意，負數底數提升到偶數冪會產生正數結果，而負數底數提升到奇數冪會產生負數結果。

注意負號。由於 -5 = -1×5， $-5^{2}$ 和 $(-5)^{2}$ 之間是有區別的。前者表示 5 乘以 5 的結果取負，而後者
表示 -5 的平方。換句話說，

$-5^{2}=-1\times 5^{2}=-1\times (5\times 5)=-1\times 25=-25$

但是

$(-5)^{2}=(-5)\times (-5)=25$

根和分數/小數冪稍微複雜一些。奇數次根運算結果良好

$(-125)^{1/3}=-5\;$

然而，偶數次根沒有實數解

$(-25)^{1/2}=?\;$

$(-625)^{1/4}=?\;$

請注意，沒有一個實數自乘後等於 -25，因為 5×5 = 25 且 -5×-5 = 25。實際上存在一個解，稱為**虛數**，但將在以後的課程中討論。

主根

請注意，由於 5×5 = 25 和 -5×-5 = 25，當我們被要求求 25 的平方根時，實際上有兩個有效的答案，5 和 -5。實際上，任何正數的偶數次根都有兩個解，其中一個為另一個的負數。這可能看起來不尋常，但在高等數學中，問題通常有多個解。

但是，對於許多問題，只有正值在物理上有效。例如，如果我們被要求計算一個面積為 25 平方單位的正方形院子邊長的長度，則只有 5 個單位的邊長有效。如果我們說“每條邊也可以有 -5 個單位的長度”，那沒有任何意義。因此，正解稱為**主根**，並且根據問題的不同，可能是唯一需要的答案。在兩個答案都有效的場合，有時寫成 ±5（讀作“正負五”）。但是，x 平方平方根的數學定義是 x 的絕對值。因此，平方根方程沒有兩個答案，但兩個數字的平方可以等於相同的 rational number。

小學數學
← 有效數字介紹	冪、根和指數	科學記數法和工程記數法 →