Note: I have not checked this thoroughly.
數學中最熟悉的實體 之一是數字 。從學齡前到高階水平,數字 與數學息息相關。但在數學上,這些數字 是什麼?本節將展示數學家如何構建數系。我們將從集合論的公理(ZFC 集合論)開始,並以純粹的集合論方法來構建數字 。
N {\displaystyle \mathbb {N} } [ 編輯 | 編輯原始碼 ] 有了這些公理,我們就可以開始構建數字。我們的重點是快速啟動並構建所有常用的數字。因此,我們不會專注於開發集合所具有的所有屬性,而是相信使用者會同意我們的構造足夠健全,並且所有屬性的嚴格證明都確實存在於這些公理中。
我們的第一個目標是構建基本的計數數字,也稱為自然數。無窮公理說存在一個集合X ,它滿足包含空集和集合的屬性,以及當一個集合y 是X 的成員時, S ( y ) {\displaystyle S(y)\!} X 的成員。可能存在也可能不存在其他此類集合。取所有此類集合的交集,我們得到自然數集N 。顯然,它是最小集合。同樣,由於 ∅ {\displaystyle \varnothing } N 的成員,因此是, { ∅ } {\displaystyle \{\varnothing \}} { ∅ { ∅ } } {\displaystyle \{\varnothing \,\{\varnothing \}\}} N 是最小的集合。我們令 0 = ∅ {\displaystyle 0=\varnothing } 1 = { ∅ } {\displaystyle 1=\{\varnothing \}} 2 = { ∅ { ∅ } } {\displaystyle 2=\{\varnothing \,\{\varnothing \}\}}
因此,我們從數學上定義了自然數集。我們將如下定義自然數的加法和乘法:令 x + = S ( x ) {\displaystyle x^{+}=S(x)\!} a + ( b + ) = ( a + b ) + {\displaystyle a+(b^{+})=(a+b)^{+}} 1 + 1 = 1 + 0 + = ( 1 + 0 ) + = 1 + = 2 {\displaystyle 1+1=1+0^{+}=(1+0)^{+}=1^{+}=2} 0 + = 1 {\displaystyle 0^{+}=1}
我們再次假設讀者信任我們,當我們說所有自然數的通常性質都可以在我們構建的自然數系統中建立時,我們再次邁出了一步。我們在這裡避免這樣做是因為我們希望避免陷入正式論證,並偏離我們的目標,即快速地對數字進行數學構建。
接下來我們處理整數。由於我們需要在我們的工具箱中使用一些簡短的無關概念(所有這些概念都是根據集合論公理定義的,並且它們的性質也與之一致),我們將簡要提到這些概念。首先是序偶 (a,b) 的概念,它被定義為集合 {{a},{a,b}},使用它可以定義 3 元組 (a,b,c) 為序偶 (a,(b,c)),即 {{a}{{b},{b,c}}}。類似地,可以定義 4 元組、5 元組等。接下來是函式和關係的概念,我們相信讀者從微積分中瞭解這些概念。最後,我們討論等價關係和等價類。
給定集合 *A* 上的一個關係 ~ 被稱為等價關係,當且僅當它具有自反性、對稱性和傳遞性。等價地,對於 *A* 中的所有 *a*、*b* 和 *c*,
*a* ~ *a*。(自反性)
如果 *a* ~ *b*,則 *b* ~ *a*。(對稱性)
如果 *a* ~ *b* 且 *b* ~ *c*,則 *a* ~ *c*。(傳遞性) *a* 在 ~ 下的等價類,記為 [*a*],被定義為 [ a ] = { b ∈ A | a ∼ b } {\displaystyle [a]=\{b\in A|a\sim b\}}
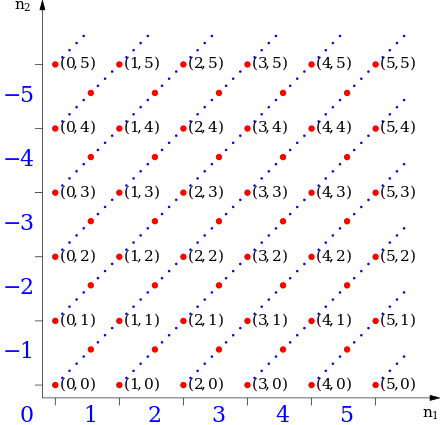
紅點表示自然數的有序對。連線的紅點是等價類,表示線末端的藍色整數。 現在,整數集可以正式定義為特定關係的等價類集。該關係是在自然數的有序對之間定義的(不是在自然數本身之間,而是在它們的對之間)。
直覺是 ( *a*,*b* ) 代表從 *a* 中減去 *b* 的結果。為了證實我們的預期,即1 − 2 和4 − 5 表示同一個數字,我們根據以下規則在這些對上定義了一個等價關係 ~
( a , b ) ∼ ( c , d ) {\displaystyle (a,b)\sim (c,d)\,\!} 當且僅當
a + d = b + c . {\displaystyle a+d=b+c.\,\!} 整數的加法和乘法可以根據自然數上的等效運算來定義;用 [( *a*,*b* )] 表示包含 ( *a*,*b* ) 作為成員的等價類,我們有
[ ( a , b ) ] + [ ( c , d ) ] := [ ( a + c , b + d ) ] . {\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].\,} [ ( a , b ) ] ⋅ [ ( c , d ) ] := [ ( a c + b d , a d + b c ) ] . {\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].\,} 整數的否定(或加法逆元)是透過顛倒對的順序獲得的
− [ ( a , b ) ] := [ ( b , a ) ] . {\displaystyle -[(a,b)]:=[(b,a)].\,} 因此,減法可以定義為加法逆元的加法
[ ( a , b ) ] − [ ( c , d ) ] := [ ( a + d , b + c ) ] . {\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].\,} 整數的標準排序由以下給出
[ ( a , b ) ] < [ ( c , d ) ] {\displaystyle [(a,b)]<[(c,d)]\,} a + d < b + c . {\displaystyle a+d<b+c.\,} 很容易驗證這些定義與等價類代表的選擇無關。
每個等價類都有一個唯一的成員,其形式為 (n ,0) 或 (0,n )(或兩者兼有)。自然數 n 與類 [(n ,0)] 識別(換句話說,自然數被嵌入到整數中,透過將 n 對映到 [(n ,0)]),而類 [(0,n )] 被表示為 −n (這涵蓋了所有剩餘的類,並且為類 [(0,0)] 提供了第二個時間,因為 −0 = 0。)
因此,[(a ,b )] 被表示為
{ a − b , if a ≥ b − ( b − a ) , if a < b . {\displaystyle {\begin{cases}a-b,&{\mbox{if }}a\geq b\\-(b-a),&{\mbox{if }}a<b.\end{cases}}} 如果自然數被識別為相應的整數,這種約定不會產生歧義。
這種表示法恢復了整數的熟悉表示法,即 {... −3,−2,−1, 0, 1, 2, 3, ...}。
一些例子是
0 = [ ( 0 , 0 ) ] = [ ( 1 , 1 ) ] = ⋯ = [ ( k , k ) ] 1 = [ ( 1 , 0 ) ] = [ ( 2 , 1 ) ] = ⋯ = [ ( k + 1 , k ) ] − 1 = [ ( 0 , 1 ) ] = [ ( 1 , 2 ) ] = ⋯ = [ ( k , k + 1 ) ] 2 = [ ( 2 , 0 ) ] = [ ( 3 , 1 ) ] = ⋯ = [ ( k + 2 , k ) ] − 2 = [ ( 0 , 2 ) ] = [ ( 1 , 3 ) ] = ⋯ = [ ( k , k + 2 ) ] . {\displaystyle {\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)].\end{aligned}}} 下一站:有理數!
那些學習過代數課程的人可能會認識到下面的構造,正是透過這種構造,一個整環被嵌入到一個域中。(事實上,這並不奇怪,因為整數形成一個整環,而有理數形成一個域。)對於那些認為域是開闊空間,並且在考慮農業而不是農業的人來說,不用擔心。我們在下面提供了完整的構造。
一個圖表,顯示了整數對等價類的表示 在數學上,構造類似於我們從自然數構造整數時所做的。我們考慮所有整數有序對 (m ,n ) 之間的以下關係,其中 n ≠ 0。具體來說,關係是 (m 1 ,n 1 ) ~ (m 2 ,n 2 ) 當且僅當 m 1 n 2 − m 2 n 1 = 0。
( m 1 , n 1 ) + ( m 2 , n 2 ) := ( m 1 n 2 + n 1 m 2 , n 1 n 2 ) {\displaystyle \left(m_{1},n_{1}\right)+\left(m_{2},n_{2}\right):=\left(m_{1}n_{2}+n_{1}m_{2},n_{1}n_{2}\right)} ( m 1 , n 1 ) × ( m 2 , n 2 ) := ( m 1 m 2 , n 1 n 2 ) {\displaystyle \left(m_{1},n_{1}\right)\times \left(m_{2},n_{2}\right):=\left(m_{1}m_{2},n_{1}n_{2}\right)} 並且,如果 m 2 ≠ 0,則除以
( m 1 , n 1 ) ( m 2 , n 2 ) := ( m 1 n 2 , n 1 m 2 ) . {\displaystyle {\frac {\left(m_{1},n_{1}\right)}{\left(m_{2},n_{2}\right)}}:=\left(m_{1}n_{2},n_{1}m_{2}\right).} 等價關係 (m 1 ,n 1 ) ~ (m 2 ,n 2 ) 當且僅當 m 1 n 2 − m 2 n 1 = 0Q 為該關係下所有等價類的集合。我們用 [(m 1 ,n 1 )] 表示包含 (m 1 ,n 1 ) 的等價類。如果 (m 1 ,n 1 ) ~ (m 2 ,n 2 ),則根據定義,(m 1 ,n 1 ) 屬於 [(m 2 ,n 2 )],而 (m 2 ,n 2 ) 屬於 [(m 1 ,n 1 )];在這種情況下,我們可以寫 [(m 1 ,n 1 )] = [(m 2 ,n 2 )]。對於任何等價類 [(m ,n )],都有無窮多個表示形式,因為
⋯ = [ ( − 2 m , − 2 n ) ] = [ ( − m , − n ) ] = [ ( m , n ) ] = [ ( 2 m , 2 n ) ] = ⋯ . {\displaystyle \cdots =[(-2m,-2n)]=[(-m,-n)]=[(m,n)]=[(2m,2n)]=\cdots .} [(m ,n )] 的規範選擇是使 gcd(m ,n ) = 1,即 m 和 n 沒有公因子,即 m 和 n 互質。例如,我們會寫 [(1,2)] 而不是 [(2,4)] 或 [(−12,−24)],即使 [(1,2)] = [(2,4)] = [(−12,−24)]。
整數可以透過將 m 對映到 [(m , 1)] 的嵌入被視為有理數。
實數在等著我們!
首先,我們需要德德金分割的概念。德德金分割,以理查德·德德金命名,是有理數的一個劃分,將其分成兩個非空部分 A 和 B,使得 A 中的所有元素都小於 B 中的所有元素,並且 A 不包含最大元素。分割本身在概念上是 A 和 B 之間定義的“間隙”。換句話說,A 包含所有小於分割的有理數,而 B 包含所有大於分割的有理數。
為了方便起見,我們可以將較低集合 A 作為任何給定德德金分割 A,B 的代表,因為 A 完全決定了 B。我們現在定義實數集為所有德德金分割的集合。更詳細地說,一個實數 r {\displaystyle r} Q {\displaystyle {\textbf {Q}}}
r {\displaystyle r} r ≠ Q {\displaystyle r\neq {\textbf {Q}}} r 向下閉合。換句話說,對於所有 x , y ∈ Q {\displaystyle x,y\in {\textbf {Q}}} x < y {\displaystyle x<y} y ∈ r {\displaystyle y\in r} x ∈ r {\displaystyle x\in r} r 沒有最大元素。換句話說,不存在 x ∈ r {\displaystyle x\in r} y ∈ r {\displaystyle y\in r} y ≤ x {\displaystyle y\leq x} 我們形成實數集 R {\displaystyle {\textbf {R}}} Q {\displaystyle {\textbf {Q}}} A {\displaystyle A} 我們將有理數嵌入到實數中,透過將有理數 q {\displaystyle q} { x ∈ Q : x < q } {\displaystyle \{x\in {\textbf {Q}}:x<q\}} 加法。 A + B := { a + b : a ∈ A ∧ b ∈ B } {\displaystyle A+B:=\{a+b:a\in A\land b\in B\}} 定義乘法就不那麼直接了。如果 A , B ≥ 0 {\displaystyle A,B\geq 0} A × B := { a × b : a ≥ 0 ∧ a ∈ A ∧ b ≥ 0 ∧ b ∈ B } ∪ { x ∈ Q : x < 0 } {\displaystyle A\times B:=\{a\times b:a\geq 0\land a\in A\land b\geq 0\land b\in B\}\cup \{x\in \mathrm {Q} :x<0\}}
如果 A {\displaystyle A\,} B {\displaystyle B\,} A × B = − ( A × − B ) = − ( − A × B ) = ( − A × − B ) {\displaystyle A\times B=-(A\times -B)=-(-A\times B)=(-A\times -B)\,} A {\displaystyle A\,} B {\displaystyle B\,} 我們做完了嗎?還沒有。讀者無疑已經遇到的複數集還在等待我們。幸運的是,它不需要像實數那樣詳細的展開,我們很快就可以得到它,方法如下。
設 C 為實數的有序對 (a , b ) 的集合 R 2 。C 被定義為複數集。在這種表示法中,加法和乘法的上述公式寫為
( a , b ) + ( c , d ) = ( a + c , b + d ) {\displaystyle (a,b)+(c,d)=(a+c,b+d)\,} ( a , b ) ⋅ ( c , d ) = ( a c − b d , b c + a d ) {\displaystyle (a,b)\cdot (c,d)=(ac-bd,bc+ad)\,} 然後,將 (a, b) 表示為 a + ib 僅僅是一個符號問題。加法和乘法是自然定義的。
← 關係 · 排序 →














![{\displaystyle [a]=\{b\in A|a\sim b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecd447db4dc0435369173860cd769d704aab0a86)


![{\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfcba304a40eefc1e283a196d969ce6fa683cceb)
![{\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fd52f4eb8780650b373d9344ef67d9d7dbd82aa)
![{\displaystyle -[(a,b)]:=[(b,a)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d87f0da3470a1aa6e060178fe742c78a559c72f4)
![{\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c83020bdeb7849794e886ea622e66a1dd4ae76)
![{\displaystyle [(a,b)]<[(c,d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b572331cb7640ad3bb18ece2afea1a790b27a3eb)


![{\displaystyle {\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/325c6a83a84e4fe08bac03e453f674b1ff83eac1)



![{\displaystyle \cdots =[(-2m,-2n)]=[(-m,-n)]=[(m,n)]=[(2m,2n)]=\cdots .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e24a266d671aacfa9b28f50c572f733d630b72c)



















