狹義相對論/相對性原理

相對性原理

伽利略·伽利雷

相對性原理探討了在不同地點進行觀察之間的關係。這個問題自古以來就是一個艱難的理論挑戰，涉及物理問題，例如物體的速度如何組合以及影響如何在運動物體之間傳遞。

解決這個問題最有效的方法之一是研究觀察者速度對觀察的影響。這個問題曾被古典哲學家們解決過，但伽利略的工作取得了真正的突破。 伽利略 (1632) 在他的 關於兩大世界體系的對話 中，考慮了船內的人所做的運動觀察，他們看不到船外

"讓船以你喜歡的任何速度前進，只要運動是均勻的，而不是這樣那樣地波動。你將發現所有提到的效應沒有發生絲毫變化，你也不會從其中任何一個效應中判斷出船是在運動還是靜止的。"

根據伽利略，如果船平穩移動，那麼船內的人就無法判斷他們是否在移動。如果伽利略在移動的船上的人正在吃晚飯，他們會看到他們的豌豆從叉子上直直地掉到他們的盤子裡，就像他們在陸地上家裡一樣。豌豆隨著人們一起移動，對就餐者來說不會看起來是斜著掉落的。這意味著豌豆保持勻速運動狀態，除非有人攔截它們或以其他方式作用於它們。這也意味著人們在船上進行的簡單實驗在船上或在家裡會得到相同的結果。這個概念導致了“伽利略相對論”，它認為物體除非受到作用，否則將保持運動狀態，並且物理定律與實驗室的速度無關。

這個簡單的想法挑戰了之前亞里士多德的觀點。 亞里士多德 在他的《物理學》中 認為物體必須要麼被移動要麼處於靜止狀態。根據亞里士多德的說法，基於對“虛空”可能性複雜而有趣的論證，物體在沒有東西推動的情況下不能保持運動狀態。因此，亞里士多德認為物體會在空曠的空間中完全停止。如果亞里士多德是正確的，那麼你在移動的船上吃飯時掉落的豌豆會落在你的腿上，而不是直直地掉到你的盤子上。亞里士多德的觀點被所有人接受，因此伽利略的新提議是異乎尋常的，並且因為它幾乎是正確的，所以它成為了物理學的基礎。

伽利略相對論包含兩個重要原則：首先，不可能確定誰實際上處於靜止狀態；其次，物體除非受到作用，否則將保持勻速運動狀態。第二個原則被稱為伽利略慣性定律或牛頓第一運動定律。

狹義相對論

直到 19 世紀，伽利略相對論似乎認為所有觀察者都是等價的，無論他們移動的速度有多快。如果你在北極向上拋一個球，它會直直地落下來，這在赤道上也會發生，儘管赤道比極點快近一千英里。伽利略速度是可加的，因此當你在赤道向上拋球時，球會以一千英里的速度繼續運動，並且會繼續以這個速度運動，直到它受到外部作用力的作用。

這個簡單的方案在 1865 年被詹姆斯·克萊克·麥克斯韋發現的描述光等電磁波傳播的方程所質疑。他的方程表明光速取決於被認為是充滿所有空間的物理介質或“以太”的簡單特性的常數。如果是這種情況，那麼根據伽利略相對論，應該可以將你自己的速度加到入射光的速度上，因此，如果你以光速的一半速度旅行，那麼任何朝你射來的光都會被觀察到在以太中以 1.5 倍的光速旅行。同樣，任何從你身後射來的光都會以以太中光速的 0.5 倍的速度撞擊你。光本身始終以以太中的相同速度傳播，因此如果你在高速行駛時用電筒照射光，光會進入以太並減慢到它的正常速度。這將破壞伽利略的相對論，因為你只需要做的一件事就是測量不同方向的光速來發現你是在移動的船上還是在陸地上。光在你透過以太的運動方向上會變慢，而在相反方向上會變快。

如果麥克斯韋方程是有效的，並且簡單的經典速度加法適用，那麼應該存在一個優先參考系，即靜止以太的框架。優先參考系將被認為是所有速度測量都可以參考的真實零點。

狹義相對論透過保持麥克斯韋方程是正確的，但經典速度加法是錯誤的，從而恢復了物理學中的相對性原理：不存在優先參考系。狹義相對論恢復了以下解釋：在所有慣性參考系中，相同的物理現象正在發生，並且不存在允許觀察者確定速度零點的現象。 愛因斯坦 透過提出物理定律與觀察者的速度無關，從而保留了相對性原理。根據愛因斯坦的說法，無論你是在伽利略船的貨艙裡，還是在以光速很大一部分速度執行的宇宙飛船的貨艙裡，物理定律都將是相同的。

愛因斯坦的想法與伽利略的想法具有相同的哲學，兩人都相信物理定律不會受到勻速運動的影響。在伽利略和愛因斯坦之間的歲月裡，人們認為正是速度簡單地相互加成的方式保留了物理定律，但愛因斯坦調整了這個簡單概念，以允許麥克斯韋方程成立。

參考系、事件和變換

在進一步分析相對運動之前，需要更仔細地定義參考系、事件和變換的概念。

物理觀察者被認為被參考系包圍，參考系是一組座標軸，用它可以指定位置或運動，或者用它可以數學地描述物理定律。

事件是指獨立於可能用於描述它的參考系而發生的事情。開啟一盞燈或兩個物體的碰撞將構成一個事件。

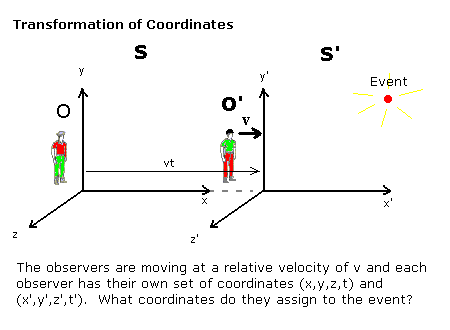
假設有一個小事件，例如開啟一盞燈，它在一個參考系中的座標為 $x,y,z,t$。另一個觀察者在另一個參考系中以速度 $v$ 相對於第一個參考系沿著 $x$ 軸移動，會將事件分配給事件什麼座標呢？這個問題在下面進行了說明

我們正在尋找的是事件 $x^{'},y^{'},z^{'},t^{'}$ 的第二個觀察者座標與事件 $x,y,z,t$ 的第一個觀察者座標之間的關係。座標指的是每個觀察者測量的事件的位置和時間，為了簡單起見，觀察者被安排在 $t=0$ 時重合。

根據伽利略相對論

$x^{'}$ $=x-vt$

$y^{'}$ = $y$

$z^{'}$ = $z$

$t^{'}$ = $t$

這組方程被稱為伽利略座標變換或伽利略變換。

這些方程表明，在一個參考系中事件的位置如何與另一個參考系中事件的位置相關。但如果事件是正在移動的東西，會發生什麼呢？速度如何從一個框架轉換到另一個框架呢？

速度的計算依賴於牛頓公式：$v=dx/dt$。使用牛頓物理學來計算速度和其他物理變數，導致伽利略相對論在得出超出簡單座標變化的結論時被稱為牛頓相對論。根據伽利略相對論，三個空間方向上的速度變換為

$\mathbf {u_{x}^{'}=u_{x}-v}$

$\mathbf {u_{y}^{'}=u_{y}}$

其中 $\mathbf {u_{x}^{'},u_{y}^{'},u_{z}^{'}}$ 是第二個觀察者記錄的運動物體在空間三個方向上的速度，而 $\mathbf {u_{x},u_{y},u_{z}}$ 是第一個觀察者記錄的速度，而 $\mathbf {v}$ 是兩個觀察者的相對速度。 $\mathbf {v}$ 前面的減號表示運動物體正在遠離兩個觀察者。

這個結果被稱為經典速度加法定理，它總結了兩個伽利略參考系之間的速度變換。這意味著，必須根據拋射體源頭和目標的速度來確定拋射體的速度。例如，如果一個水手從伽利略的船上以 10 公里/小時的速度向岸邊扔一塊石頭，而伽利略的船以 5 公里/小時的速度向岸邊移動，那麼石頭擊中岸邊時將以 15 公里/小時的速度移動。

在牛頓相對論中，空間幾何被認為是歐幾里得的，所有觀察者的時間測量都被認為是相同的。

經典速度加法定理的推導如下。
如果伽利略變換對時間進行微分

$x^{'}=x-vt$

所以

$dx^{'}/dt=dx/dt-v$

但在伽利略相對論中，$t^{'}=t$，所以 $dx^{'}/dt^{'}=dx^{'}/dt$ 因此

$dx^{'}/dt^{'}=dx/dt-v$

$dy^{'}/dt^{'}=dy/dt$

$dz^{'}/dt^{'}=dz/dt$

如果我們寫 $u_{x}^{'}=dx^{'}/dt^{'}$ 等，那麼

$u_{x}^{'}=u_{x}-v$

$u_{y}^{'}=u_{y}$

$u_{z}^{'}=u_{z}$

狹義相對論的假設

上一節描述了從一個參考系到另一個參考系的轉換，使用的是伽利略時代提出的簡單速度疊加。這些轉換與伽利略的主要假設一致，即物理定律對所有慣性觀察者都是相同的，因此沒有人能夠分辨誰是靜止的。以太理論對伽利略的假設提出了質疑，因為以太是靜止的，觀察者可以透過測量光在運動方向上的速度來判斷自己是否靜止。愛因斯坦保留了伽利略的基本假設，即物理定律在所有慣性參考系中都是相同的。但為了做到這一點，他必須引入一個新的假設，即光速對所有觀察者都是相同的。這些假設列舉如下

1. 第一個假設：相對性原理

正式表述：物理定律在所有慣性參考系中都是相同的。

非正式表述：任何物理理論對每個慣性觀察者來說，在數學上都應該是一樣的。在一個圍繞太陽和銀河系執行的宇宙飛船或星球上的物理實驗室進行的實驗將給出相同的結果，無論實驗室的速度有多快。

2. 第二個假設：光速不變性

正式表述：在所有慣性參考系中，自由空間中的光速都是一個常數。

非正式表述：真空中光速，通常用c表示，對所有慣性觀察者來說都是相同的；在所有方向都是相同的；並且不依賴於發射光的物體速度。

使用這些假設，愛因斯坦能夠計算出事件的觀測結果如何取決於觀察者的相對速度。然後，他能夠構建一個物理理論，並由此產生了一些預言，比如質量和能量的等價性以及早期的量子理論。

愛因斯坦對相對論公理的表述被稱為電動力學方法。在大多數高階教科書中，它已被時空方法所取代，在時空方法中，物理定律本身是由於時空中的對稱性造成的，而光速的恆定性則是時空存在的自然結果。然而，愛因斯坦的方法同樣有效，它代表了一次演繹推理的壯舉；它為現代處理該主題提供了必要的洞察力。

愛因斯坦的相對論——電動力學方法

愛因斯坦問，如果兩個觀察者都發現光速是恆定的，那麼他們測量的長度和時間可能需要如何變化？他觀察了兩個觀察者用來計算光速的公式，$(x=ct)$和$(x^{'}=ct^{'})$，並詢問需要引入哪些常數才能保持光速的測量值保持相同，即使觀察者的相對運動意味著$x^{'}$軸不斷前進。他的工作在附錄中詳細展示。這個計算的結果是洛倫茲變換方程

$x'=\gamma (x-vt)\,$

$y'=y\,$

$z'=z\,$

$t'=\gamma (t-{\frac {vx}{c^{2}}})\,$

其中常數 $\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$。這些方程適用於任何兩個相對運動的觀察者，但請注意括號內的符號會根據速度的方向而改變 - 請參見附錄。

洛倫茲變換相當於伽利略變換，只是增加了每個人都測量到相同的光速的假設，無論他們運動的速度有多快。光速是距離與時間的比率（即：米每秒），因此對於每個人來說，測量到的光速值都相同，測量桿的長度、光源和接收器之間的空間長度以及時鐘的滴答次數必須在觀察者之間動態地有所不同。只要長度和時間間隔隨兩個觀察者的相對速度 (v) 變化，如洛倫茲變換所描述的那樣，觀察者都可以將光速計算為光線傳播的距離與傳播該距離所花費的時間之比，並得到相同的值。

愛因斯坦的方法是“電動力學”的，因為它假設，根據麥克斯韋方程組，光以恆定速度傳播。如上所述，普遍恆定速度的概念很奇怪，因為速度是距離與時間的比率。洛倫茲變換方程是否掩蓋了關於空間和時間的更深層的真相？愛因斯坦本人 對洛倫茲變換方程是如何實際描述空間和時間本身的性質給出了最清晰的描述之一。他的總體推理如下。

如果將這些方程組合起來，它們滿足以下關係

(1) $x^{'2}-c^{2}t^{'2}=x^{2}-c^{2}t^{2}\,$

愛因斯坦 (1920) 描述瞭如何將其擴充套件以描述在空間中任何方向上的運動

(2) $x^{'2}+y^{'2}+z^{'2}-c^{2}t^{'2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}\,$

方程 (2) 是關於宇宙中長度和時間關係的幾何公理。它表明存在一個常數 s，使得

$s^{2}=x^{'2}+y^{'2}+z^{'2}-c^{2}t^{'2}\,$

$s^{2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}\,$

這個方程被閔可夫斯基認為是畢達哥拉斯定理（即 $s^{2}=x^{2}+y^{2}$）的擴充套件，這種擴充套件在 20 世紀初的數學中是眾所周知的。洛倫茲變換告訴我們，宇宙是一個四維時空，因此不需要任何“以太”。（參見愛因斯坦 1920，附錄，瞭解愛因斯坦關於洛倫茲變換如何表明一個四維宇宙的討論，但請注意，“虛時間”現在已被“度量張量”的使用所取代）。

愛因斯坦的分析表明，兩個相對運動的觀察者的 x 軸和時間軸不會重疊。將一個觀察者的時間與另一個觀察者的時間聯絡起來的方程表明，這種關係隨 x 軸上的距離而變化，即

$t'=\gamma (t-{\frac {vx}{c^{2}}})\,$

這意味著“參考系”的整個概念需要重新審視，以允許軸不再重疊的方式。

慣性參考系

洛倫茲變換對時間的變換涉及一個分量 $(vx/c^{2})$，這導致沿相對移動的觀察者的 x 軸的時間測量值不同。這意味著不再適用簡單地涉及三個空間維度且所有觀察者共享相同的時間的參考系的概念。要比較觀察者之間的測量值，必須將“參考系”的概念擴充套件到包括觀察者的時鐘。

慣性參考系是一個概念上的三維格架，由相互垂直的測量桿組成，在每個點上都有相互同步的時鐘（有關完整定義，請參見下文）。定義為屬於或連線到慣性參考系的物體，是一個不干擾時鐘同步並保持在參考系內恆定空間位置的物體。與運動的非旋轉物體相連或附著的慣性參考系被稱為該物體的慣性靜止系。對於特定物體，慣性參考系是該物體的靜止系，當由相對運動的觀察者觀察時，它會隨著物體一起運動。

這種型別的參考系被稱為“慣性”參考系，因為，如將在本書後面看到的那樣，每個根據牛頓慣性定律（沒有旋轉、引力場或作用力）共同運動的物體系統都有一個共同的靜止系，其時鐘同步和杆長度與其他相對運動的靜止系中的時鐘和杆不同。

關於“慣性參考系”有很多其他的定義，但大多數定義，比如“慣性參考系是牛頓第一定律有效的參考系”，都沒有提供關於座標如何排列和/或代表從更基本定義推匯出的必要細節。

Blandford 和 Thorne（2004）給出的以下定義是對工作物理學家所指的慣性參考系的相當完整的總結。

“慣性參考系是一個（概念上的）三維的測量桿和時鐘網路，具有以下性質：（i）該網路在時空中自由移動（即不受任何力的作用），並且連線到陀螺儀上，因此它不會相對於遙遠的宇宙天體旋轉。 （ii）測量桿形成一個正交網路，並且刻在它們上面的長度間隔在與例如由某種型別的標準原子或分子發射的光的波長相比時是均勻的；因此，杆形成了一個正交的笛卡爾座標系，其中座標x沿著一個軸測量，y沿著另一個軸測量，z沿著第三個軸測量。（iii）時鐘密集地分佈在整個網路中，因此，理想情況下，在每個網路點都有一個單獨的時鐘。 （iv）與例如某種型別的標準原子或分子發射的光的週期相比，這些時鐘的滴答聲是均勻的；即它們是理想的時鐘。 （v）時鐘透過愛因斯坦同步過程同步：如果一個時鐘發射的光脈衝從連線到另一個時鐘的鏡子反射回來，然後返回，則反彈時間$t_{b}$由進行反彈的時鐘測量，是發射和接收時間的一半，由發射和接收時鐘測量：$t_{b}=1/2(t_{e}+t_{r})$。¹

¹有關理想時鐘和理想測量桿性質的更深入討論，請參閱例如 Misner、Thorne 和 Wheeler（1973）的第 23-29 頁和 395-399 頁。

狹義相對論表明，相對於彼此運動的物體的慣性靜止系不會重疊。每個觀察者都看到另一個運動觀察者的慣性參考系發生了扭曲。這一發現是狹義相對論的本質，意味著在運動的觀察者之間，座標和其他測量的轉換非常複雜。將在下面深入討論。