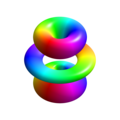雖然德布羅意在 1923 年的理論提出了圓形電子波,但薛定諤在 1926 年的“波動力學”提出了三維空間的駐波。找到它們意味著找到時間無關薛定諤方程的解

其中  是經典電子在距離
是經典電子在距離  處質子的勢能。(只有當我們進入相對論理論時,我們才能擺脫經典思維的最後殘餘。)
處質子的勢能。(只有當我們進入相對論理論時,我們才能擺脫經典思維的最後殘餘。)

在使用這個方程時,我們忽略了 (i) 電子對質子的影響,質子的質量是電子的 1836 倍,(ii) 電子的自旋。由於相對論和自旋對原子氫的可測量性質的影響相當小,因此這種非相對論近似仍然能給出非常好的結果。
對於束縛態,總能量  為負,薛定諤方程有一組離散解。結果證明,
為負,薛定諤方程有一組離散解。結果證明, 的“允許”值正是玻爾在 1913 年獲得的值
的“允許”值正是玻爾在 1913 年獲得的值

然而,對於每個 ,現在有
,現在有 個線性無關的解。(如果
個線性無關的解。(如果 是獨立的解,那麼它們中沒有一個可以寫成其他解的線性組合
是獨立的解,那麼它們中沒有一個可以寫成其他解的線性組合 。)
。)
具有不同 的解對應於不同的能量。哪些物理差異對應於具有相同
的解對應於不同的能量。哪些物理差異對應於具有相同 的線性無關解?
的線性無關解?

使用極座標,發現對於特定值 的所有解都是具有以下形式的解的線性組合:
的所有解都是具有以下形式的解的線性組合:

 發現是另一個量子化變數,因為
發現是另一個量子化變數,因為 意味著
意味著 ,其中
,其中 。此外,
。此外, 存在上限,我們稍後會看到。
存在上限,我們稍後會看到。
正如將 分解為
分解為  使得可以獲得一個
使得可以獲得一個 無關的薛定諤方程,因此將
無關的薛定諤方程,因此將 分解為
分解為  使得可以獲得一個
使得可以獲得一個 無關的薛定諤方程。這包含另一個實引數
無關的薛定諤方程。這包含另一個實引數 除了
除了  其 “允許” 值由
其 “允許” 值由  給出,其中
給出,其中  是滿足
是滿足  的整數。
的整數。  可能值的範圍受不等式
可能值的範圍受不等式 的限制。 *主量子數*
的限制。 *主量子數*  *角動量量子數*
*角動量量子數*  和所謂的 *磁量子數*
和所謂的 *磁量子數*  因此是
因此是

|

|

|

|

|

|
|
|

|

|

|

|

|
|
|

|

|
|
|

|

|

|

|

|
每個可能的量子數集  定義了一個唯一的波函式
定義了一個唯一的波函式  這些波函式共同構成薛定諤方程的束縛態解集(
這些波函式共同構成薛定諤方程的束縛態解集( ),其中
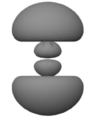
),其中  下面的圖片展示了前三個
下面的圖片展示了前三個  狀態的機率密度分佈情況(未按比例縮放)。它們下方是這些機率密度相對於
狀態的機率密度分佈情況(未按比例縮放)。它們下方是這些機率密度相對於  的分佈圖。可以觀察到,這些狀態具有
的分佈圖。可以觀察到,這些狀態具有  個節點,所有節點都是球形的,即
個節點,所有節點都是球形的,即  為常數的表面。(三維空間中波的節點是二維表面。 “機率波”的節點是
為常數的表面。(三維空間中波的節點是二維表面。 “機率波”的節點是  符號改變的表面,因此機率密度
符號改變的表面,因此機率密度  為零。)
為零。)
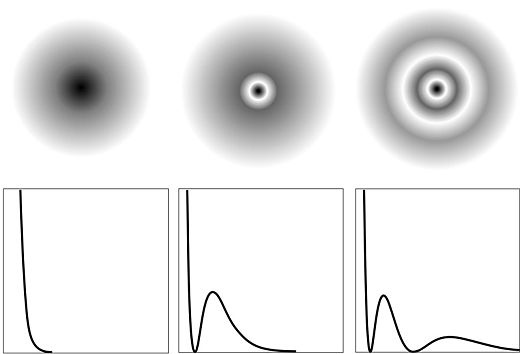
再仔細看看這些圖片。
-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

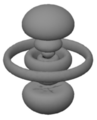
字母 s、p、d、f 分別代表 l=0、1、2、3。 (在理解原子光譜線的量子力學起源之前,人們區分了“銳線”、“主線”、“漫線”和“基線”。這些術語後來被發現對應於  可以取的前四個值。 從
可以取的前四個值。 從  開始,標籤遵循字母表:f、g、h...)。觀察到這些狀態同時顯示球形和圓錐形節點,後者是
開始,標籤遵循字母表:f、g、h...)。觀察到這些狀態同時顯示球形和圓錐形節點,後者是  常數的表面。 (具有
常數的表面。 (具有  的“圓錐形”節點是水平面。) 這些狀態也有總共
的“圓錐形”節點是水平面。) 這些狀態也有總共  個節點,其中
個節點,其中  個是圓錐形的。
個是圓錐形的。
因為  中的“波紋”包含在相位因子
中的“波紋”包含在相位因子  中,它不會出現在
中,它不會出現在  的表示中。 為了使它可見,相位可以用顏色編碼。
的表示中。 為了使它可見,相位可以用顏色編碼。
-

-

-

-

-

-

-

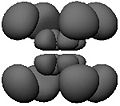
在化學中,通常考慮相反  的真實疊加,如
的真實疊加,如  ,如以下影像所示,它們也是有效的解。
,如以下影像所示,它們也是有效的解。
節點總數再次為  ,非球形節點總數再次為
,非球形節點總數再次為  ,但現在有
,但現在有  個包含
個包含  軸的平面節點和
軸的平面節點和  個錐形節點。
個錐形節點。
為什麼  軸如此特別?其實並沒有什麼特別之處,因為相對於不同軸定義的波函式
軸如此特別?其實並沒有什麼特別之處,因為相對於不同軸定義的波函式  構成了另一組完整的束縛態解。這意味著每個波函式
構成了另一組完整的束縛態解。這意味著每個波函式  可以寫成函式
可以寫成函式  的線性組合,反之亦然。
的線性組合,反之亦然。