量子世界/影響和應用/為什麼能量是量子化的

為什麼能量是量子化的

再次將自己限制在一個空間維度，我們將時間無關薛定諤方程寫成這種形式

${d^{2}\psi (x) \over dx^{2}}=A(x)\,\psi (x),\qquad A(x)={2m \over \hbar ^{2}}{\Big [}V(x)-E{\Big ]}.$

由於該方程除了可能的 $\psi$ 本身之外沒有複數，它有實數解，而我們感興趣的是這些解。你會注意到，如果 $V>E,$ 那麼 $A$ 為正，$\psi (x)$ 與其二階導數具有相同的符號。這意味著 $\psi (x)$ 的圖形在 $x$ 軸上方向上彎曲，在下方向下彎曲。因此它不能穿過軸。另一方面，如果 $V<E,$ 那麼 $A$ 為負，$\psi (x)$ 與其二階導數具有相反的符號。在這種情況下，$\psi (x)$ 的圖形在 $x$ 軸上方向下彎曲，在下方向上彎曲。因此，$\psi (x)$ 的圖形會不斷穿過軸——它是一個波。此外，$E-V,$ 的差越大，圖形的曲率越大；曲率越大，波長越小。在粒子方面，動能越高，動量越大。

現在讓我們找到描述一個粒子“困”在勢阱中的解——束縛態。考慮這個勢

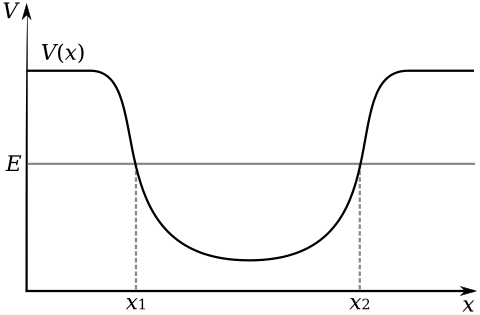
首先觀察到，在 $x_{1}$ 和 $x_{2},$ 處，其中 $E=V,$ $\psi (x)$ 的斜率不會改變，因為在這些點 $d^{2}\psi (x)/dx^{2}=0$。 這告訴我們，在這些點找到粒子的機率不會突然降至零。 因此，有可能在 $x_{1}$ 的左側或 $x_{2},$ 的右側找到粒子，而經典情況下這是不可能的。（經典粒子會在這些點之間來回振盪。）

接下來，考慮由 $\psi (x)$ 定義的機率分佈必須是可歸一的。 對於 $\psi (x)$ 的圖形，這意味著它必須隨著 $x\rightarrow \pm \infty .$ 漸近地逼近 $x$ 軸。

假設我們有一個特定值 $E.$ 的歸一化解。如果我們增加或減少 $E,$ 的值，$\psi (x)$ 影像在 $x_{1}$ 和 $x_{2}$ 之間的曲率會增加或減少。輕微的增加或減少並不會給我們另一個解：$\psi (x)$ 不會在正負 $x.$ 方向上漸近地消失。為了得到另一個解，我們必須將 $E$ 增加正好合適的量，以在“經典”轉折點 $x_{1}$ 和 $x_{2}$ 之間增加或減少一個波節點的數量，並使 $\psi (x)$ 在兩個方向上再次漸近地消失。

底線是，束縛粒子的能量——被“困”在勢阱中的粒子——是量子化的：只有某些值 $E_{k}$ 會產生時間無關薛定諤方程的解 $\psi _{k}(x)$