拓撲/向量空間

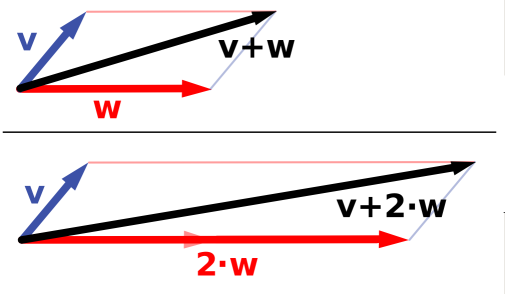
一個向量空間 $V$是由向量的標量倍數形成的。標量通常是實數，但也可以是複數，或者來自任何域。

定義

在一個域 $F$ 上的向量空間 $V$ 是一個集合 $V$，它配備了兩種二元運算： $V$ 元素上的普通向量加法和標量乘法，由 $F$ 的元素對 $V$ 元素進行。這些運算服從 8 個公理（u、v 和 w 是 $V$ 中的向量，a 和 b 是 $F$ 中的標量）

1. 結合律（加法）：(u+v)+w = u+(v+w).

2. 結合律（標量和域乘法）：a(bu) = (ab)u

3. 分配律（域加法）：(a+b)u = au+bu

4. 分配律（向量加法）：a(u+v) = au+av

5. 單位元（加法）：$\exists$ 0 $\in V$ 使得 u+0 = u $\forall$ u $\in V$

6. 單位元（標量乘法）：1u = u

7. 交換律：u+v = v+u

8. 逆元：$\exists$ -u $\in V$ 使得 u+(-u) = 0 $\forall$ u $\in V$

基本箭頭向量的示例：首先是黑色向量作為紅色和藍色向量的和，然後是黑色向量作為藍色向量和紅色向量的縮放（x2）的和。