傳統算盤與珠算/簡介

前言

東方算盤（簡體中文：算盤；繁體中文：算盤；拼音：suànpán，日語： そろばん soroban，在本教科書中簡稱為算盤），作為一種固定珠子在算珠上滑動的算盤，起源於中國，具體日期尚不清楚，但到16世紀後期，算盤的使用完全取代了算籌，成為其母國的一種計算工具。從中國，算盤的使用傳播到其他鄰國，特別是日本、韓國和越南，一直是主要的計算工具，直到現代。算盤的使用方法，“傳統方法”，至少保持了四個世紀的穩定，直到19世紀末，才開始向我們所說的“現代方法”演變，這種方法使用“現代算盤”。本教科書旨在介紹傳統方法，目標讀者是那些已經知道如何使用現代算盤進行現代方法計算的人。

現代算盤與傳統算盤

現代4+1算盤

5+3 和 5+1 算盤

現代算盤是4+1型的，也就是說它在下層有四個算珠，在上層有一個算珠。

4+1 算盤數字表示

	0	1	2	3	4	5	6	7	8	9

這正是能夠用算盤進行十進位制運算所需要的全部。然而，傳統的算盤有額外的算珠，最常見的是5+2型（儘管5+1型在日本也很流行），偶爾也有5+3型。

傳統5+2 中國算盤，展示了懸珠的使用

用三個上層算珠，我們可以在一根算珠上儲存最多20個數字，這對於傳統的除法和乘法技術來說很方便。用兩個上層算珠，我們可以透過使用懸珠技術（懸珠，中文：Xuán zhū，日語：kenshu）來實現同樣的效果，這是一種模擬或虛擬的上層第三個算珠，在需要用到第三個算珠的罕見情況下使用（見圖15到20）。

5+2 算盤數字表示

	0	1	2	3	4	5	5	6	7	8	9	10

	10	11	12	13	14	15	15	16	17	18	19	20

用一個下層第五個算珠，我們有兩種不同的方法來表示數字5、10和15。這意味著我們可以選擇最方便的方法。在加法和減法的情況下，能夠在5和10的兩種表示方法之間進行選擇，將允許我們簡化一些計算。

傳統技術可以應用於任何型別的算盤，只是在4+1算盤上使用下層第五個算珠這一點例外，有沒有額外的上層算珠的區別更多的是舒適度和可靠性問題，而不是效率或能力問題。

現代方法與傳統方法

傳統方法至少使用了四個世紀，涵蓋了中國的明朝和清朝，以及日本的江戶時代。從日本的明治維新開始，學習算盤的學生在學習算盤之前就已經掌握了書面數學，而早期的學生之前對數學一無所知。對於大多數人來說，算盤是他們唯一會學習的數學形式。這就導致了算盤的教學和方法隨著時代和環境的變化而緩慢地適應，在幾十年的時間裡，逐漸形成了我們現在所說的現代方法，事實上，它是一種簡化的方法。

在英語中，下面兩部由高島隆志（Takashi Kojima）撰寫的著作經常被引用，用來參考現代方法

• 《日本算盤：使用方法和理論》（1954）
• 《高階算盤：理論與實踐》（1963）

這兩本書的幾個版本仍然可以找到，包括電子書格式，第一本書可以在archive.org上查閱。在本華夏公益教科書中，假定讀者熟悉這兩本書至少第一本的內容。

今天，現代方法在很多方面似乎是最優的，我們可能會認為傳統方法中的一些“怪異之處”，特別是算盤上除法的組織方式，缺乏實際意義；但如果傳統方法在幾個世紀的時間裡，儘管有數百萬使用者，包括像關孝和這樣的人物，他大力推廣了日本使用算盤，它仍然保持穩定，那麼一定是因為它的使用者也認為它是最優的。只是古人的最優標準與我們今天的標準不同。

不幸的是，過去沒有人費心去寫為什麼事情是這樣做的，他們只寫了如何去做，我們只能推測這些古老技術背後的原因。

傳統方法與現代方法的主要區別

以下三點是傳統技術與現代技術最主要的區別

• 在加法和減法中使用下層第五個算珠，可以略微簡化這兩個操作，這擴充套件到可以用算盤做的一切，因為所有東西最終都依賴於加法和減法。
• 使用除法表進行除法，消除了確定商位所需的腦力勞動。這種方法（kijohou，guīchúfǎ 歸除法）首先由朱世傑（1299）在其《算學啟蒙》中使用算籌進行了描述，取代了舊的基於乘法表的除法方法，該方法的起源可以追溯到公元3到5世紀，即《孫子算經》。這種舊方法，作為書面除法短除法和長除法的基礎，在現代已經取代了傳統的除法方法。也就是說，現代社會又回到了舊方法！
• 傳統方法和現代方法在算盤上組織除法的方式上也存在差異。傳統的除法排列方式比現代的排列方式更加緊湊，但也更加麻煩，因為它需要（或受益於）使用額外的、更高的算珠。這種除法排列方式反過來影響了乘法和開根號的組織方式。

最小努力原則

如上所述，過去的作者都沒有寫過為什麼事情是這樣做的，只寫瞭如何去做；所以我們只能猜測，試圖理解背後的原因。但讀者將在本書中看到，與現代技術相比，傳統技術假設減少了使用算盤所需的腦力勞動。這一點在使用除法表的除法中尤為明顯，在其他將要介紹的技術中也體現出來，因為這些技術有效地減少了完成一項操作所需的“手勢”的數量和/或範圍。我們在這裡所說的手勢是指

• 手指或算珠的動作
• 手部的移動
• 方向的改變
• 跳躍算珠（即，從一個起始算珠改變手部位置到其他非相鄰的算珠）

而每一個手勢，

• 作為一個物理過程，需要時間來完成，
• 由我們的大腦控制，需要我們的注意力，消耗（精神或生化）能量，
• 由人類（而不是機器）完成，有做錯的可能性，從而導致錯誤。

因此，我們可以預期，透過減少這些手勢的數量和範圍，能夠實現更快的、更輕鬆的、更可靠的計算。

鑑於上述情況，人們可能會認為，透過採用這種最小努力原則，傳統技術在使算盤生活更輕鬆的意義上得到了發展，這可以解釋其幾個世紀以來的有效性，但這僅僅是一種沒有文獻支援的推測。

如果我們想到現代方法，它傾向於簡單、速度和效率，我們可以說它是“短跑者方法”，而傳統方法是“馬拉松跑者方法”。

讀者在閱讀完本教材後，將能夠得出自己的結論。

算盤操作表、一些術語和符號

像往常一樣，在本書中，我們將使用表格來描述算盤上的操作，例如

算盤操作表的示例

算盤	註釋
ABCDEFGHIJKLM
896 412	這次除數在左邊，被除數在右邊
896 512	E 列：規則 4/8>5+0，將 E 中的 4 更改為 5，將 0 新增到 F
896 512	無法從 FG 中減去 E×B=5×9=45，
-1	向下修改 E：從 E 中減去 1，
+8	將 8 新增到 F
896 492
等等。	等等。

左邊顯示了算盤狀態的逐位演變，或者顯示了當前的加減運算，以及相關注釋；右邊顯示了正在執行的操作。算盤的列在頂部用字母標記（空白空間表示未使用的/清除的算珠）。

這種表示方法對於現代算盤來說是完美的，但需要進行一些調整以適應傳統算盤。

• 傳統算盤的一列可以包含大於 9 的數字，並且無法在表格中寫入其兩位數字而不會破壞其垂直對齊。為了解決這個問題，我們將對 10 到 19 之間的數字使用“下劃線符號”，第一個數字（1）將用前一列的下劃線表示（請參閱章節 處理溢位 獲取原因）。例如，下面顯示的情況出現在 998001 除以 999 的傳統除法開始不久後

	A	B	C	D	E	F	G	H	I	K	J	L	M
	9	18	9	0	0	1	0	0	0	0	9	9	9

在操作表中表示為

使用下劃線符號

算盤	註釋
ABCDEFGHIJKLM
988001    999	B 列的值為 18

• 

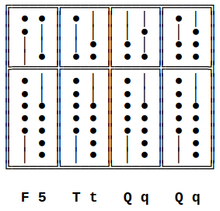
  與使用第五個下珠相關的符號

  如上所示，數字 5、10 和 15 有兩種可能的表示形式：使用或不使用第五個下珠。當需要區分這兩種情況時，我們將使用以下程式碼
  • F： 表示“下五”（啟用五個下珠），與
  • 5： “上五”（啟用一個上珠）相反。
  • T： 一列上的十（啟用一個上珠和五個下珠）。在 5+2 型算盤上，它也是“下十”，與“上十”（啟用兩個上珠）相反。
  • Q： 一列上的“下十五”（啟用兩個上珠和五個下珠），與“上十五”（5+2 型算盤上的懸掛上珠，5+3 型算盤上的三個上珠）相反。

外部資源

算盤訓練器

算盤訓練器展示了一個使用懸掛上珠的 5+2 型算盤。

如果您對傳統技術感興趣，但還沒有傳統算盤，可以使用 JavaScript 應用程式

 Soroban Trainer 

• 您可以在瀏覽器中 直接從 GitHub 執行它
• 或者您可以從 GitHub 上的倉庫 下載到您的計算機上。